时频分析工具箱典型函数的使用

本文全文参考时频特性分析（Matlab），仅仅对文章进行运行测试，整理。
不错的文章
Matlab emd工具箱、时频分析工具箱下载以及安装方法
matlab emd工具箱

特此感谢！

一、概念

法国中央科学研究院和美国RICE大学共同开发了时频分析工具箱（matlab emd）
是一款非常好用的时频分析计算工具，它是分析时变非平稳信号的有力工具，matlab 时频分析工具箱提供了时间域与频率域的联合分布信息，清楚地描述了信号频率随时间变化的关系。
其中主要含有四种函数：

1. 信号产生函数，可以产生不停类型的信号，如Chirp信号，bpsk信号等。
2. 时频分析函数，可以计算线性、Cohen类、仿射类非线性分析值函数，例如短时傅里叶变换（STFT），Gabor变换，谱图，Wigner-Ville（WVD）等。
3. 分析处理函数
4. 图形显示函数，如等高线、三维图等。

二、安装

下载该工具箱，解压到Matlab安装路径下的toolbox文件内，记住这里的路径一会要用。
打开Matlab,在命令窗口输入mex -setup回车，核对是否选择对了编译器。
在命令窗口输入命令pathtool，在弹出的终端窗口添加MATLAB环境变量中。

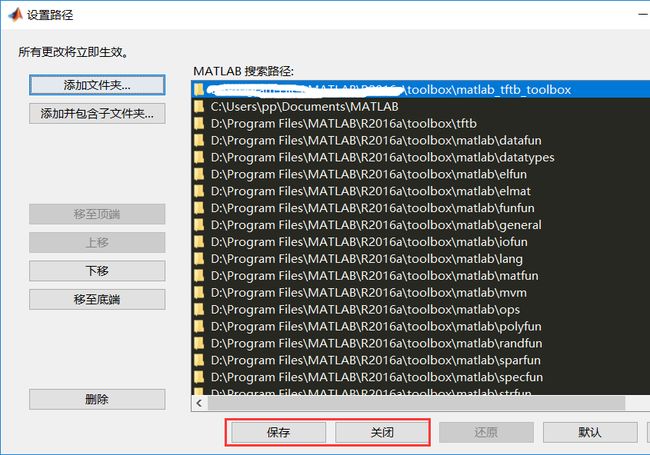
保存后关闭退出。此时即设置生效了。

三、典型函数的使用

AMGAUSS
Generate gaussian amplitude modulation.
Y=AMGAUSS(N,T0,T) generates a gaussian amplitude modulation
centered on a time T0, and with a spread proportional to T.
This modulation is scaled such that Y(T0)=1 and Y(T0+T/2) and Y(T0-T/2) are approximately equal to 0.5 .
产生高斯幅值调制信号，其以信号点数为N，中心为T0，传播0.5的比例到T，即Y(T0)=1，Y(T0+T/2) = Y(T0-T/2) = 0.5。 T0默认为N/2，T默认为2*sqrt(N)。
如：

z=amgauss(160,90,40); 
figure(1)
plot(z);
title('常用产生信号的函数--高斯幅值调制信号');

FMCONST
Signal with constant frequency modulation.
[Y,IFLAW] = FMCONST(N,FNORM,T0) generates a frequency modulation
with a constant frequency fnorm.
The phase of this modulation is such that y(t0)=1.
产生一个固定频率的频率调制信号。N为产生信号的点数，FNORM为标准化频率（默认为0.25），T0表示此时刻为正幅值（默认为round(N/2)），相当于规定了相位。IFLAW为设置的频率变化情况，这里就是一个常数。

```c
z=fmconst(128,0.05,50);
figure(2)
plot(real(z));
title('常用产生信号的函数--固定频率的频率调制信号');

FMLIN
Signal with linear frequency modulation.
[Y,IFLAW]=FMLIN(N,FNORMI,FNORMF,T0) generates a linear frequency modulation.
The phase of this modulation is such that Y(T0)=1.
产生一个线性调频信号。N为信号的点数，FNORMI为开始标准频率（默认为0.0），FNORMF为结束标准频率（默认为0.5），相位由T0规定，即Y(T0)=1。IFLAW为设置的频率变化情况，这里就是一个线性变化的直线。

[z, f]=fmlin(128,0.05,0.3,50); 
figure(3)
subplot(2,1,1)
plot(real(z));
title('常用产生信号的函数--线性调频信号');
subplot(2,1,2);
plot(f)
title('频率变化情况');

一些时频工具箱函数的用法

下面说一些时频分析常用的分析方法，主要有短时傅里叶变换STFT、Wigner-Ville分布WVD、伪Wigner-Ville分布PWVD等，其他还有很多分析方法，都有相关函数，具体可以查看帮助。

功能：计算时间序列的短时离散傅里叶变换，得到瞬时频率。
格式：
[tfr, t, f] = tfrstft(x) % 计算时间序列x的短时傅里叶变换，参数tfr为短时傅里叶变换系数，t为系数tfr对应的时刻，f为归一化频率向量
[tfr, t, f] = tfrstft(x, t) % 计算对应时刻t的短时傅里叶变换
[tfr, t, f] = tfrstft(x, t, n) % 计算n点对应时刻t的短时傅里叶变换
[tfr, t, f] = tfrstft(x, t, n, h) % 参数h为归一化频率平滑窗
[tfr, t, f] = tfrstft(x t, n, h, trace) % trace显示算法进程
说明：
x–信号
t–时间（缺省值为1：length(x))
n–频率数（缺省值为length(x))
h–频率滑窗，h归一化为单位能量（缺省值为hamming（n/4））
trace–如果非零，显示算法的进程（缺省值为0）
tfr–时频分解（为复值），频率轴观察范围为-0.5~0.5
f–归一化频率

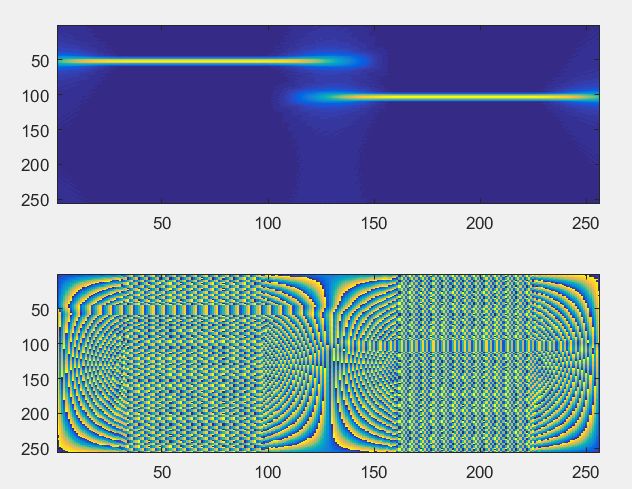
%% 短时傅里叶变换STFT
sig=[fmconst(128,0.2);
fmconst(128,0.4)]; % 产生由两个常值调频信号（即正弦信号）的组合信号
tfr=tfrstft(sig);
subplot(211); imagesc(abs(tfr)); % 瞬时频率
subplot(212); imagesc(angle(tfr)); % 瞬时相位

Wigner-Ville时频分布图
功能：计算时间序列的Wigner-Ville时频分布图，得到瞬时频率
格式：
[tfr, t, f] = tfrwv(x)
[tfr, t, f] = tfrwv(x, t)
[tfr, t, f] = tfrwv(x, t, n)
[tfr, t, f] = tfrwv(x, t, n, trace)
说明：
x–信号
t–时间（缺省值为1：length(x))
n–频率数（缺省值为length(x))
trace–如果非零，显示算法的进程（缺省值为0）
tfr–时频分解（为复值），频率轴观察范围为-0.5~0.5
f–归一化频率

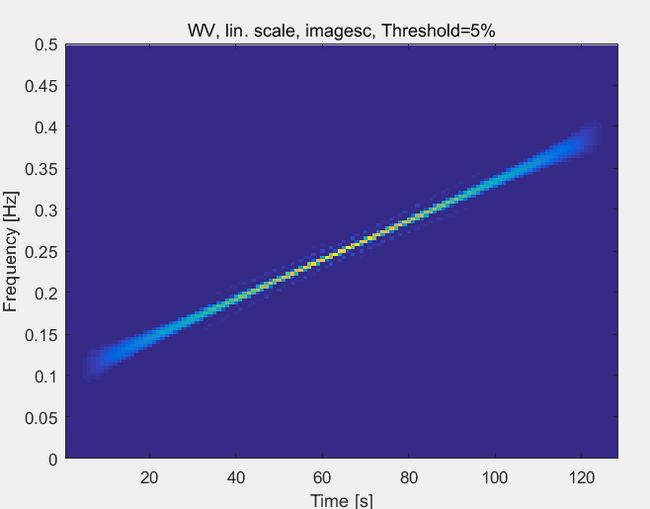
%% Wigner-Ville时频分布图
sig=fmlin(128,0.1,0.4);
figure(333)
tfrwv(sig);

伪Wigner-Ville时频分布图
功能：计算时间序列的伪Wigner-Ville时频分布图，得到瞬时频率
格式：
[tfr, t, f] = tfrpwv(x)
[tfr, t, f] = tfrpwv(x, t)
[tfr, t, f] = tfrpwv(x, t, n)
[tfr, t, f] = tfrpwv(x, t, n, trace)
说明：
x–信号
t–时间（缺省值为1：length(x))
n–频率数（缺省值为length(x))
trace–如果非零，显示算法的进程（缺省值为0）
tfr–时频分解（为复值），频率轴观察范围为-0.5~0.5
f–归一化频率

%% 伪Wigner-Ville时频分布图
sig=fmlin(128,0.1,0.4);
figure()
tfrpwv(sig);

四、一个代码

%---------跳频信号（加入Alpha稳定分布噪声）的FLOSPWV
clear,clc,close all
%--------产生跳频信号
fs=4*10^3;   %采样频率
fk = [1.1 1.3 1.6 1.0 1.7 1.5 1.2 1.4]*10^3;   %跳频图案集
th=50*10^(-3);   %跳频周期，每跳驻留时间

ze = zeros(1,0);   %0表示信号延迟为零
x = []; sig = ze;
t = 0:1/fs:th-1/fs;
for i = fk;
    x = cos(2*pi*i*t);
    sig = [sig x];   %sig为输出跳频信号
end

N = length(sig);


%-------------加入Alpha稳定分布噪声
U=unifrnd(-pi/2,pi/2,1,1600);
W=exprnd(1,1,1600);

alpha=0.8;

X=(sin(alpha*U)./cos(U).^(1/alpha)).*(cos(U-alpha*U)./W).^((1-alpha)/alpha); %产生Alpha稳定分布

m=3;   %信噪比，单位为dB

sig_temp=sig.*(10.^m/20)./std(sig);   %根据信噪比重新调整信号幅度

sig=sig_temp+X;


%----------低阶spwv分析
 p=0.2; 
 flosig=abs(sig).^p.*sign(sig);  %直接在信号上作低阶改变，使用原toolbox 
 sa=hilbert(flosig);
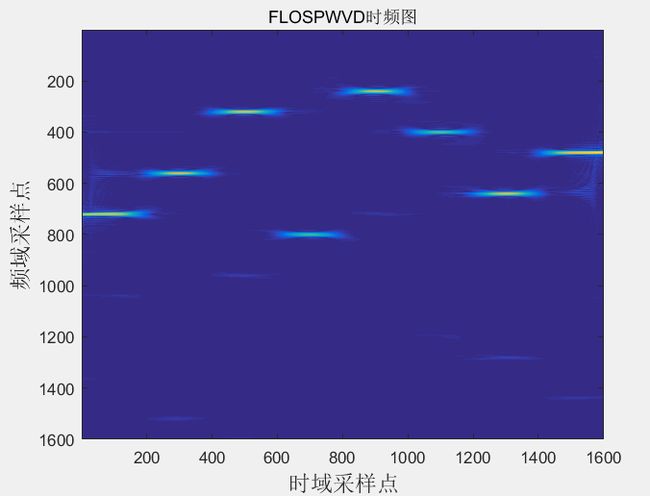
[tfr,t,f]=tfrspwv(sa');
imagesc(abs(tfr));
title('FLOSPWVD时频图');
xlabel('时域采样点','fontsize',14);
ylabel('频域采样点','fontsize',14);

效果：