数字信号处理课程中基于matlab的低通滤波器的设计
数字信号处理课程中基于matlab的低通滤波器的设计
1.实验要求
在Matlab中绘制以下信号: x(t)= sin(20* pi * t) + sin(200 *pi * t);
要求:
- 采样频率是信号上限频率的4-6倍或更高,绘制x(t)的波形图,至少画出两个周期;
- 利用FFT,绘制x(t)的频谱图(幅度谱),要求横坐标是物理频率(0-fs Hz);
- 要求设计一个通带平坦 的IIR低通滤波器,通带和阻带边界频率及衰减可自己设定,设计满足要求的模拟滤波器,分别用脉冲响应不变法和双线性变换法转换成数字滤波器,画出滤波器的幅频特性和相频特性,最后对x(t)滤波,分析滤波后信号的频率特性;
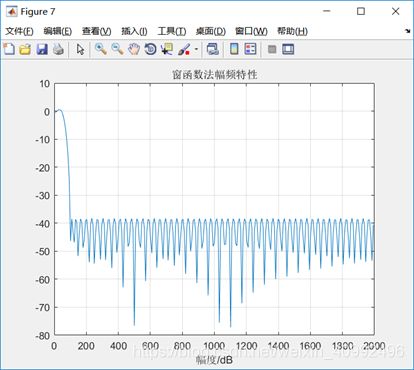
- 要求用窗函数法设计一个FIR低通滤波器,阻带最小衰减约50dB,画出滤波器的幅频特性和相频特性,最后对x(t)滤波,分析滤波后信号的频率特性;
2.实验代码
%实验一
x(t)的波形图
fs=1000;%采样频率
N=500; %采样点数
n=0:N-1;% 采样序列
t=n/fs; % 时间序列
x=sin(20*pi*t)+sin(200*pi*t);
figure(1);
subplot(2,1,1);
plot(x);%画图函数
title('x(t)时域图形');
xlabel('n');
ylabel('x');
grid;%打开网格
%实验二
x(t)的频谱图
clear all;
Fs=1000;
N = 500; % 采样点数
n = 0:N-1; % 采样序列
t = 0:1/Fs:1-1/Fs; % 时间序列
f = (0:N-1) * Fs / N;
%真实的频率
x=sin(20*pi*t)+sin(200*pi*t);%原始信号
y = fft(x, N); %对原始信号做 FFT 变换
Mag = abs(y); %求 FFT
转换结果的模值
figure(1);
subplot(2,1,2);
plot(f, Mag); %绘制幅频相应曲线
title('fft 幅频相应');
xlabel('频率/Hz');
ylabel('幅度');
%实验三 用脉冲响应法设计IIR低通滤波器
clear all;
fp=50;
fs=100;
Rp=4;
Rs=50;
Fs=1000;
Wp=2*pi*fp;
Ws=2*pi*fs; %设置归一化通带和阻带截止频率
Nn=256;
n=(0:500-1); %采样点数
[N,Wn]=buttord(Wp,Ws,Rp,Rs,'s');%调用butter函数确定巴特沃斯滤波器阶数
[b,a]=butter(N,Wn,'s'); %调用butter函数设计巴特沃斯滤波器
w=linspace(1,400,100)*2*pi; %指定一段频率值
H=freqs(b,a,w); % 在[0,2π]上进行采样,采样频率点由矢量w指定
figure(2);
plot(w/(2*pi),20*log10(abs(H)));
%绘出巴特沃斯模拟滤波器的幅频特性曲线
title('巴特沃斯模拟滤波器幅频特性');
xlabel('频率/Hz');
ylabel('幅度/db');
[bz,az]=impinvar(b,a,Fs); %调用脉冲响应不变法
figure(3);
subplot(2,1,1);
freqz(bz,az,Nn,Fs);% 对H(ejω)在[0,Fs/2]上等间隔采样Nn点
grid on;
title('巴特沃斯数字滤波器幅频特性'); %绘出巴特沃斯数字低通滤波器的幅频特性曲线
xlabel('幅度/Hz');ylabel('频率/db');
subplot(2,1,2);
title('巴特沃斯数字滤波器相频特性'); %绘出巴特沃斯数字低通滤波器的相频特性曲线
xlabel('幅度/Hz');ylabel('频率/db');
grid on;
figure(4);
subplot(2,1,1);
x=sin(20*pi*n/Fs)+sin(200*pi*n/Fs);
plot(n,x);
title('脉冲响应法滤波前输入信号图像');
xlabel('时间(s)');
ylabel('幅值');
grid on;
figure(4);
subplot(2,1,2);
y=filter(bz,az,x);%对原信号进行滤波¨
plot(n/fs,y);
title('脉冲响应法滤波后输入信号图像');
xlabel('时间(s)');
ylabel('幅值');
%实验三 双线性变换法设计IIR低通滤波器
clear all;
fp=50;
fs=100;
Rs=50;
Fs=1000;
Rp=3;
Ts=1/Fs;
n=(0:500-1);
wp=2*pi*fp; %利用
ws=2*pi*fs;
[N,Wn]=buttord(wp,ws,Rp,Rs,'s');%选择滤波器的最小阶数
[Z,P,K]=buttap(N); %创建butterworth模拟滤波器
[Bap,Aap]=zp2tf(Z,P,K); %把滤波器零极点模型转化为传递函数模型
[b,a]=lp2lp(Bap,Aap,Wn);%把模拟滤波器原型转换成截至频率为Wn的低通滤波器
[bz,az]=bilinear(b,a,Fs);%用双线性变换法实现模拟滤波器到数字滤波器的转换
[H,W]=freqz(bz,az); %绘制频率响应曲线
figure(5);
plot(W*Fs/(2*pi),abs(H));
grid
title('双线性变换法幅频特性');
xlabel('频率/Hz')
ylabel('幅度')
figure(6);
subplot(2,1,1);
x=sin(20*pi*n/Fs)+sin(200*pi*n/Fs);
plot(n,x);
title('双线性变换法滤波前输入信号图像');
xlabel('时间(s)');
ylabel('幅值');
grid on;
subplot(2,1,2);
y=filter(bz,az,x);%对原信号进行滤波¨
plot(n/fs,y);
title('双线性变换法滤波后输入信号图像');
xlabel('时间(s)');
ylabel('幅值');
%实验四 窗函数法设计一个FIR低通滤波器
clear all;
Fs=1000; %图像的采样频率
n=(0:500-1);%采样点
fedge=[50 100];%通带和阻带边界频率
mval=[1 0];%通带和阻带边界处幅值
dev=[0.0559 0.01];%通带和阻带的波动
fs=4000;%采样频率
[N,fpts,mag,wt]=remezord(fedge,mval,dev,fs);
b=remez(N,fpts,mag,wt);
[h,w]=freqz(b,1,256);
figure(7);
plot(w*2000/pi,20*log10(abs(h)));
grid;
title('窗函数法幅频特性');
xlabel('频率/Hz');
xlabel('幅度/dB');
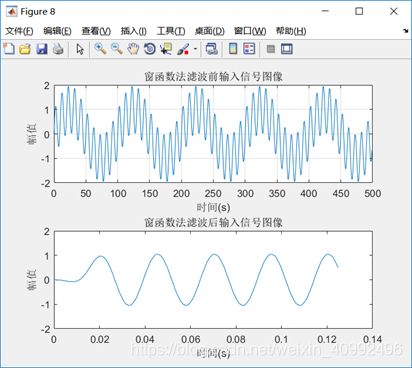
figure(8);
subplot(2,1,1);
x=sin(20*pi*n/Fs)+sin(200*pi*n/Fs);
plot(n,x);
title('窗函数法滤波前输入信号图像');
xlabel('时间(s)');
ylabel('幅值');
grid on;
subplot(2,1,2);
y=fftfilt(b,x);%对原信号进行滤波,FIR滤波器中调用滤波函数与IIR不同。
plot(n/fs,y);
title('窗函数法滤波后输入信号图像');
xlabel('时间(s)');
ylabel('幅值');
带尺寸的图片: 3.实验结果
①采样频率是信号上限频率的4-6倍或更高,绘制x(t)的波形图,至少画出两个周期;
②利用FFT,绘制x(t)的频谱图(幅度谱),要求横坐标是物理频率(0-fs Hz);
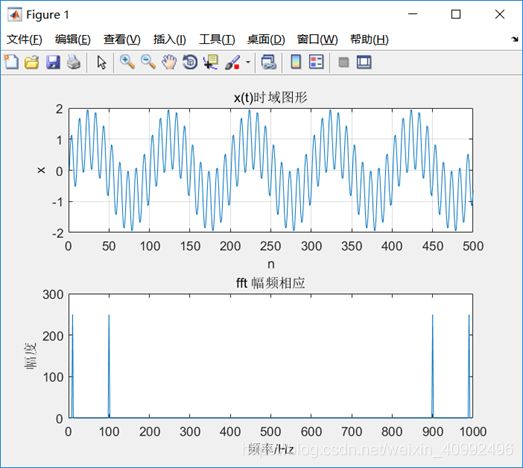
3.要求设计一个通带平坦 的IIR低通滤波器,通带和阻带边界频率及衰减可自己设定,设计满足要求的模拟滤波器,分别用脉冲响应不变法和双线性变换法转换成数字滤波器,画出滤波器的幅频特性和相频特性,最后对x(t)滤波,分析滤波后信号的频率特性;
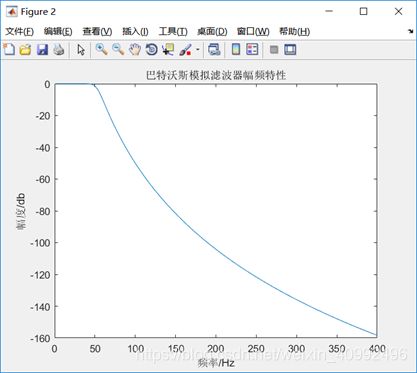
I.脉冲响应不变法
本实验通过设计一巴特沃斯模拟滤波器,后设计数字滤波器完成;
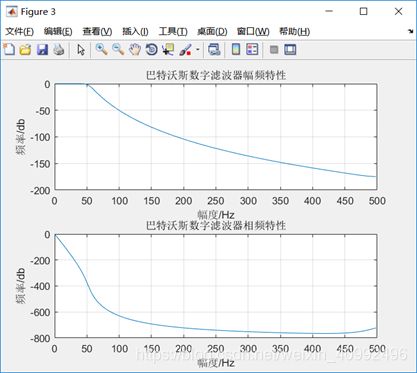

II.双线性变换法

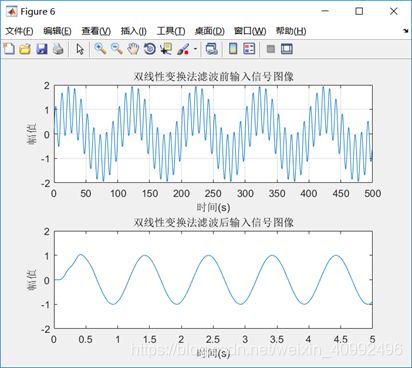
④要求用窗函数法设计一个FIR低通滤波器,阻带最小衰减约50dB,画出滤波器的幅频特性和相频特性,最后对x(t)滤波,分析滤波后信号的频率特性;
本实验利用雷米兹算法设计滤波器;
有不对的地方欢迎大家批评指正。