数据压缩（十二）——matlab傅里叶变换仿真分析和《完全重建QMF滤波器组的设计》阅读

---

任务1：仿真分析两种波形的傅里叶变换，一个在序列前端有值，一个在序列后端有值
任务2：跑一遍完全重建QMF滤波器组的代码，了解其背后流程

一、MATLAB傅里叶变换仿真分析

1.1 matlab代码

x1=[0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0];
x2=[0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0];
Y1=fft(x1);
figure(1);
subplot(2,1,1);
stem(abs(Y1));
title("Y1幅度谱");
subplot(2,1,2);
stem(angle(Y1)/pi*180);
title("Y1相位谱");
figure(2);
Y2=fft(x2);
subplot(2,1,1);
stem(abs(Y2));
title("Y2幅度谱");
subplot(2,1,2);
stem(angle(Y2)/pi*180);
title("Y2相位谱");

x3=[0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1];
Y3=fft(x3);
figure(3);
subplot(2,1,1);
stem(abs(Y3));
title("Y3幅度谱");
subplot(2,1,2);
stem(angle(Y3)/pi*180);
title("Y3相位谱");

1.2 结果

[0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0]	[0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0]	[0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]

1.3 结果分析

可以发现：

1. 时域波形窄，频域波形宽；时域波形宽，频域波形窄。
2. 时域移位后，频域的幅度谱不变，只有相位谱发生改变。

二、《完全重建QMF滤波器组的设计》

2.1 完全重建QMF滤波器组

  完全重建QMF滤波器组最大的优点是在对信号进行抽取后，可以根据每个子带的不同特征分别进行处理。
完全重建QMF滤波器组的设计：

• 特征值法
• 最小二乘法
• 遗传法
• 多项式分解法
    这些方法的缺点：计算复杂，参数不容易确定，程序编写较难。

2.2 两通道正交镜像滤波器组理论

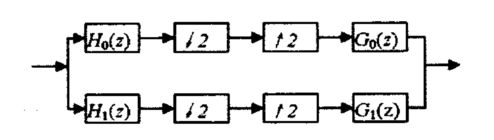
  在分析滤波器组一侧，输入信号被分为k个子频带信号，通过抽取降低采样率；在综合滤波器一侧，通过零值内插和带通滤波重建原来的信号。
  综合滤波器组最后输出的信号$\hat{x}(n{T}_1)$与分析滤波器组原来输入的信号$x(n{T}_1)$有如下关系：$$\hat{x}(n{T}_1)=cx[(n-n_0)T_1]$$
  称$\hat{x}(n{T}_1)$是对$x(n{T}_1)$的完全重建。
这两者之间存在着误差：

• 混叠失真【由抽取和内插产生的混叠和镜像带来的误差，导致分析滤波器组和综合滤波器组的频带不能完全分开】
• 幅度失真【由于分析和综合滤波器组的频带在通带内不是全通函数，其幅频特性波纹产生的误差】
• 相位失真【由滤波器相频特性的非线性所产生的误差】
• 量化失真【由编、解码产生的误差，与量化噪声相似，这类误差无法完全消除，只能设法减小】

消除混叠失真：
  令：$$\begin{array}{rl}{G}_0(z)=& H_0(z)\\ G_1(z)=& -H_1(z)=-H_0(-z)\end{array}$$  若$H_0(z)$是一个低通滤波器，$H_1(z),G_0(z),G_1(z)$则分别是高通、低通、高通滤波器。

2.3 完全重建QMFB遇到的问题和解决方法

  完全重建是目的，但是滤波器组的核心作用是子带分解【因为做不到QMFB的完全重建】
解决方法：

1. 用FIR QMF滤波器组，去除相位失真的前提下，尽可能的减小幅度失真，近似实现完全重建
2. 用IIR QMF滤波器组，去除幅度失真，不考虑相位失真，近似实现完全重建
3. 修正QMF滤波器的关系，去考虑更合理的形式，从而实现完全重建

2.4 完全重建QMFB的设计

  只需要知道各滤波器的阶数$N$和滤波器的通带截止频率$\omega$，就可以得到完全重建QMFB的分析、综合滤波器组的时域形式$h_0,h_1,g_0,g_1$，误差较小且能达到良好的精度。其中，$N$必须为奇数，$\omega$必须小于0.5。
  找$N$和$\omega$是通过求出均方误差MSE进行比较得到的。

确定N值和w值

  通过MSE的比较，最终得到最优的$N$值和$\omega$值是$N=41,\omega =0.43$

matlab代码

N=41;
w=0.43;
[h0,h1,g0,g1]=firpr2chfb(N,w);
[H1z,w]=freqz(h0,1,512);
H1_abs=abs(H1z);H1_db=20*log10(H1_abs);
[H2z,w]=freqz(h1,1,512);
H2_abs=abs(H2z);H2_db=20*log10(H2_abs);
%%%%%%%%%%滤波器h0和h1的幅度响应%%%%%%%%%%
figure(1); 
plot(w/pi,H1_db,'-',w/pi,H2_db,'--'); 
axis([0,1,-100,10]); 
grid 
xlabel('\omega/\pi');ylabel('幅度,dB'); 
sum1=H1_abs.*H1_abs+H2_abs.*H2_abs; 
d=10*log10(sum1);
%%%%%%%%%%%%幅度响应关系误差%%%%%%%%%%%%%
figure(2) 
plot(w/pi,d);grid; 
xlabel('\omega/\pi');ylabel('误差,dB'); 
axis([0,1,-0.04,0.04]); 
%%%%%%%%%%%%%x1(n)%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,500);
x(2)=1;x(3)=1;
x(6)=2;x(7)=2;x(8)=2;
x(17)=1.5;x(18)=1.5;x(19)=1.5;
x(24)=1;x(25)=1;
x(33)=3;x(34)=3;x(35)=3;
%%%%%%%%%%%%%%x2(n)%%%%%%%%%%%%%%%%%%%%
x=zeros(1,500);
x(1)=1;x(2)=1;x(3)=1;
x(9)=2;x(10)=2;x(11)=2;
x(16)=3;x(17)=3;x(18)=3;
x(24)=4;x(25)=4;x(26)=4;
x(33)=3;x(34)=3;x(35)=3;
x(41)=2;x(42)=2;x(43)=2;
x(49)=1;x(50)=1;x(51)=1;
%%%%%%%%%%%%%%x3(n)%%%%%%%%%%%%%%%%%%%%
n=1:500;
T=0.2;
x=sin(n*T);
hlp=mfilt.firdecim(2,h0);
hhp=mfilt.firdecim(2,h1);
glp=mfilt.firinterp(2,g0);
ghp=mfilt.firinterp(2,g1);
x0=filter(hlp,x);
x0=filter(glp,x0);
x1=filter(hhp,x);
x1=filter(ghp,x1);
xidle=x0+x1;
xshift=[zeros(1,N) x(1:end-N)];
e=xidle-xshift;
mes=sum(abs(e).^2)/length(e)
fvtool(h0)
%%%%%%%%%%%%输入信号%%%%%%%%%%%%%%%%%%
figure(4);
plot(x);
%%%%%%%%%%理想输出信号与重建输出信号%%%%%%%
figure(5);
axis([0,500,-1,1]); 
plot(xshift,'r');hold on;
plot(xidle,'-');
axis([0,600,-1.1,1.1]);
%%%%%%%理想输出信号与重建输出信号的偏差%%%%%%
%%理想输出信号与重建的输出信号的偏差
figure(6);
plot(xshift-xidle);

  程序中firpr2chfb是直接根据参数来设计完全重建滤波器的函数【Two-channel FIR filter bank for perfect rec truction】

【结果】滤波器$H_0(z)$和$H_1(z)$的幅度响应

  这两个幅度响应加起来占满了整个通道，也就是这两个滤波器对原来的频带进行了子带分解。
  同时，这两个滤波器是镜像对称的。

【结果】幅度响应关系误差

  可以发现，误差很小，在0.01的数量级上，几乎可以忽略不记。

【结果】输入信号&理想输出信号（红色线）与重建的输出信号（蓝色线）

输入信号	理想输出信号（红色线）与重建的输出信号（蓝色线）

  可以发现，在本实验中，输出信号只是输入信号的时移。并没有对幅度进行调整。

【结果】理想输出信号与重建输出信号的偏差

  可以发现，理想输出信号与重建输出信号的偏差相对较小【数量级为$10^{-5}$】，因此，可以实现QMFB的近似完全重建。

【结果】$h_0$的幅度响应

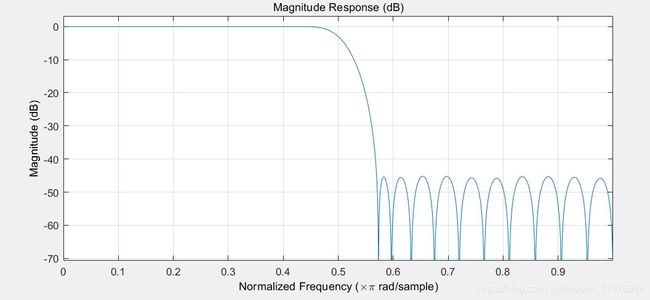
  可以发现，$h_0$的通带基本等同于一条直线，并且过渡带也很窄，阻带的最大值也是-70db，完全可以满足要求。
  所以设计出来的$h_0$的幅度响应近似于理想。

2.5 结论

  用matlab实现完全重建QMFB的设计，非常简单【只需要使用firpr2chfb函数】极大地减轻了工作量，得到的均方误差也较小，具有相对较高的精度，最优参数一般可以选取N=41，=0.43。