SEAL库 例2之encodes.cpp解析

在“1 _bfv_basics。我们展示了如何使用BFV方案执行一个非常简单的计算。计算以明文模为参数，仅利用一个BFV明文多项式的系数。这种方法有两个值得注意的问题:

   (1)实际应用中一般采用整数或实数算法，而不是模运算;

   (2)我们只使用了明文多项式的一个系数。这是非常浪费的，因为明文多项式很大，而且在任何情况下都将全部加密。

对于(1)，有人可能会问，为什么不直接增加plain_modules参数，直到没有溢出发生，并且计算的行为就像整数算术一样。问题是增加plain_module会增加噪声预算消耗，同时降低初始噪声预算。

在这些示例中，我们将讨论将数据放入明文元素(编码)的其他方法，这些方法允许进行更多的计算，而不会出现数据类型溢出，并且允许使用完整的明文多项式。

IntegerEncoder

void example_integer_encoder()

IntegerEncoder将整数编码为BFV明文多项式，如下所示。首先，计算整数的二进制展开。接下来，创建一个以位作为系数的多项式。例如，整数

26 = 2^4 + 2^3 + 2^1`

被编码成多项式

1x^4 + 1x^3 + 1x^1

相反地，明文多项式是通过在x=2处取值来解码的。对于负数，IntegerEncoder只将所有系数存储为0或-1，其中-1由内存中的无符号整数plain -1表示。

由于加密计算是在多项式上进行的，而不是在经过编码的整数本身上进行的，因此多项式系数将在这样的计算过程中增长。例如，计算加密后的整数26与自身的和，将得到系数较大的加密多项式:

2x^4 + 2x^3 + 2x^1

。将经过加密的整数26平方也会由于交叉项导致系数增加，即

(1 x ^ 4 + 1 x ^ 3 + 1 x ^ 1) ^ 2 = 1 x ^ 8 + 2 x ^ 7 + 1 x ^ 6 + 2 x ^ 5 + 2 x ^ 4 + 1 x ^ 2;

进一步的计算将迅速增加更多的系数。解码在这种情况下仍然可以正常工作(对多项式求值)。但由于明文多项式的系数实际上是整数模素模，隐式约简模素模产生意想不到的结果。例如，将1x^4 + 1x^3 + 1x^1多次与自身的素模相加将得到常数多项式0，它显然不等于26 *素模。很难预测何时会发生这种溢出，尤其是在计算多个顺序乘法时。IntegerEncoder易于理解和用于简单的计算，对于刚接触微软印章的用户来说，它是一个很好的实验工具。然而，高级用户可能更喜欢更有效的方法，如BatchEncoder或CKKSEncoder。

EncryptionParameters parms(scheme_type::BFV);
size_t poly_modulus_degree = 4096;
parms.set_poly_modulus_degree(poly_modulus_degree);
parms.set_coeff_modulus(CoeffModulus::BFVDefault(poly_modulus_degree));

在我们选择plain_modules的背后没有隐藏的逻辑。唯一的重要的是明文多项式系数不会 在计算过程中，在任何时刻超过该值;否则结果将是不正确的。

parms.set_plain_modulus(512);
auto context = SEALContext::Create(parms);
print_parameters(context);
cout << endl;

KeyGenerator keygen(context);
PublicKey public_key = keygen.public_key();
SecretKey secret_key = keygen.secret_key();
Encryptor encryptor(context, public_key);
Evaluator evaluator(context);
Decryptor decryptor(context, secret_key);

We create an IntegerEncoder.

首先，我们将两个整数编码为明文多项式。注意，编码不是加密:在这一点上没有加密。

int value1 = 5;
Plaintext plain1 = encoder.encode(value1);
print_line(__LINE__);
cout << "Encode " << value1 << " as polynomial " << plain1.to_string()
    << " (plain1)," << endl;

int value2 = -7;
Plaintext plain2 = encoder.encode(value2);
cout << string(13, ' ') << "encode " << value2 << " as polynomial " << plain2.to_string()
    << " (plain2)." << endl;

Now we can encrypt the plaintext polynomials.

Ciphertext encrypted1, encrypted2;
print_line(__LINE__);
cout << "Encrypt plain1 to encrypted1 and plain2 to encrypted2." << endl;
encryptor.encrypt(plain1, encrypted1);
encryptor.encrypt(plain2, encrypted2);
cout << "    + Noise budget in encrypted1: "
    << decryptor.invariant_noise_budget(encrypted1) << " bits" << endl;
cout << "    + Noise budget in encrypted2: "
    << decryptor.invariant_noise_budget(encrypted2) << " bits" << endl;

As a simple example, we compute (-encrypted1 + encrypted2) * encrypted2.

encryptor.encrypt(plain2, encrypted2);
Ciphertext encrypted_result;
print_line(__LINE__);
cout << "Compute encrypted_result = (-encrypted1 + encrypted2) * encrypted2." << endl;
evaluator.negate(encrypted1, encrypted_result);//这是一个负门操作，存入encrypted_result
evaluator.add_inplace(encrypted_result, encrypted2); //内置加门操作，存入encrypted_result
evaluator.multiply_inplace(encrypted_result, encrypted2);//内置乘门操作，存入encrypted_result
cout << "    + Noise budget in encrypted_result: "
    << decryptor.invariant_noise_budget(encrypted_result) << " bits" << endl;
Plaintext plain_result;
print_line(__LINE__);
cout << "Decrypt encrypted_result to plain_result." << endl;
decryptor.decrypt(encrypted_result, plain_result);  //解密，存入plain_result

打印结果明文多项式。系数甚至不接近超过我门的明文模数，512。

cout << "    + Plaintext polynomial: " << plain_result.to_string() << endl;

    //Decode to obtain an integer result.
    print_line(__LINE__);
    cout << "Decode plain_result." << endl;
    cout << "    + Decoded integer: " << encoder.decode_int32(plain_result);
    cout << "...... Correct." << endl;
}

BatchEncoder

void example_batch_encoder()
{
    print_example_banner("Example: Encoders / Batch Encoder");

设N为poly_modulus_degree，T为plain_modulus。批处理允许BFV明文多项式被视为2×(N/2)矩阵，每个元素都是一个模T整数。在矩阵视图中，加密操作在加密矩阵上逐个执行element-wise，允许用户在完全向量化计算中获得几个数量级的速度提升。因此，除了最简单的计算之外，批处理应该是首选的方法。使用BFV时，如果使用得当，实现的性能将超过使用IntegerEncoder完成的任何工作。

EncryptionParameters parms(scheme_type::BFV);
size_t poly_modulus_degree = 8192;
parms.set_poly_modulus_degree(poly_modulus_degree);
parms.set_coeff_modulus(CoeffModulus::BFVDefault(poly_modulus_degree));

为了启用批处理，我们需要将plain_modules设置为一个素数，它全等于1模2*poly_modulus_degree。（这里是指要求素数满足的条件）。Microsoft SEAL提供了一种辅助方法来查找这样的素数。在本例中，我们创建了一个支持批处理的20位素数。

parms.set_plain_modulus(PlainModulus::Batching(poly_modulus_degree, 20));
auto context = SEALContext::Create(parms);
print_parameters(context);
cout << endl;

我们可以通过查看由SEALContext创建的加密参数限定符来验证是否确实启用了批处理。

auto qualifiers = context->first_context_data()->qualifiers();
cout << "Batching enabled: " << boolalpha << qualifiers.using_batching << endl;

KeyGenerator keygen(context);
PublicKey public_key = keygen.public_key();
SecretKey secret_key = keygen.secret_key();
RelinKeys relin_keys = keygen.relin_keys();
Encryptor encryptor(context, public_key);
Evaluator evaluator(context);
Decryptor decryptor(context, secret_key);

Batching is done through an instance of the BatchEncoder class.

BatchEncoder batch_encoder(context);

批处理“槽slot”的总数等于poly_modulus_degree, N，这些槽被组织成2×(N/2)矩阵，可以对其进行加密和计算。每个槽都包含一个整数 modulo plain_modulus。

size_t slot_count = batch_encoder.slot_count();
size_t row_size = slot_count / 2;
cout << "Plaintext matrix row size: " << row_size << endl;

矩阵明文被简单地作为一个扁平的向量提供给BatchEncoder 的数字。第一 row_size 多的数字组成第一行，其余的组成第二行。这里我们创建以下矩阵:

    [ 0,  1,  2,  3,  0,  0, ...,  0 ]
    [ 4,  5,  6,  7,  0,  0, ...,  0 ]、

    vector<uint64_t> pod_matrix(slot_count, 0ULL);
    pod_matrix[0] = 0ULL;
    pod_matrix[1] = 1ULL;
    pod_matrix[2] = 2ULL;
    pod_matrix[3] = 3ULL;
    pod_matrix[row_size] = 4ULL;
    pod_matrix[row_size + 1] = 5ULL;
    pod_matrix[row_size + 2] = 6ULL;
    pod_matrix[row_size + 3] = 7ULL;

    cout << "Input plaintext matrix:" << endl;
    print_matrix(pod_matrix, row_size);

First we use BatchEncoder to encode the matrix into a plaintext polynomial.

Plaintext plain_matrix;
print_line(__LINE__);
cout << "Encode plaintext matrix:" << endl;
batch_encoder.encode(pod_matrix, plain_matrix);

我们可以立即解码，以验证编码的正确性。注意，还没有进行加密或解密。

vector<uint64_t> pod_result;
cout << "    + Decode plaintext matrix ...... Correct." << endl;
batch_encoder.decode(plain_matrix, pod_result);
print_matrix(pod_result, row_size);

Next we encrypt the encoded plaintext.

   Ciphertext encrypted_matrix;
    print_line(__LINE__);
    cout << "Encrypt plain_matrix to encrypted_matrix." << endl;
    encryptor.encrypt(plain_matrix, encrypted_matrix);
    cout << "    + Noise budget in encrypted_matrix: "
        << decryptor.invariant_noise_budget(encrypted_matrix) << " bits" << endl;

对密文的操作导致在所有8192个槽(矩阵元素)中同时执行同态操作。为了说明这一点，我们构造了另一个明文矩阵：

    [ 1,  2,  1,  2,  1,  2, ..., 2 ]
    [ 1,  2,  1,  2,  1,  2, ..., 2 ]          并将其编码为明文。

 vector<uint64_t> pod_matrix2;
for (size_t i = 0; i < slot_count; i++)
{
    pod_matrix2.push_back((i % 2) + 1);
}
Plaintext plain_matrix2;
batch_encoder.encode(pod_matrix2, plain_matrix2);
cout << endl;
cout << "Second input plaintext matrix:" << endl;
print_matrix(pod_matrix2, row_size);

现在，我们将第二个(明文)矩阵添加到加密矩阵中，并将其平方

 print_line(__LINE__);
cout << "Sum, square, and relinearize." << endl;
evaluator.add_plain_inplace(encrypted_matrix, plain_matrix2);
evaluator.square_inplace(encrypted_matrix);
evaluator.relinearize_inplace(encrypted_matrix, relin_keys);

How much noise budget do we have left?

   cout << "    + Noise budget in result: "
        << decryptor.invariant_noise_budget(encrypted_matrix) << " bits" << endl;

We decrypt and decompose the plaintext to recover the result as a matrix.

    Plaintext plain_result;
    print_line(__LINE__);
    cout << "Decrypt and decode result." << endl;
    decryptor.decrypt(encrypted_matrix, plain_result);
    batch_encoder.decode(plain_result, pod_result);
    cout << "    + Result plaintext matrix ...... Correct." << endl;
    print_matrix(pod_result, row_size);

当所需的加密计算高度可并行化时，批处理允许我们有效地使用全明文多项式。但是，它并没有解决这个文件开头提到的另一个问题:每个槽只包含一个整数模的明文模量，除非明文模量非常大，否则我们可以很快遇到数据类型溢出，并在需要整数计算时会得到意外的结果。注意，溢出并不能以加密的形式检测到。CKKS方案(以及CKKSEncoder)解决了数据类型溢出问题，但代价是只产生近似的结果。

void example_ckks_encoder()

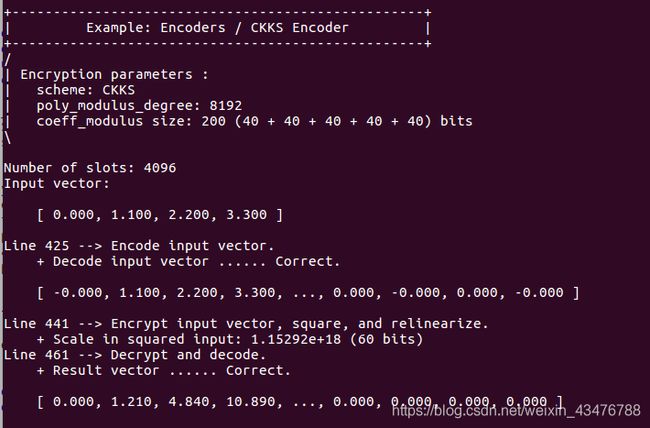
print_example_banner("Example: Encoders / CKKS Encoder");

CKKSEncoder在本例中，我们演示了用于计算加密的实数或复数的Cheon-Kim-Kim-Song
(CKKS)方案。我们首先为CKKS方案创建加密参数。与BFV方案相比，有两个重要的区别:

(1) CKKS不使用明文模数加密参数;

(2)在使用CKKS方案时，以特定的方式选择coeff_modules是非常重要的。我们将在“ckks_basic.cpp”文件中进一步解释这一点。在这个例子中，我们使用CoeffModulus::Create来生成5个40位素数。

    EncryptionParameters parms(scheme_type::CKKS);
    size_t poly_modulus_degree = 8192;
    parms.set_poly_modulus_degree(poly_modulus_degree);
    parms.set_coeff_modulus(CoeffModulus::Create(
        poly_modulus_degree, { 40, 40, 40, 40, 40 }));

We create the SEALContext as usual and print the parameters.

auto context = SEALContext::Create(parms);
print_parameters(context);
cout << endl;

/*
Keys are created the same way as for the BFV scheme.
*/
KeyGenerator keygen(context);
auto public_key = keygen.public_key();
auto secret_key = keygen.secret_key();
auto relin_keys = keygen.relin_keys();

/*
We also set up an Encryptor, Evaluator, and Decryptor as usual.
*/
Encryptor encryptor(context, public_key);
Evaluator evaluator(context);
Decryptor decryptor(context, secret_key);

要创建CKKS明文，我们需要一个特殊的编码器:没有其他方法可以创建它们。IntegerEncoder和BatchEncoder不能与CKKS方案一起使用。CKKSEncoder将实数或复数的向量编码成明文对象Plaintext objects，这些对象随后可以被加密。在高层次上，这看起来很像BatchEncoder为BFV方案所做的，但是它背后的理论是完全不同的。

  CKKSEncoder encoder(context);

在CKKS中，槽的数量是poly_modulus_degree / 2，每个槽编码一个实数或复数。这应该与BFV方案中的BatchEncoder形成对比，在BFV方案中，槽的数量等于poly_modulus_degree，它们被排列成两行的矩阵。

 size_t slot_count = encoder.slot_count();
    cout << "Number of slots: " << slot_count << endl;

我们创建一个小的矢量进行编码;在编码时，CKKSEncoder将隐式地用0填充到全尺寸(poly_modulus_degree / 2)。

   vector<double> input{ 0.0, 1.1, 2.2, 3.3 };
    cout << "Input vector: " << endl;
    print_vector(input);

现在我们用CKKSEncoder来编码。“输入”的浮点系数将由参数“scale”放大。这是必要的，因为即使在CKKS方案中，明文元素基本上也是多项式的整数系数。将比例尺scale 看作是确定编码的位精度是有意义的;这自然会影响结果的准确性。

在CKKS中，消息存储为模coeff_modulo(在BFV中，消息存储为模plain_modulo)，因此缩放后的消息不能太接近coeff_modulo。在这种情况下，我们的coeff_modules相当大(218位)，所以在这方面我们没什么可担心的。对于这个简单的示例，30位的范围就足够了。

    Plaintext plain;
    double scale = pow(2.0, 30);
    print_line(__LINE__);
    cout << "Encode input vector." << endl;
    //这里的编码需要scale，将输入向量编码为plain
    encoder.encode(input, scale, plain);

    /*
    We can instantly decode to check the correctness of encoding.
    */
    vector<double> output;
    cout << "    + Decode input vector ...... Correct." << endl;
    encoder.decode(plain, output);
    print_vector(output);

    /*
    The vector is encrypted the same was as in BFV.
    */
    Ciphertext encrypted;
    print_line(__LINE__);
    cout << "Encrypt input vector, square, and relinearize." << endl;
    encryptor.encrypt(plain, encrypted);

对密文的基本操作仍然很容易。在这里，我们对密文进行平方、解密、解码并打印结果。我们还注意到ecoding返回一个全尺寸的向量(poly_modulus_degree / 2);这是因为上面提到的隐式补零。

    evaluator.square_inplace(encrypted);
    evaluator.relinearize_inplace(encrypted, relin_keys);

    /*
    We notice that the scale in the result has increased. In fact, it is now the
    square of the original scale: 2^60.
    */
    cout << "    + Scale in squared input: " << encrypted.scale()
        << " (" << log2(encrypted.scale()) << " bits)" << endl;

    print_line(__LINE__);
    cout << "Decrypt and decode 先解密在解码." << endl;
    decryptor.decrypt(encrypted, plain);
    encoder.decode(plain, output);
    cout << "    + Result vector ...... Correct." << endl;
    print_vector(output);

CKKS方案允许在加密计算之间减少scale。这是使CKKS非常强大和灵活的基本和关键特性。我们将在3_levels 以及后面的 4_ckks_basic .cpp中详细讨论

void example_encoders()
{
    print_example_banner("Example: Encoders");

    /*
    Run all encoder examples.
    */
    example_integer_encoder();
    example_batch_encoder();
    example_ckks_encoder();
}

运行结果：