（前缀和、差分）总结（经典4大例题附图讲解）

1.一维前缀和：

典型模板题：前缀和
题目：输入一个长度为n的整数序列。接下来再输入m个询问，每个询问输入一对l, r。对于每个询问，输出原序列中从第l个数到第r个数的和。

输入格式
第一行包含两个整数n和m。
第二行包含n个整数，表示整数数列。
接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。

输出格式
共m行，每行输出一个询问的结果。

数据范围
1≤l≤r≤n1≤l≤r≤n,
1≤n,m≤1000001≤n,m≤100000,
−1000≤数列中元素的值≤1000−1000≤数列中元素的值≤1000

输入样例：
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例：
3
6
10

一维前缀和的作用：
快速求出原数组中一段数的和（原数组用来存储已确定的整数序列）。

题解：
运用递归的思想，根据 “s[i] = s[i-1] + a[i]” 求出前 i 个数的和，因此在求某一区间的和时，可以直接用“s[r] - s[l-1]” ，使得算法复杂度变为O(1)。【注意：这里原数组的下标是从1开始的，令 s[0]=0 有利于统一处理边界问题(少一个 if 特判）】。

//附AC代码
#include 
using namespace std;
const int N = 100010;

int n,m,a[N],s[N];

int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	
	for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
	
	while(m--)
	{
		int l,r;
		scanf("%d%d",&l,&r);
		printf("%d\n",s[r]-s[l-1]);
	}
	
	return 0;
}

OK，下面我们来讲二维的

2.二维前缀和：

典型模板题目：子矩阵的和
题目：
输入一个n行m列的整数矩阵，再输入q个询问。
每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数n，m，q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

输出格式
共q行，每行输出一个询问的结果。

数据范围
1≤n,m≤10001≤n,m≤1000,
1≤q≤2000001≤q≤200000,
1≤x1≤x2≤n1≤x1≤x2≤n,
1≤y1≤y2≤m1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000−1000≤矩阵内元素的值≤1000

输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17
27
21

二维前缀和的作用： 快速求出子矩阵中所有数的和（用一个二维数组存储原矩阵）。

题解：要想求得子矩阵中所有数的和，我们必须做到以下 2 点；
1.首先 初始化二维前缀和数组，也就是知道 s[i][j] 中所有数的和怎么算【通俗点来说，这个 s[i][j] 表示以 i 为长，j 为宽的小矩形，但是这个小矩形是以（1,1）为左上角，以（i，j）为右下角的】 。

2.其次，我们还要知道如何用 s[i][j]中所有数的和 来表示 以（x1,y1）为左上角 ，以 (x2,y2) 为右下角的子矩阵中所有数的和 。

【下面小白为了简约，就直言 s[i][j] 、（…）子矩阵了】。

下面，小白先说一下 求 s[i][j] 的 “背景知识” 。
根据二维矩阵（数组）的特征，我们是一行计算完，在累加下一行某一列中的数的（假定有一个数组 a[3][2]，它就表示一个第 3 行、第 2 列的数，我们知道，计算机在进行 “扫描” 时，是先把第一行扫描完，再对下一行进行扫描的，所以这个 a[3][2] 可以表示从第 1 行、第 1 列这个数，也就是 a[1][1] 按照小白之前所说的顺序一直 “扫描” 到了 a[3][2] ，这就是之后我们在求 s[i][j] 时的 “背景知识” ）。
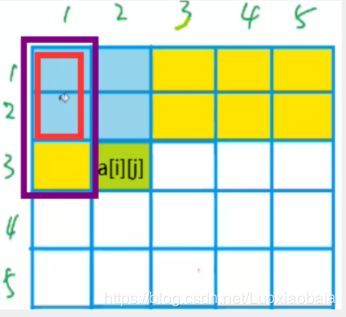
我们选取 n=5，m=5 的矩阵 首先，小白我来讲一下这个 s[i][j] 怎么算（ s[i][j] 对应 1个 i*j 的矩形，这个矩形即我们所要去表示的）【我们以 i=3，j=2 为例】。

1. 所有着色（喷涂颜色） 的部分表示 s[i][j] （以 i=3，j=2 为例）。
2. s[i-1][j] 表示 浅蓝色 的部分：s[2][2] 。
3. s[i][j-1] 表示 紫色方框 的部分：s[3][1]。
4. s[i-1][j-1] 表示 红色方框 的部分：s[2][1]，这个部分在 2 和 3 中分别 +1 次，要 -1 次，避免重复多算。
5. a[i][j] 表示 最后未算的一个小方块 ：a[3][2] ，我们要把它加上。
6. 最后，根据公式 “s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]” ，我们就可以求得所有的 s[i][j] 了。这个步骤也叫作 “初始化（二维）前缀和数组” 。

	// 初始化前缀和数组 
	for(int i=1;i<=n;i++)
	  for(int j=1;j<=m;j++) 
		 s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];

前面，我们已经解决了 s[i][j] 如何和计算的问题，下面我们就可以 表示这个 “ 以（x1,y1）为左上角 ，以 (x2,y2) 为右下角的子矩阵 ” 了。

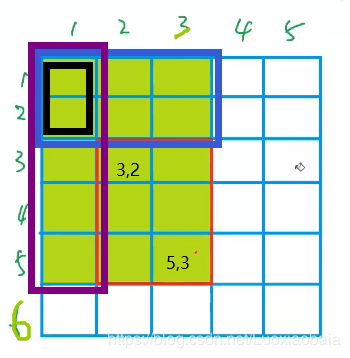
7. 黄绿色背景 矩形区域表示 s[x2][y2]： 即 s[5][3]
8. 粗体蓝色矩形 区域表示 s[x1-1][y2]： 即 s[2][3]
9. 粗体紫色矩形 区域表示 s[x2][y1-1]： 即 s[5][1]
10. 粗体黑色矩形 区域表示 s[x1-1][y1-1]： 即 s[2][1]，在2和3中共减了2次，多减1次，要+1次
11. 这个我们最终要求的红色矩形即表示为 “s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]” ，即：
    “s[5][3]-s[5][1]-s[2][3]+s[2][1]” 。

求 1 次这个红色子矩形即表示题目中的 1 次询问。

// 询问 
while(q--)
{
	int x1,y1,x2,y2;
	scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
	printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
}

好的，下面小白为大家附上这题的完整AC代码

#include 
using namespace std;
const int N = 1010;

int n,m,q;
int a[N][N],s[N][N];

int main()
{
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=n;i++) 
	  for(int j=1;j<=m;j++) 
		scanf("%d",&a[i][j]);
	
	// 初始化前缀和数组 
	for(int i=1;i<=n;i++)
	  for(int j=1;j<=m;j++) 
		 s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
	
	// 询问 
	while(q--)
	{
		int x1,y1,x2,y2;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
	}
	
	return 0;
}

“前缀和” 就讲到这里了，下面我们来讲对应的 “差分”，“差分”其实就是对前缀和的一个逆运用。

3.一维差分：

典型模板题：差分
题目：
输入一个长度为n的整数序列。
接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。
请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数n和m。第二行包含n个整数，表示整数序列。
接下来m行，每行包含三个整数l，r，c，表示一个操作。

输出格式
共一行，包含n个整数，表示最终序列。

数据范围
1≤n,m≤1000001≤n,m≤100000,
1≤l≤r≤n1≤l≤r≤n,
−1000≤c≤1000−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000−1000≤整数序列中元素的值≤1000

输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例：
3 4 5 3 4 2

我们先对 “差分” 做一个介绍：

思想： 构造 一个 b数组 ，使得原本的 a数组 是 b数组 的前缀和
作用： 如果要求原数组 的话, 对 b数组 求一遍 前缀和 就 OK，实现B->A 应用： 若对原 数组a 在区间 [l,r] 里每一个数都+c, 原本的复杂度是 O(n)，用 差分变成 O(1) 。 即：让b[l]+c,b[r+1]-c 。 这种情况下若要求原来的 a数组，只要扫描一遍 b数组,求其前缀和即可。
效果： 用差分,优化 “使a数组在某个区间的值全+c ” 这一算法，【时间复杂度: O(n)->O(1)】。

虽然小白在 思想 中提到 “构造”一词 ，但其实 “差分” 并不需要刻意去构造，只需要考虑如何去更新就行了。我们假设原数组a 中各个元素为 0，要求输入的 a数组 元素的值就相当于：“在假定区间的 a[i,i]（初始为0）上分别加上对应的输入数组元素的 a[i] 的值，这里用了一个insert插入函数” 。

下面，附上AC代码：

#include
using namespace std;
const int N = 100010;

int n,m;
int a[N],b[N];

void insert(int l,int r,int c)
{
	b[l] += c;
	b[r+1] -= c;
}

int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	
	for(int i=1;i<=n;i++) insert(i,i,a[i]);
	
	while(m--)
	{
		int l,r,c;
		scanf("%d%d%d",&l,&r,&c);
		insert(l,r,c);
	}
	
	for(int i=1;i<=n;i++) b[i]+=b[i-1];
	
	for(int i=1;i<=n;i++) printf("%d ",b[i]);
	
	return 0;
}

4.二维差分

典型例题：差分矩阵
题目：
输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c。
其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上c。请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数n,m,q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤10001≤n,m≤1000,
1≤q≤1000001≤q≤100000,
1≤x1≤x2≤n1≤x1≤x2≤n,
1≤y1≤y2≤m1≤y1≤y2≤m,
−1000≤c≤1000−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000−1000≤矩阵内元素的值≤1000

输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2

题解： 假设原矩阵为 a[i][j]，构造的差分矩阵为 b[i][j] ，满足 “原矩阵是差分矩阵的前缀和” ，即：使得a[i][j] 存的是其左上角所有的 b[i][j] 的和 。假设 a[i][j] 初始为 0，则 b[i][j] 初始为0，遍历 a[i][j] 中对应的所有的值，用 insert函数 插入一遍，即可完成所谓的 “差分矩阵的构造” 。这时题目便转化为 对b数组求二维前缀和 了。

附AC代码：

#include 
using namespace std;

const int N = 1010;

int n,m,q;
int a[N][N],b[N][N];

void insert(int x1,int y1,int x2,int y2,int c)
{
	b[x1][y1] += c;
	b[x2+1][y1] -= c;
	b[x1][y2+1] -= c;
	b[x2+1][y2+1] += c;
}

int main()
{
	scanf("%d%d%d",&n,&m,&q);
	
	for(int i=1;i<=n;i++)
	    for(int j=1;j<=m;j++)
	        scanf("%d",&a[i][j]);
	        
	for(int i=1;i<=n;i++)
	    for(int j=1;j<=m;j++)
	        insert(i,j,i,j,a[i][j]);
	
	while(q--)
	{
		int x1,y1,x2,y2,c;
		cin>>x1>>y1>>x2>>y2>>c;
		insert(x1,y1,x2,y2,c);
	}
	
	for(int i=1;i<=n;i++)
	    for(int j=1;j<=m;j++)
	        b[i][j] += b[i-1][j]+b[i][j-1]-b[i-1][j-1];
	        
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++) printf("%d ",b[i][j]);
		puts("");
	}
	return 0;
}

收尾 ！ OVER ！

其实这篇博客一度让我有些写不下去（最近确实比较累，还有些失眠…大一下学期的课程也在不断地更进中），但是想着 “贵在坚持” ，就又硬着头皮，继续码字了。总之，能够共同促进，毕竟是一件有价值、有意义的好事，希望大家多多支持哈。