房屋售价初体验

第二次学习继续采用Kaggle上面的一个经典竞赛——房屋售价预测。刚刚下载过数据文集后看到七十多种属性还是懵了一下，要比Titanic数据集稍显复杂，而且房价预测不是简单的dead or alive这样的二分类问题。所以第一次接触这样的预测模型我依然先参考一个较高的rank script，先对预测流程有所认识，再对模块进行学习。

和上一篇Titanic预测结构类似：数据集认识->缺失值处理->特征工程->base models->模型堆叠->训练预测

数据集认识

import pandas as pd
train = pd.read_csv('D:\\Dataset\\HousePrices\\train.csv')
test = pd.read_csv('D:\\Dataset\\HousePrices\\test.csv')

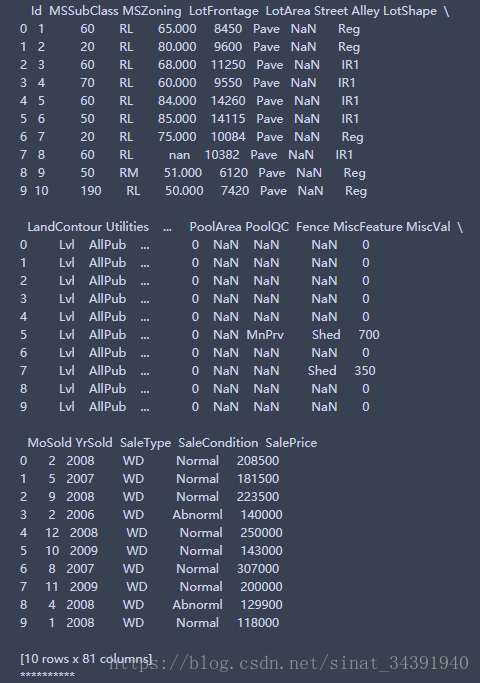
print(train.head(10))
print('*'*10)
train.info()

可以看出数据集中的属性类型和缺失值数量等信息。接下来进行缺失值处理。

编号Id不影响最终的房价可以先保存到变量中，代码如下：

train_Id = train['Id']
test_Id = test['Id']
train.drop("Id", axis = 1, inplace = True)
test.drop("Id", axis = 1, inplace = True)

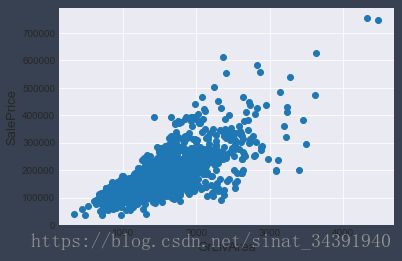
常识认为房屋面积越大价钱就应该越高，下面作图看一下房屋面积和最终价格的关系图：

import matplotlib.pyplot as plt
import seaborn as sns
color = sns.color_palette()
sns.set_style('darkgrid')

fig, ax = plt.subplots()
ax.scatter(x = train['GrLivArea'], y = train['SalePrice'])
plt.ylabel('SalePrice', fontsize=13)
plt.xlabel('GrLivArea', fontsize=13)
plt.show()

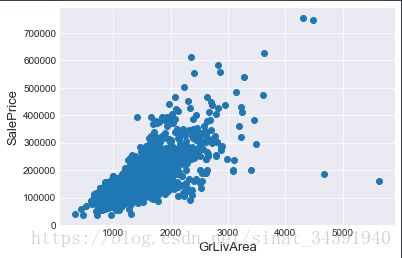
如图所示绝大多数的数据点都符合我们的常识，但还是发现有极少数的数据点房屋面积异常大但是房屋价格却异常低，所以在处理缺失值之前需要先清除数据中的异常值，代码如下:

train = train.drop(train[(train['GrLivArea']>4000) & (train['SalePrice']<300000)].index)
fig, ax = plt.subplots()
ax.scatter(train['GrLivArea'], train['SalePrice'])
plt.ylabel('SalePrice', fontsize=13)
plt.xlabel('GrLivArea', fontsize=13)
plt.show()

在这里还有一个小细节：为了能够更好的训练出线性模型，最好能够让目标值服从正态分布，从而减少偏态情况对模型训练的影响，因此这里还有一步关键步骤即正态分布转化，转化之前的房屋价格分布如下所示：

from scipy import stats
from scipy.stats import norm, skew

sns.distplot(train['SalePrice'] , fit=norm);
#正态拟合
(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))

plt.legend(['Normal dist. ($\mu=$ {:.2f} and $ \sigma=${:.2f})'.format(mu, sigma)], loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')

fig = plt.figure()
res = stats.probplot(train['SalePrice'], plot=plt)
plt.show()

这里用到的转换方法是Numpy中的log1p()方法，作用是进行log(1+x)转换，能够减少数据的偏态分布，代码如下：

#log1p()转换
train["SalePrice"] = np.log1p(train["SalePrice"])
#目标值分布显示
sns.distplot(train['SalePrice'] , fit=norm);
(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))

plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')

fig = plt.figure()
res = stats.probplot(train['SalePrice'], plot=plt)
plt.show()

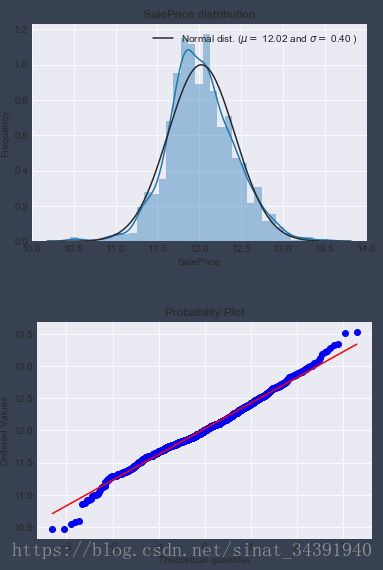
从sigma值的变化中可以明显看出数据偏态的特征已经几乎不存在了，可以放心进行缺失值的处理了。

缺失值处理
同时进行训练集和测试集的处理，先对数据集进行合并，代码如下：

#记录下训练集和测试集的大小
ntrain = train.shape[0]
ntest = test.shape[0]
y_train = train.SalePrice.values
all_data = pd.concat((train, test)).reset_index(drop=True)
all_data.drop(['SalePrice'], axis=1, inplace=True)
print("all_data size is : {}".format(all_data.shape))

all_data size is : (2917, 80)

接下来查看缺失值的比率，并将缺失值较多的前二十个属性输出：

all_data_na = (all_data.isnull().sum() / len(all_data)) * 100
all_data_na = all_data_na.drop(all_data_na[all_data_na == 0].index).sort_values(ascending=False)[:30]
missing_data = pd.DataFrame({'Missing Ratio' :all_data_na})
missing_data.head(20)

接下来按照以上缺失比例的大小顺序进行缺失值填充：

#数据描述中NA即没有，直接填充为“None”
all_data["PoolQC"] = all_data["PoolQC"].fillna("None")
all_data["MiscFeature"] = all_data["MiscFeature"].fillna("None")
all_data["Alley"] = all_data["Alley"].fillna("None")
all_data["Fence"] = all_data["Fence"].fillna("None")
all_data["FireplaceQu"] = all_data["FireplaceQu"].fillna("None")
#由于邻里之间到街边的距离都很类似，这里的缺失值可以取同一街区的平均值进行填充
all_data["LotFrontage"] = all_data.groupby("Neighborhood")["LotFrontage"].transform(lambda x: x.fillna(x.median()))
#以下的缺失值填充比较粗暴，可以尝试以下用Titanic里面的随机森林方法进行拟合填充，可能对模型准确度会有帮助。
for col in ('GarageType', 'GarageFinish', 'GarageQual', 'GarageCond'):
    all_data[col] = all_data[col].fillna('None')
for col in ('GarageYrBlt', 'GarageArea', 'GarageCars'):
    all_data[col] = all_data[col].fillna(0)
for col in ('BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF','TotalBsmtSF', 'BsmtFullBath', 'BsmtHalfBath'):
    all_data[col] = all_data[col].fillna(0)
for col in ('BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2'):
    all_data[col] = all_data[col].fillna('None')
all_data["MasVnrType"] = all_data["MasVnrType"].fillna("None")
all_data["MasVnrArea"] = all_data["MasVnrArea"].fillna(0)
all_data['MSZoning'] = all_data['MSZoning'].fillna(all_data['MSZoning'].mode()[0])
all_data = all_data.drop(['Utilities'], axis=1)
all_data["Functional"] = all_data["Functional"].fillna("Typ")
all_data['Electrical'] = all_data['Electrical'].fillna(all_data['Electrical'].mode()[0])
all_data['KitchenQual'] = all_data['KitchenQual'].fillna(all_data['KitchenQual'].mode()[0])
all_data['Exterior1st'] = all_data['Exterior1st'].fillna(all_data['Exterior1st'].mode()[0])
all_data['Exterior2nd'] = all_data['Exterior2nd'].fillna(all_data['Exterior2nd'].mode()[0])
all_data['SaleType'] = all_data['SaleType'].fillna(all_data['SaleType'].mode()[0])
all_data['MSSubClass'] = all_data['MSSubClass'].fillna("None")

#再查看缺失值
all_data_na = (all_data.isnull().sum() / len(all_data)) * 100
all_data_na = all_data_na.drop(all_data_na[all_data_na == 0].index).sort_values(ascending=False)
missing_data = pd.DataFrame({'Missing Ratio' :all_data_na})
missing_data.head()

特征工程
先将一些数据属性为int型的属性转换为类别型属性

all_data['MSSubClass'] = all_data['MSSubClass'].apply(str)
all_data['OverallCond'] = all_data['OverallCond'].astype(str)
all_data['YrSold'] = all_data['YrSold'].astype(str)
all_data['MoSold'] = all_data['MoSold'].astype(str)

所有的类别属性进行编码，代码如下：

from sklearn.preprocessing import LabelEncoder
cols = ('FireplaceQu', 'BsmtQual', 'BsmtCond', 'GarageQual', 'GarageCond', 
        'ExterQual', 'ExterCond','HeatingQC', 'PoolQC', 'KitchenQual', 'BsmtFinType1', 
        'BsmtFinType2', 'Functional', 'Fence', 'BsmtExposure', 'GarageFinish', 'LandSlope',
        'LotShape', 'PavedDrive', 'Street', 'Alley', 'CentralAir', 'MSSubClass', 'OverallCond', 
        'YrSold', 'MoSold')

for c in cols:
    lbl = LabelEncoder() 
    lbl.fit(list(all_data[c].values)) 
    all_data[c] = lbl.transform(list(all_data[c].values))

由于和面积相关的属性对房价预测比较重要，因此可以考虑增加新的属性用于建模：

all_data['TotalSF'] = all_data['TotalBsmtSF'] + all_data['1stFlrSF'] + all_data['2ndFlrSF']

接下来获取非对象属性的索引，进行数值化特征的偏态程度计算，并将偏差程度最大的十项属性输出：

numeric_feats = all_data.dtypes[all_data.dtypes != "object"].index
skewed_feats = all_data[numeric_feats].apply(lambda x: skew(x.dropna())).sort_values(ascending=False)
print("\nSkew in numerical features: \n")
skewness = pd.DataFrame({'Skew' :skewed_feats})
skewness.head(10)

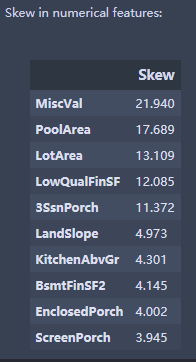
对于高度偏态分布的特征，用上面提到的log1p()方法进行转换就不能达到较高的满意度了。这里用到了一个新房常见的数据转换方法Box-Cox转换，功能和log1p()类似，都是能将偏态分布很大程度上转换成正态分布，以便于下一步的线性模型建立。
这里对偏离程度大于0.75的属性都进行Box-Cox变换，代码如下：

skewness = skewness[abs(skewness) > 0.75]
print("There are {} skewed numerical features to Box Cox transform".format(skewness.shape[0]))

from scipy.special import boxcox1p
skewed_features = skewness.index
lam = 0.15
for feat in skewed_features:
    all_data[feat] = boxcox1p(all_data[feat], lam)

There are 60 skewed numerical features to Box Cox transform

base models
接下来就可以进行base model训练了。

#先导入模型所需要的包
from sklearn.linear_model import ElasticNet, Lasso,  BayesianRidge, LassoLarsIC
from sklearn.ensemble import RandomForestRegressor,  GradientBoostingRegressor
from sklearn.kernel_ridge import KernelRidge
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import RobustScaler
from sklearn.base import BaseEstimator, TransformerMixin, RegressorMixin, clone
from sklearn.model_selection import KFold, cross_val_score, train_test_split
from sklearn.metrics import mean_squared_error
import xgboost as xgb
import lightgbm as lgb

现在可以将特征属性因子化，然后进行训练测试集的划分，代码如下：

all_data = pd.get_dummies(all_data)
train = all_data[:ntrain]
test = all_data[ntrain:]

仍然采用交叉验证，定义一个公用方法，用于返回模型训练得分代码如下：

n_folds = 5

def rmsle_cv(model):
    kf = KFold(n_folds, shuffle=True, random_state=42).get_n_splits(train.values)
    rmse= np.sqrt(-cross_val_score(model, train.values, y_train, scoring="neg_mean_squared_error", cv = kf))
    return(rmse)

接下来开始定义模型的参数，代码如下：

lasso = make_pipeline(RobustScaler(), Lasso(alpha =0.0005, random_state=1))

ENet = make_pipeline(RobustScaler(), ElasticNet(alpha=0.0005, l1_ratio=.9, random_state=3))

KRR = KernelRidge(alpha=0.6, kernel='polynomial', degree=2, coef0=2.5)

GBoost = GradientBoostingRegressor(n_estimators=3000, learning_rate=0.05,
                                   max_depth=4, max_features='sqrt',
                                   min_samples_leaf=15, min_samples_split=10, 
                                   loss='huber', random_state =5)

model_xgb = xgb.XGBRegressor(colsample_bytree=0.4603, gamma=0.0468, 
                             learning_rate=0.05, max_depth=3, 
                             min_child_weight=1.7817, n_estimators=2200,
                             reg_alpha=0.4640, reg_lambda=0.8571,
                             subsample=0.5213, silent=1,
                             random_state =7, nthread = -1)

model_lgb = lgb.LGBMRegressor(objective='regression',num_leaves=5,
                              learning_rate=0.05, n_estimators=720,
                              max_bin = 55, bagging_fraction = 0.8,
                              bagging_freq = 5, feature_fraction = 0.2319,
                              feature_fraction_seed=9, bagging_seed=9,
                              min_data_in_leaf =6, min_sum_hessian_in_leaf = 11)

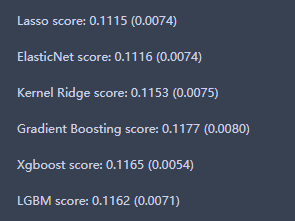
进行模型的训练并打印得分，代码如下：

score = rmsle_cv(lasso)
print("\nLasso score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(ENet)
print("ElasticNet score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(KRR)
print("Kernel Ridge score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(GBoost)
print("Gradient Boosting score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(model_xgb)
print("Xgboost score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(model_lgb)
print("LGBM score: {:.4f} ({:.4f})\n" .format(score.mean(), score.std()))

模型训练结束后就可以开始进行集成训练了。这里利用面向对象的编程思想，定义了模型的训练和预测方法。

class AveragingModels(BaseEstimator, RegressorMixin, TransformerMixin):
    def __init__(self, models):
        self.models = models
        
    def fit(self, X, y):
        self.models_ = [clone(x) for x in self.models]
        for model in self.models_:
            model.fit(X, y)
        return self

    def predict(self, X):
        predictions = np.column_stack([model.predict(X) for model in self.models_])
        return np.mean(predictions, axis=1)

对模型的得分进行平均，得出新的模型的均值和方差，代码如下：

averaged_models = AveragingModels(models = (ENet, GBoost, KRR, lasso))
score = rmsle_cv(averaged_models)
print(" Averaged base models score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))

Averaged base models score: 0.1091 (0.0075)

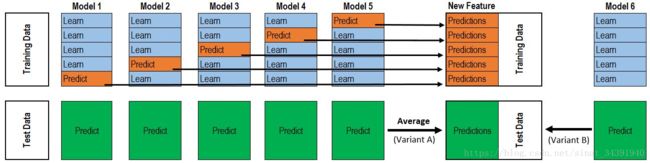
除了简单的求模型平均分的方法，还有一种不简单的堆叠方式，即添加元模型层。
在k份数据子集k次迭代训练的过程中，每次都会把其余的k-1份数据预测结果作为下一轮元模型的训练输入，因此k-fold训练之后，元模型的训练集也就准备好了，再对元模型的数据集进行训练即可，如下图所示：

和上面一样，定义一个类用于定义模型的训练和预测方法，代码如下：

class StackingAveragedModels(BaseEstimator, RegressorMixin, TransformerMixin):
    def __init__(self, base_models, meta_model, n_folds=5):
        self.base_models = base_models
        self.meta_model = meta_model
        self.n_folds = n_folds
        
    def fit(self, X, y):
        self.base_models_ = [list() for x in self.base_models]
        self.meta_model_ = clone(self.meta_model)
        kfold = KFold(n_splits=self.n_folds, shuffle=True, random_state=156)
        
        out_of_fold_predictions = np.zeros((X.shape[0], len(self.base_models)))
        for i, model in enumerate(self.base_models):
            for train_index, holdout_index in kfold.split(X, y):
                instance = clone(model)
                self.base_models_[i].append(instance)
                instance.fit(X[train_index], y[train_index])
                y_pred = instance.predict(X[holdout_index])
                out_of_fold_predictions[holdout_index, i] = y_pred

        self.meta_model_.fit(out_of_fold_predictions, y)
        return self

    def predict(self, X):
        meta_features = np.column_stack([
            np.column_stack([model.predict(X) for model in base_models]).mean(axis=1)
            for base_models in self.base_models_ ])
        return self.meta_model_.predict(meta_features)

接下来进行模型训练，并且打印出模型的均值和方差：

stacked_averaged_models = StackingAveragedModels(base_models = (ENet, GBoost, KRR),
                                                 meta_model = lasso)

score = rmsle_cv(stacked_averaged_models)
print("Stacking Averaged models score: {:.4f} ({:.4f})".format(score.mean(), score.std()))

Stacking Averaged models score: 0.1085 (0.0074)

可见误差值又有所下降。接下来将模型进行集成融合，打印出每个模型的误差值：

def rmsle(y, y_pred):
    return np.sqrt(mean_squared_error(y, y_pred))
#StackedRegressor
stacked_averaged_models.fit(train.values, y_train)
stacked_train_pred = stacked_averaged_models.predict(train.values)
stacked_pred = np.expm1(stacked_averaged_models.predict(test.values))
print(rmsle(y_train, stacked_train_pred))
#XGBoost
model_xgb.fit(train, y_train)
xgb_train_pred = model_xgb.predict(train)
xgb_pred = np.expm1(model_xgb.predict(test))
print(rmsle(y_train, xgb_train_pred))
#LightGBM
model_lgb.fit(train, y_train)
lgb_train_pred = model_lgb.predict(train)
lgb_pred = np.expm1(model_lgb.predict(test.values))
print(rmsle(y_train, lgb_train_pred))

0.0781571937916
0..0785165142425
0.0716757468834

给不同的模型赋予不同的权值，得到最终的误差值：

print('RMSLE score on train data:')
print(rmsle(y_train,stacked_train_pred*0.70 + xgb_train_pred*0.15 + lgb_train_pred*0.15 ))

RMSLE score on train data:
0.07586557397142984

进行最终的预测和提交数据生成：

test = pd.read_csv('D:\\Dataset\\HousePrices\\test.csv')

ensemble = stacked_pred*0.70 + xgb_pred*0.15 + lgb_pred*0.15
sub = pd.DataFrame()
sub['Id'] = test['Id']
sub['SalePrice'] = ensemble
sub.to_csv('D:\\Dataset\\HousePrices\\submission.csv',index=False)

总结
这次实验学到了数据转换的两个方法log1p()和Box-Cox方法，但是对其原理没有过多了解。关于缺失值模拟那一步，还可以参考Titanic中的随机森林模拟年龄。特征工程中只加了一个面积属性，下一篇文章我会把我的idea实现。