MLlib回归算法（线性回归、决策树）实战演练--Spark学习（机器学习）

最近太忙，自己的机器学习进度耽误了两个星期，现在才把回归这一章看完。闲话不多说，本篇文章依旧是《Spark机器学习》中的内容。书上的代码全部是用python写的，但是由于我最近一直使用的是Scala，所以本篇博客使用的是scala，当然这样就没法像书中那样画图了。
第六章将的是回归算法，主要用到的是线性回归与决策树算法，老规矩这里不讲原理（主要是自己讲不清楚），想知道原理的建议参考Andrew NG机器学习课程或查看其他资料。另外关于API查看官方文档（个人感觉官方文档很有用）。
Andrew NG机器学习：https://www.coursera.org/learn/machine-learning
官方文档：http://spark.apache.org/
下面进入正题

数据源

本次回归算法用到的数据源为自行车租车数据，下载地址为：http://archive.ics.uci.edu/ml/datasets/Bike+Sharing+Dataset，主要用hour.csv数据。
数据描述：此数据是根据一系列的特征预测每小时自行车租车次数。数据中字段分别为：
instant：记录ID
dteday：时间
season：四季信息
yr：年份（2011或2012）
mnth：月份
hr：当天时刻
holiday：是否节假日
weekday：周几
workingday：当天是否工作日
weathersit：表示天气类型的参数
temp：气温
atemp：体感温度
hum：湿度
windspeed：风速
cnt：目标变量，每小时的自行车租车量
一共15个字段，主要目的是预测最后一个字段的租车量。研究数据发现头两个字段对于预测结果没什么用处，所以这里不考虑。

一、线性回归

想必初学机器学习的同学都是从这个算法开始的吧，其实就是给一些特征然后预测一个值例如预测房价、股票等。
在spark的MLlib中回归算法与分类算法的用法其实相似，主要区别就是在LabeledPoint中的label不同，分类算法是具体的类别，而回归算法是一个不定的值。

1.特征提取

观察数据发现从第3到第10个字段是类型变量（类型变量就是取值一直就只有那么几种，例如星期几、天气状况等），11到14字段是实数变量（实数变量就是一个无法确定的值）这里的值已经进行过归一化处理了，如果没归一化处理需先归一处理，可以提高准确度。

类别特征

其实上一篇博客已经讲过类别型数据怎么提取特征，主要方法就是将类别数据转换为二元向量，就是用一个向量来表示类别。举个例子就是如果水果有三类分别为苹果、香蕉、梨。一般在类别数据中记录的形式为1：苹果，2：香蕉，3：梨。将其转换为二元向量之后就是001：苹果，010：香蕉，100：梨。如果不转换为二元特征算出来会有错误，本数据我试过如果不转换预测结果是负数。

实数特征

实数特征一般就不用处理可以直接使用了，但是如前面提到的一般要归一处理

2.代码实现

import breeze.linalg.sum
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.{LinearRegressionWithSGD, LabeledPoint}
import org.apache.spark.mllib.tree.DecisionTree
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkContext, SparkConf}

/**
  * Created by luo on 12/18/15.
  */
object ML_Regression {

  def main(args: Array[String]) {

    val conf=new SparkConf().setAppName("regression").setMaster("local[1]")
    val sc=new SparkContext(conf)

    val records=sc.textFile("/home/luo/sparkLearning/MLData/hour_noheader.csv").map(_.split(",")).cache()


    val mappings=for(i<-Range(2,10))yield get_mapping(records,i)

    val cat_len=sum(mappings.map(_.size))
    val num_len=records.first().slice(10,14).size
    val total_len=cat_len+num_len

    //linear regression data 此部分代码最重要，主要用于产生训练数据集，按照前文所述处理类别特征和实数特征。
    val data=records.map{record=>

      val cat_vec=Array.ofDim[Double](cat_len)
      var i=0
      var step=0
      for(filed<-record.slice(2,10))
        {

          val m=mappings(i)
          val idx=m(filed)
          cat_vec(idx.toInt+step)=1.0
          i=i+1
          step=step+m.size
        }

      val num_vec=record.slice(10,14).map(x=>x.toDouble)

      val features=cat_vec++num_vec
      val label=record(record.size-1).toInt


      LabeledPoint(label,Vectors.dense(features))
    }

    // val categoricalFeaturesInfo = Map[Int, Int]()
    //val linear_model=DecisionTree.trainRegressor(data,categoricalFeaturesInfo,"variance",5,32)
    val linear_model=LinearRegressionWithSGD.train(data,10,0.1)
    val true_vs_predicted=data.map(p=>(p.label,linear_model.predict(p.features)))
    //输出前五个真实值与预测值
    println( true_vs_predicted.take(5).toVector.toString())
  }

  def get_mapping(rdd:RDD[Array[String]], idx:Int)=
  {
  rdd.map(filed=>filed(idx)).distinct().zipWithIndex().collectAsMap()
  }

}

上诉代码运行之后结果为：

Vector((16.0,135.94648455498353), (40.0,134.38058174607252), (32.0,134.18407938613737), (13.0,133.88699144084512), (1.0,133.77899037657545))

每组数据第一个为真实值，第二个为预测结果顿时傻眼了，这相差也太大了吧。不过没事，关于机器学习写完了代码只是完成了一小步，更多的工作是花在参数调优。例如将LinearRegressionWithSGD.train(data,10,0.1)中的0.1改为0.5之后结果就为：

Vector((16.0,88.03570714076662), (40.0,84.43777528417648), (32.0,83.56296823759422), (13.0,84.26995929901776), (1.0,83.74573422163347))

由于本篇博客我想对决策树更深入的研究，所以对线性回归模型的性能调优我就不写了。

二、决策树

决策树一般可以用于处理非线性问题，本数据源其实就是属于非线性问题，理论上使用决策树的结果会更加准确，下面我们来是不是如我们所料。

1.特征提取

决策树的训练数据就不需要对将类别特征转为二元向量了，所以特征提取就非常简单。只需提取数据中第3到第10个字段的信息并转为Double类型就行了。特征提取以及训练数据产生代码如下：

val data=records.map{record=>
      val features=record.slice(2,14).map(_.toDouble)
      val label=record(record.size-1).toDouble
      LabeledPoint(label,Vectors.dense(features))
    }

2.代码实现

训练数据生成以后就可以训练模型了，具体完整代码如下，同样也输出预测的头五个值进行观察。

import breeze.linalg.sum
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.{LinearRegressionWithSGD, LabeledPoint}
import org.apache.spark.mllib.tree.DecisionTree
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkContext, SparkConf}

/**
  * Created by luo on 12/18/15.
  */
object ML_Regression {

  def main(args: Array[String]) {

    val conf=new SparkConf().setAppName("regression").setMaster("local[1]")
    val sc=new SparkContext(conf)

    val records=sc.textFile("/home/luo/sparkLearning/MLData/hour_noheader.csv").map(_.split(",")).cache()


    val mappings=for(i<-Range(2,10))yield get_mapping(records,i)

    val cat_len=sum(mappings.map(_.size))
    val num_len=records.first().slice(10,14).size
    val total_len=cat_len+num_len
      //decision tree data
    val data=records.map{record=>
      val features=record.slice(2,14).map(_.toDouble)
      val label=record(record.size-1).toDouble
      LabeledPoint(label,Vectors.dense(features))

    }

     val categoricalFeaturesInfo = Map[Int, Int]()
    val tree_model=DecisionTree.trainRegressor(data,categoricalFeaturesInfo,"variance",5,32)
//    val linear_model=LinearRegressionWithSGD.train(data,10,0.5)
    val true_vs_predicted=data.map(p=>(p.label,tree_model.predict(p.features)))
    println( true_vs_predicted.take(5).toVector.toString())

  }

  def get_mapping(rdd:RDD[Array[String]], idx:Int)=
  {
rdd.map(filed=>filed(idx)).distinct().zipWithIndex().collectAsMap()
  }

}

运行结果如下所示：

Vector((16.0,54.913223140495866), (40.0,54.913223140495866), (32.0,53.171052631578945), (13.0,14.284023668639053), (1.0,14.284023668639053))

模型中均采用的默认参数，结果相比线性回归效果明显。

三、性能评估

1.均方误差和均方根误差

(1) MSE是均方误差，是用作最小二乘回归的损失函数，表示所有样本预测值和实际值平方差的平均值。公式如下：

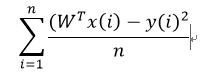
(2) RMSE是MSE的平方根

(3) 平均绝对误差（MAE）：预测值与实际值的绝对值差的平均值

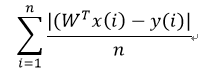
(4) 均方根对数误差（RMSLE）：预测值和目标值进行对数变换后的RMSE.
其中求MSE、MAE、RMSLE的scala代码如下：

  val MSE=true_vs_predicted.map(value=>
    {
      (value._1-value._2)*(value._1-value._2)
    }).mean()

    val MAE=true_vs_predicted.map(value=>
    {
      math.abs(value._1-value._2)
    }).mean()

    val RMSLE=true_vs_predicted.map(value=>
    {
      math.pow(math.log(value._1+1)-math.log(value._2+1),2)
    }).mean()

最后求得的结果为：

MSE:11560.797822393652
MAE:71.09690694470646
RMSLE:0.39174394027474707

四、训练集与测试集

之后我用到机器学习的数据都是训练集与测试集相同，但是在实际设计中肯定不会是这样的。一般做法是将数据分为三部分，分别为训练集、交叉验证集和测试集，这里我就图方便只将数据分为训练集与测试集两部分，比例分别为0.7,0.3。
在spark的rdd中提供了randomSplit的方法用户切分数据集，方法介绍如下：

def
randomSplit(weights: Array[Double], seed: Long = Utils.random.nextLong): Array[RDD[T]]
Randomly splits this RDD with the provided weights.
weights
weights for splits, will be normalized if they don't sum to 1
seed
random seed
returns
split RDDs in an array

因此在决策树树代码中将data切分为train_data和test_data。

val data=records.map{record=>
      val features=record.slice(2,14).map(_.toDouble)
      val label=record(record.size-1).toDouble
      LabeledPoint(label,Vectors.dense(features))

    }.randomSplit(Array(0.7,0.3),11L)

    val train_data=data(0)
    val test_data=data(1)

最后用train_data作为训练集，test_data作为测试集得到结果为：

MSE:12040.251369023337
MAE:73.43513348748438
RMSLE:0.40856625833634497

总结：本篇博客就写到这里，主要介绍的是回归算法的一些实例，大部分内容来自《Spark机器学习》学习之后的一些想法，欢迎大家一起交流学习。