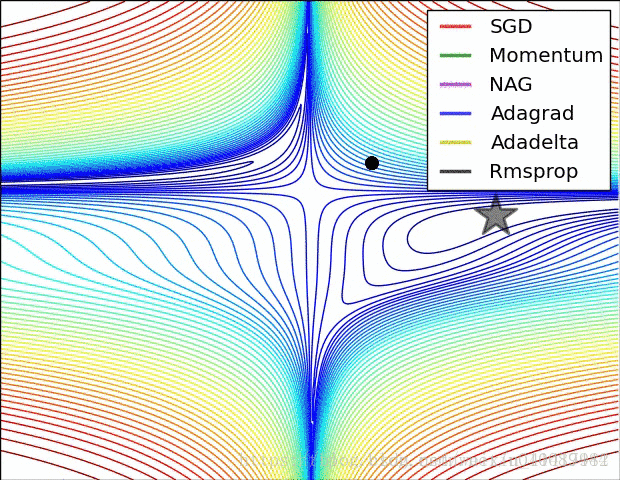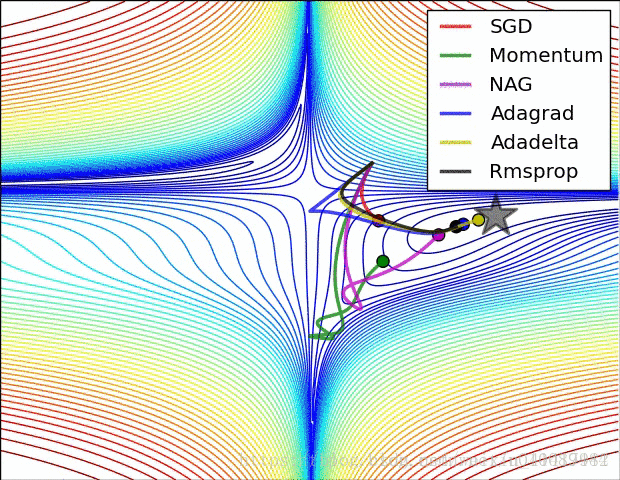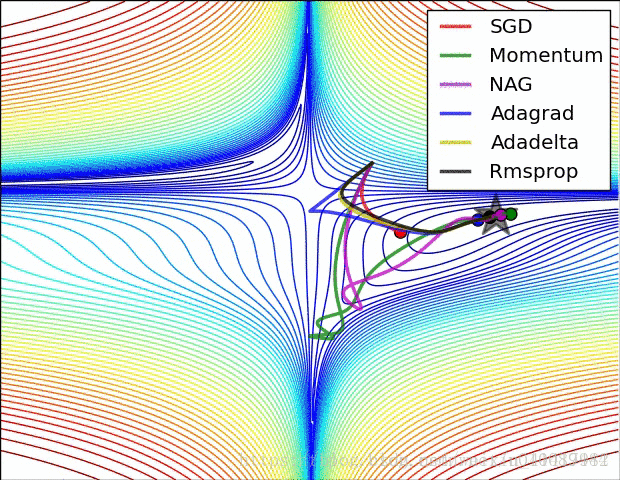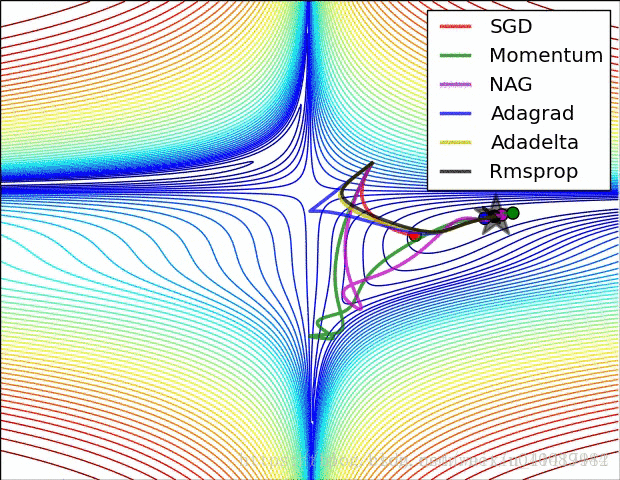
优化器（Optimizer）介绍

Gradient Descent（Batch Gradient Descent，BGD）

梯度下降法是最原始，也是最基础的算法。

它将所有的数据集都载入，计算它们所有的梯度，然后执行决策。（即沿着梯度相反的方向更新权重）

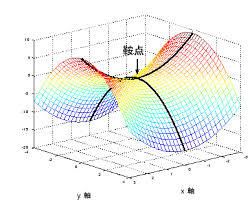
优点是在凸函数能收敛到最小值。但显而易见的是，这方法计算量太大。假如我们的数据集很大的话，普通的GPU是完全执行不来的。还有一点，它逃不出鞍点，也容易收敛到局部最小值（也就是极小值）。

Stochastic Gradient Descent

参考:
https://zhuanlan.zhihu.com/p/27609238 (关于海森矩阵的没学过）
https://blog.csdn.net/bvl10101111/article/details/72615621 (Momentum)

随机梯度下降法相比较BGD，其实就是计算梯度时根据的数据不同。SGD根据的是一整个数据集的随机一部分（上网有些介绍都是说根据每一个样本，emmm，但是现在都是采用一个随机的部分样本）。

也就是说，它更新的速度比较频繁。因为我们随机选取的小批量数据(mini-batch)并不是太多，所以计算的过程也并不是很复杂。相比起BGD，我们在相同的时间里更新的次数多很多，也自然能更快的收敛。

但还是有缺点的，一个是CS231n提到的：

这里我不是很明了，涉及到了海森矩阵。原话是假设二维的例子中损失函数在某个方向变化很快但在另外个方向变化很慢，SGD就会在变化慢的方向来回，导致变化快的方向不会有很大的跨度。

不过在看了一个例子我觉得很形象，在https://zhuanlan.zhihu.com/p/21486826。它用：

类比：

我们可以很清楚的联想起来，在滑板的时候，假如你的起点在两边的边上，你能够想象，你下降最快的方向不是沿着左右两边，而是斜着向下。这样，我们权重更新的方向也会跟着一样。

还有一个是噪声会相对较大。这个很容易理解，因为你应用在整个训练集的模型，它更新的梯度却是利用训练集的一部分。但在网上找资料的时候，https://zhuanlan.zhihu.com/p/36816689，讲了噪声如何帮助SGD逃出鞍点。

但是CS231n是用了另外一种方法来使得SGD克服上面所提到的缺点，例如。那就是加上一个动量（Momentum）。

可以看到，现在SGD更新的梯度不仅是算出来的梯度，更要加上上一步的梯度。但有个参数 ρ ρ 让我们调整上一步梯度占的比重。

现在来看看如何做到克服上面的问题的。前面说到无法逃离鞍点和极小值（哪个方向损失都增大）是因为梯度都为0，因此停滞不前。但由于这个Momentum的出现，导致在哪个地点都还有一定的梯度，所以我们的网络可以继续更新下去。至于那个之字形，我画了一个图。

在标记的蓝色那个点，如果不加Momentum，更新的方向就是蓝色向量。但是由于我们加了个上一步的梯度，也就是绿色的向量，现在我们更新的向量是黄色的，也就是不再是垂直方向，而是在水平方向。这在一定程度就克服了上面说的缺陷。

Nesterov

图片来自于：https://blog.csdn.net/tsyccnh/article/details/76673073（也有讲解不同的优化器）

Momentum:

Nesterov:

其实这个作图有点让人混乱，因为这样看它们好像是更新一样的梯度。其实不是的。在第二幅图里面，C走到D是根据C那个点的梯度，然后作者把BD连起来说这是B点实际梯度下降的方向。所以，我们应该要搞清楚！！！它们不是一样的。

我们可以让每个字母代表对应点的参数， g(a) g ( a ) 代表 a a 的梯度，那:

Momentum:g(b)g(b)′Nesterov:g(b)g(b)′=ρg(a)+g(b)=b−α⋅g(b)=ρg(a)+g(b−α⋅ρg(a))=ρg(a)+g(c)=b−α⋅g(b) M o m e n t u m : g ( b ) = ρ g ( a ) + g ( b ) g ( b ) ′ = b − α ⋅ g ( b ) N e s t e r o v : g ( b ) = ρ g ( a ) + g ( b − α ⋅ ρ g ( a ) ) = ρ g ( a ) + g ( c ) g ( b ) ′ = b − α ⋅ g ( b )

当然，也有人认为Nesterov只是多算了一次梯度，但事实并不是这样。
有位大神在http://www.360doc.com/content/16/1010/08/36492363_597225745.shtml最下面推理了过程，可以得出结论为：

结论：在原始形式中，Nesterov Accelerated Gradient（NAG）算法相对于Momentum的改进在于，以“向前看”看到的梯度而不是当前位置梯度去更新。经过变换之后的等效形式中，NAG算法相对于Momentum多了一个本次梯度相对上次梯度的变化量，这个变化量本质上是对目标函数二阶导的近似。由于利用了二阶导的信息，NAG算法才会比Momentum具有更快的收敛速度。

AdaGrad

我们累计每一次梯度的平方，接着让学习率除以它的开方。这个的作用是为了改变不同参数的学习率。假如一个参数的梯度一直很大，那么通过这个约束，它改变的就越少。假如一个参数的梯度一直很小，那么通过这个约束它，它变化的也就越快。这里的 1e−7 1 e − 7 是防止分母为0。

但问题是，因为是一直在累积的，这个grad_squared一定会变得越来越大，最后的结果是，权重更新的步长也会不可避免的变得很小。为了克服这个问题，有了RMSpro。

RMSprop

可以看出来，它只是改变了grad_squared。添加了一个衰减率（一般0.9或者0.99），可以使得grad_squared的变化不会因为时间的累积而变得太大。

但也由于衰减的问题，grad_squard是可能导致我们训练一直在变慢的。(我理解是后面累积的梯度太少了，但因为前面的梯度太多，没有办法加速，当然，我没有找到资料，但斯坦福课程上面Johnson是这样说的）

PS：有些人将RMSprop和Nesterov结合起来。

Adam

可以看出来，红色的部分是类似与Momentum的方法，而蓝色的部分则是利用了RMSprop的衰减。因此这个算法是很好的结合了这两个的优点。

之所以有绿色方框的Bias Correction是因为想要避免一个情况：一开始的梯度太小，因此学习率除以second_moment的值太大，步长太大容易跑到一个奇怪的地方。导致收敛之后的效果不好。因此我们有了Bias correction，学习率也是除以second_unbias。

Adam一般来说是收敛最快的优化器，所以被用的更为频繁。当然，它还有变体AdamMax，但知道了Adam再去看其它也不是很难了。

总览

图片来自： https://blog.csdn.net/u010089444/article/details/76725843
图片作者：Alec Radford