自然语言处理——向量语义及嵌入（余弦相似度、TF-IDF、Word2Vec）

向量语义及嵌入

向量语义

  在类似的环境中不同事物产生出相似的特征，这一现象称为分布假设。而在语言中，处于相同语境中的不同词语也会出现类似的意义，向量语义正是分布假设的实例化，即将文本的符号表示转换为语义空间中的向量表示。根据词语所处语境，通过无监督方式学习到该词语的语义表示。

词语义

  词语义主要包括以下几个方面：
  词的相似性：同义词并不多，不过多数词都有多个相似词。同义到相似的转换，实际上是词义关系到词语关系的转换。词语相似性有助解决问答、摘要等任务。

  词相关：在同一语境下的不同词语存在这一定的关联性，比如“用勺子吃饭”这句话中，勺子和米饭存在一定的关系，两者共同完成了吃饭这件事。处理词语的关系，可以帮助简化问题，避免发生歧义。

  语义框架和语义角色：框架语义表示在特定类型中，一个表示事件参与者与参与角度的词语集合。例：在商品交易中，事件过程可以提取为一个实体把钱给另外一个实体，由此获取商品或服务。事件的结果是商品流转、服务完成。通过词汇化编码为：买（顾客角度）、卖（商家角度）、付款（货币角度），名词：顾客。框架内有语义角色，比如顾客、商家、商品、货币等。通过语义框架可对句子进行变换，即：”张三从李四那里购买了一个电脑“ 可转化为 “李四将一个电脑卖给了张三” 。语义框架的构建可用于问答系统或者机器翻译。

  隐含意义：每个词语都具有其相对应的隐含意义，大多表现为情感。比如“神清气爽”具有积极向上的情感意义，“垂头丧气”具有低迷消极的意义，隐含意义主要用于情感分析、舆情监测等。

向量语义

  了解了词语义的基本内容后，怎样利用这些特性内容的？通过向量语义这一计算模型，可以很好的处理词语义的各个内容。

  向量语义起源于50年代语言学与哲学。维特根斯坦（1953）表示“词语的意义决定于它在语言中的使用”，与其为每个词提供定义，不如把词表示成说话人的实际使用方式。进一步得到，两个词如果具有类似的语境，就有类似的意义。

  向量语义结合了两种方向：
    1. 分布：通过观测语境中的其他词语来定义一个词。
    2. 向量：把一个词定义为一个由一串数字表示的向量，即N维空间中的一个点。

  词嵌入：表示词语的向量被称为词嵌入（将词语嵌入到特点的向量空间）。优势在于通过无监督的方式进行学习，找到词语相似性与短语相似性，从而进行分类。

图1：词和短语的二维投影   图一展示了一些词和短语的二维投影，可以看到具有相似意义的词在空间中相互靠近。   词向量常用的模型有：cosine(余弦相似度，使用向量计算两个单词、句子、短文的相似性)、TF-IDF模型（将词语变成稀疏向量）、Word2Vec（构造具有语义特性的密集短向量）。

词与向量

  通过共现矩阵的方式将词与向量联系起来，表现形式有Term-Document Matrix、Term-Context Matrix。
  Term-Document Matrix：以词在文章中的出现频次为基准，构成有V行（词汇表中的每一个词汇类型）D列（集合中的每一个文章）的矩阵，比较每篇文章在V*D维向量空间中所构成的向量。
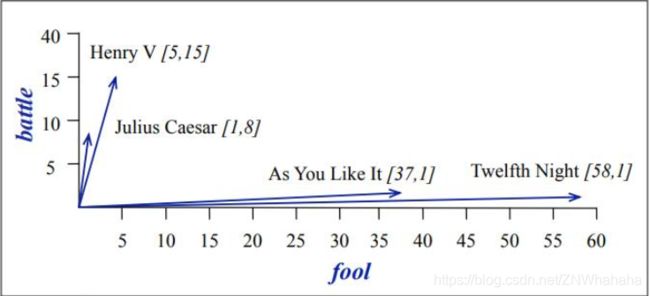
  以莎士比亚的四部戏剧为例，从中选择“battle”、“good”、”fool“、”wit“四个词，统计他们在四部戏剧中出现的次数，数据如图2所示：

图2：词文档矩阵   由图所示，文档"as you like it"的向量就是[1, 114, 36, 20]。比较某个维度上的数字可以确定文档的相似性。每一个文档就是向量空间里得一个点，即文章产生向量。  Term-Document Matrix最初用于文档信息检索。两篇类似的文档所用的词也接近，反之亦然。向量的匹配过程可以使用tf-idf和余弦相似矩阵。

  选取battle和fool两词作为两个维度时，4部戏剧所表现的向量如图3所示：

图3：文档向量的空间可视图   真正的Term-Document Matrix不会只有4行4列，这里只是为了举例方便。

  Term-Context Matrix：对于文档，相似的文档有相似的文档向量，这一原则同样适用于词，相似的词出现在相似的文档中，所以它们有相似的词向量。
  其维度由不同类型的上下文所决定。与词文档矩阵不同的地方在于，矩阵的列由单词而不是文档标记。由此该矩阵的维数是：V*V，每个单元格记录行（目标）词和列（上下文）词在训练集中的某些上下文同时出现的次数。当上下文是整个文档时，单元格表示两个词在同一文档中出现的次数。通常设置一个包含9个单词的窗口。以目标词为中心，窗口包含的词即为上下文。
  矩阵中单元格的数值通过统计每一次目标单词出现时，窗口内其他单词的出现个数填充。图4为从语料库中计算出4个词的词共现矩阵。图5为可视化。

图4：词-上下文矩阵

图5：词向量的可视化

余弦相似度

  余弦相似度的作用：为了定义两个目标词v和w之间的相似度，需要一个可度量的量来获取这两个词的向量同时返回向量的相似度。余弦相似度是目前最常用的度量相似度的方法，测量的是向量间夹角的余弦。
  在NLP中使用向量相似性的多数度量方法都是基于点积（或称内积），点积之所以可以作为相似度的测量指标，是因为如果两个向量在同一个维度都有较大的值，点积的结果就大。如果向量正交，则点积为0。点击可以表示出向量之间的强相异性。公式如下：$$dotproduct(v,w)=v\cdot w=\sum _{i=1}^N{v}_i{w}_i=v_1{w}_1+v_2{w}_2+...+v_N{w}_N$$
  然后使用点积会出现一个运算问题，就是词频率越高的词向量越长，而向量越长，点积越大。我们应当消除向量长度对向量点积的影响，方法是点积除以两个向量的长度之积，其实就是求向量夹角的余弦值，即：$$a\cdot b=|a||b|\cos \theta$$ $$\frac{a\cdot b}{|a||b|}=\cos \theta$$
  则两个向量v和w的余弦相似度的计算方式是：$$cosine(v,w)=\frac{v\cdot w}{|v||w|}=\frac{{\sum }_{i=1}^N{v}_i{w}_i}{\sqrt{{\sum }_{i=1}^N{v}_i^2}\sqrt{{\sum }_{i=1}^N{w}_i^2}}$$
  由于原始词频值不为负数，则上式的余弦值范围从0到1。
  注意：在某些情况下，可以通过将每个向量除以其长度进行标准化，从而创建长度为1的单位向量（即：$a÷|a|$）,对于单位向量，点积与余弦的结果相同。
  通过下表可以计算出"cherry"和"digital"哪个更接近"information"。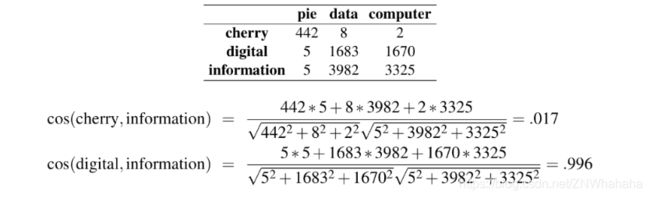
  由计算出的值可知，“digital"比"cherry"更接近"information”。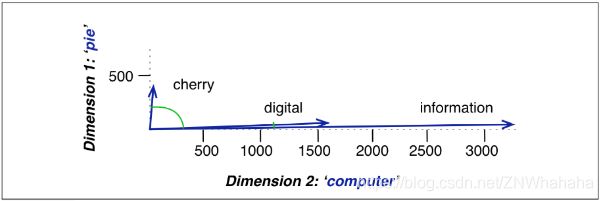

图5：余弦相似性的粗略演示图   如图5所示，当两个向量更相似时，余弦较大，但图像角度较小。

TF-IDF

  TF-IDF算法:一个词语在一篇文章中出现次数越多, 同时在所有文档中出现次数越少, 越能够代表该文章。主要解决文章中出现的无意义频繁词的问题。该算法遵循2个基准：

1. 词频（term frequency——TF）算法不直接统计文档里某词的数量，而是使用数量的对数（log10(词频)）进行再加工，因为某词出现100次，并不代表它与所在文档有100倍的相关性。$$t{f}_{t,d}=\{\begin{array}{lcl}1+{\log }_{10}count(t,d)& \text{if}& count(t,d)>0\\ 0& & otherwise\end{array}$$由公式得，如果一个词在文档中出现10次，那么tf=2，100次，tf=3。
2. 逆文档频率（inverse document frequency——IDF）：那些只出现在少量文档内的词语可以获得较高权重，这些词对所在的文档具有更高的辨别力。首先给出公式元素定义：文档频率（document frequency-df），$d{f}_t$指的是含有词语t的文档数量。全集词频（collection frequency）指的是词语t在整个语料库中出现的次数。
   还是以莎士比亚的戏剧为例，"Romeo"和action"在莎士比亚语料库中都出现了113次，不过"Romeo"只在一个文档中出现过。故"Romeo"对于所在文档有更高的辨别力，所以我们给Romeo更高的辨别力权重，叫做逆文档频率，或者idf，即：$$id{f}_t={\log }_{10}(\frac{N}{d{f}_t})$$其中N是语料库中文档总数量，$d{f}_t$是含有词语t的文档数量。

  将TF和IDF结合起来构成TF-IDF，表示词语t在文档d中的权值$w_{t,d}$ $$w_{t,d}=t{f}_{t,d}\times id{f}_t$$
  使用TF-IDF将图2的矩阵转换成图6的TF-IDF矩阵。常见词"good"的TF-IDF值变成0，进行文档比较时，忽略"good"同时大大降低了"fool"对文章比较的影响。

图6：TF-IDF矩阵

Word2Vec