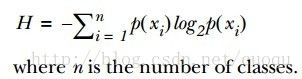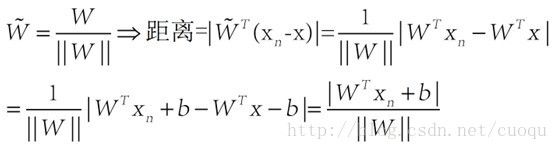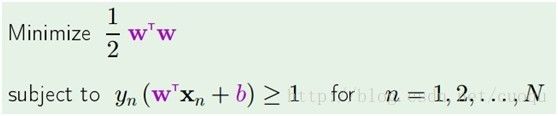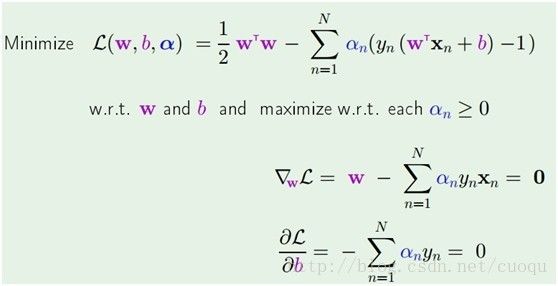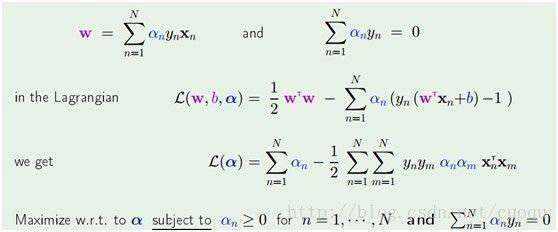chinaliping
chinaliping

机器学习理论与实战

前面的近20篇博文已经牵扯到很多机器学习算法咯，已经吊足了胃口，决定从后面开始正式系统的学习机器学习理论，并尝试进入实战阶段，涵盖：

加州理工(caltech)的 Yaser Abu-Mostafa教授的机器学习，偏重于传统统计理论

斯坦福大学（Staford U)的Andrew Ng教授的机器学习，偏重于实用，直观理解

多伦多大学（Tronto U）的Geoffery Hinton教授的高级神经网络，偏重于神经网络和深度学习

斯坦福大学（Staford U)的Daphne Koller教授的概率图模型，偏重于推理和结构化学习

上面的作为理论指导，以《机器学习实战》（machine learning in action)作为主线，机器学习实战更适合码农，因此这个实用性不言而喻。


机器学习理论与实战（一）K近邻法

  机器学习分两大类，有监督学习(supervised learning)和无监督学习(unsupervised learning)。有监督学习又可分两类：分类（classification.）和回归（regression），分类的任务就是把一个样本划为某个已知类别，每个样本的类别信息在训练时需要给定，比如人脸识别、行为识别、目标检测等都属于分类。回归的任务则是预测一个数值，比如给定房屋市场的数据（面积，位置等样本信息）来预测房价走势。而无监督学习也可以成两类：聚类（clustering）和密度估计（density estimation）,聚类则是把一堆数据聚成弱干组，没有类别信息；密度估计则是估计一堆数据的统计参数信息来描述数据,比如深度学习的RBM。

          根据机器学习实战讲解顺序，先学习K近邻法（K Nearest Neighbors-KNN）

          K近邻法是有监督学习方法，原理很简单，假设我们有一堆分好类的样本数据，分好类表示每个样本都一个对应的已知类标签，当来一个测试样本要我们判断它的类别是，就分别计算到每个样本的距离，然后选取离测试样本最近的前K个样本的标签累计投票，得票数最多的那个标签就为测试样本的标签。

例子（电影分类）：

机器学习理论与实战_第1张图片

（图一）

（图一）中横坐标表示一部电影中的打斗统计个数，纵坐标表示接吻次数。我们要对（图一）中的问号这部电影进行分类，其他几部电影的统计数据和类别如（图二）所示：

机器学习理论与实战_第2张图片

（图二）

从（图二）中可以看出有三部电影的类别是Romance,有三部电影的类别是Action,那如何判断问号表示的这部电影的类别？根据KNN原理,我们需要在（图一）所示的坐标系中计算问号到所有其他电影之间的距离。计算出的欧式距离如（图三）所示：

机器学习理论与实战_第3张图片

（图三）

     由于我们的标签只有两类，那假设我们选K=6/2=3,由于前三个距离最近的电影都是Romance,那么问号表示的电影被判定为Romance。

代码实战（Python版本）：

先来看看KNN的实现：

[python]  view plain copy
  1. from numpy import *  
  2. import operator  
  3. from os import listdir  
  4.   
  5.   
  6. def classify0(inX, dataSet, labels, k):  
  7.     dataSetSize = dataSet.shape[0]    #获取一条样本大小  
  8.     diffMat = tile(inX, (dataSetSize,1)) - dataSet  #计算距离  
  9.     sqDiffMat = diffMat**2    #计算距离  
  10.     sqDistances = sqDiffMat.sum(axis=1)   #计算距离  
  11.     distances = sqDistances**0.5   #计算距离  
  12.     sortedDistIndicies = distances.argsort()  #距离排序  
  13.     classCount={}            
  14.     for i in range(k):  
  15.         voteIlabel = labels[sortedDistIndicies[i]]    #前K个距离最近的投票统计  
  16.         classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1  #前K个距离最近的投票统计  
  17.     sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)  #对投票统计进行排序  
  18.     return sortedClassCount[0][0]   #返回最高投票的类别  

下面取一些样本测试KNN：

[python]  view plain copy
  1. def file2matrix(filename):  
  2.     fr = open(filename)  
  3.     numberOfLines = len(fr.readlines())         #get the number of lines in the file  
  4.     returnMat = zeros((numberOfLines,3))        #prepare matrix to return  
  5.     classLabelVector = []                       #prepare labels return     
  6.     fr = open(filename)  
  7.     index = 0  
  8.     for line in fr.readlines():  
  9.         line = line.strip()  
  10.         listFromLine = line.split('\t')  
  11.         returnMat[index,:] = listFromLine[0:3]  
  12.         classLabelVector.append(int(listFromLine[-1]))  
  13.         index += 1  
  14.     return returnMat,classLabelVector  
  15.       
  16. def autoNorm(dataSet):  
  17.     minVals = dataSet.min(0)  
  18.     maxVals = dataSet.max(0)  
  19.     ranges = maxVals - minVals  
  20.     normDataSet = zeros(shape(dataSet))  
  21.     m = dataSet.shape[0]  
  22.     normDataSet = dataSet - tile(minVals, (m,1))  
  23.     normDataSet = normDataSet/tile(ranges, (m,1))   #element wise divide  
  24.     return normDataSet, ranges, minVals  
  25.      
  26. def datingClassTest():  
  27.     hoRatio = 0.50      #hold out 50%  
  28.     datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')       #load data setfrom file  
  29.     normMat, ranges, minVals = autoNorm(datingDataMat)  
  30.     m = normMat.shape[0]  
  31.     numTestVecs = int(m*hoRatio)  
  32.     errorCount = 0.0  
  33.     for i in range(numTestVecs):  
  34.         classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)  
  35.         print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])  
  36.         if (classifierResult != datingLabels[i]): errorCount += 1.0  
  37.     print "the total error rate is: %f" % (errorCount/float(numTestVecs))  
  38.     print errorCount  

上面的代码中第一个函数从文本文件中读取样本数据，第二个函数把样本归一化，归一化的好处就是降低样本不同特征之间数值量级对距离计算的显著性影响

datingClassTest则是对KNN测试，留了一半数据进行测试，文本文件中的每条数据都有标签，这样可以计算错误率，运行的错误率为：the total error rate is: 0.064000


总结：

优点：高精度，对离群点不敏感，对数据不需要假设模型

缺点：判定时计算量太大，需要大量的内存

工作方式：数值或者类别


下面挑选一步样本数据发出来：

机器学习理论与实战_第4张图片



参考文献：machine learning in action

转载请注明来源：http://blog.csdn.net/cuoqu/article/details/9255377


 

机器学习理论与实战（二）决策树


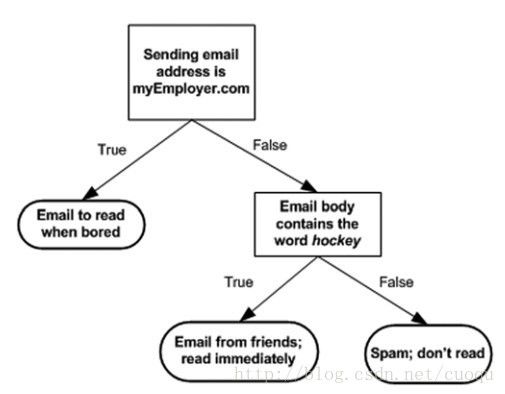
  决策树也是有监督机器学习方法。 电影《无耻混蛋》里有一幕游戏，在德军小酒馆里有几个人在玩20问题游戏，游戏规则是一个设迷者在纸牌中抽出一个目标（可以是人，也可以是物），而猜谜者可以提问题，设迷者只能回答是或者不是，在几个问题（最多二十个问题）之后，猜谜者通过逐步缩小范围就准确的找到了答案。这就类似于决策树的工作原理。（图一）是一个判断邮件类别的工作方式，可以看出判别方法很简单，基本都是阈值判断，关键是如何构建决策树，也就是如何训练一个决策树。

机器学习理论与实战_第5张图片

（图一）

构建决策树的伪代码如下：

Check if every item in the dataset is in the same class:

       If so return the class label

       Else

             find the best feature to split the data

             split the dataset

             create a branch node

             for each split

                    call create Branch and add the result to the branch node

            return branch node

         原则只有一个，尽量使得每个节点的样本标签尽可能少，注意上面伪代码中一句说：find the best feature to split the data，那么如何find thebest feature?一般有个准则就是尽量使得分支之后节点的类别纯一些，也就是分的准确一些。如（图二）中所示，从海洋中捞取的5个动物，我们要判断他们是否是鱼，先用哪个特征？

机器学习理论与实战_第6张图片

（图二）

         

   为了提高识别精度，我们是先用“能否在陆地存活”还是“是否有蹼”来判断？我们必须要有一个衡量准则，常用的有信息论、基尼纯度等，这里使用前者。我们的目标就是选择使得分割后数据集的标签信息增益最大的那个特征，信息增益就是原始数据集标签基熵减去分割后的数据集标签熵，换句话说，信息增益大就是熵变小，使得数据集更有序。熵的计算如（公式一）所示：

（公式一）

       有了指导原则，那就进入代码实战阶段，先来看看熵的计算代码：

[python]  view plain copy
  1. def calcShannonEnt(dataSet):  
  2.     numEntries = len(dataSet)  
  3.     labelCounts = {}  
  4.     for featVec in dataSet: #the the number of unique elements and their occurance  
  5.         currentLabel = featVec[-1]  
  6.         if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0  
  7.         labelCounts[currentLabel] += 1  #收集所有类别的数目，创建字典  
  8.     shannonEnt = 0.0  
  9.     for key in labelCounts:  
  10.         prob = float(labelCounts[key])/numEntries  
  11.         shannonEnt -= prob * log(prob,2) #log base 2  计算熵  
  12.     return shannonEnt  

         有了熵的计算代码，接下来看依照信息增益变大的原则选择特征的代码：


[python]  view plain copy
  1. def splitDataSet(dataSet, axis, value):  
  2.     retDataSet = []  
  3.     for featVec in dataSet:  
  4.         if featVec[axis] == value:  
  5.             reducedFeatVec = featVec[:axis]     #chop out axis used for splitting  
  6.             reducedFeatVec.extend(featVec[axis+1:])  
  7.             retDataSet.append(reducedFeatVec)  
  8.     return retDataSet  
  9.       
  10. def chooseBestFeatureToSplit(dataSet):  
  11.     numFeatures = len(dataSet[0]) - 1      #the last column is used for the labels  
  12.     baseEntropy = calcShannonEnt(dataSet)  
  13.     bestInfoGain = 0.0; bestFeature = -1  
  14.     for i in range(numFeatures):        #iterate over all the features  
  15.         featList = [example[i] for example in dataSet]#create a list of all the examples of this feature  
  16.         uniqueVals = set(featList)       #get a set of unique values  
  17.         newEntropy = 0.0  
  18.         for value in uniqueVals:  
  19.             subDataSet = splitDataSet(dataSet, i, value)  
  20.             prob = len(subDataSet)/float(len(dataSet))  
  21.             newEntropy += prob * calcShannonEnt(subDataSet)       
  22.         infoGain = baseEntropy - newEntropy     #calculate the info gain; ie reduction in entropy  
  23.         if (infoGain > bestInfoGain):       #compare this to the best gain so far    #选择信息增益最大的代码在此  
  24.             bestInfoGain = infoGain         #if better than current best, set to best  
  25.             bestFeature = i  
  26.     return bestFeature                      #returns an integer  

        从最后一个if可以看出，选择使得信息增益最大的特征作为分割特征，现在有了特征分割准则，继续进入一下个环节，如何构建决策树，其实就是依照最上面的伪代码写下去，采用递归的思想依次分割下去，直到执行完成就构建了决策树。代码如下：

[python]  view plain copy
  1. def majorityCnt(classList):  
  2.     classCount={}  
  3.     for vote in classList:  
  4.         if vote not in classCount.keys(): classCount[vote] = 0  
  5.         classCount[vote] += 1  
  6.     sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)  
  7.     return sortedClassCount[0][0]  
  8.   
  9. def createTree(dataSet,labels):  
  10.     classList = [example[-1] for example in dataSet]  
  11.     if classList.count(classList[0]) == len(classList):   
  12.         return classList[0]#stop splitting when all of the classes are equal  
  13.     if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet  
  14.         return majorityCnt(classList)  
  15.     bestFeat = chooseBestFeatureToSplit(dataSet)  
  16.     bestFeatLabel = labels[bestFeat]  
  17.     myTree = {bestFeatLabel:{}}  
  18.     del(labels[bestFeat])  
  19.     featValues = [example[bestFeat] for example in dataSet]  
  20.     uniqueVals = set(featValues)  
  21.     for value in uniqueVals:  
  22.         subLabels = labels[:]       #copy all of labels, so trees don't mess up existing labels  
  23.         myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)  
  24.     return myTree                          

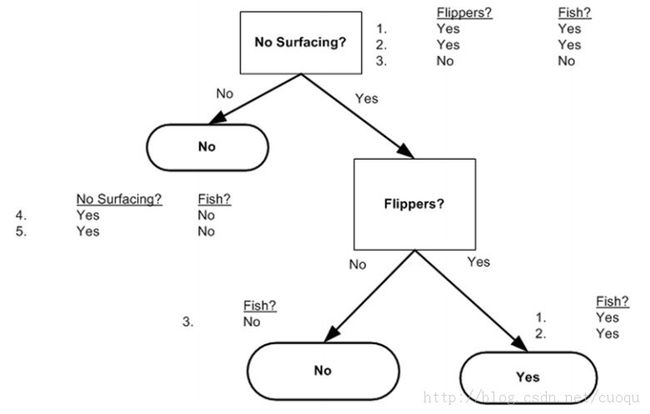
      用图二的样本构建的决策树如（图三）所示：

机器学习理论与实战_第7张图片

（图三）

有了决策树，就可以用它做分类咯，分类代码如下：

[python]  view plain copy
  1. def classify(inputTree,featLabels,testVec):  
  2.     firstStr = inputTree.keys()[0]  
  3.     secondDict = inputTree[firstStr]  
  4.     featIndex = featLabels.index(firstStr)  
  5.     key = testVec[featIndex]  
  6.     valueOfFeat = secondDict[key]  
  7.     if isinstance(valueOfFeat, dict):   
  8.         classLabel = classify(valueOfFeat, featLabels, testVec)  
  9.     else: classLabel = valueOfFeat  
  10.     return classLabel  

最后给出序列化决策树（把决策树模型保存在硬盘上）的代码：

[python]  view plain copy
  1. def storeTree(inputTree,filename):  
  2.     import pickle  
  3.     fw = open(filename,'w')  
  4.     pickle.dump(inputTree,fw)  
  5.     fw.close()  
  6.       
  7. def grabTree(filename):  
  8.     import pickle  
  9.     fr = open(filename)  
  10.     return pickle.load(fr)  
  11.       

优点：检测速度快

缺点：容易过拟合，可以采用修剪的方式来尽量避免

参考文献：machine learning in action


机器学习理论与实战（三）朴素贝叶斯

  贝叶斯决策一直很有争议，今年是贝叶斯250周年，历经沉浮，今天它的应用又开始逐渐活跃，有兴趣的可以看看斯坦福Brad Efron大师对其的反思，两篇文章：“Bayes'Theorem in the 21st Century”和“A250-YEAR ARGUMENT:BELIEF, BEHAVIOR, AND THE BOOTSTRAP”。俺就不参合这事了，下面来看看朴素贝叶斯分类器。

         有时我们想知道给定一个样本时，它属于每个类别的概率是多少,即P(Ci|X),Ci表示类别，X表示测试样本，有了概率后我们可以选择最大的概率的类别。要求这个概率要用经典贝叶斯公式，如（公式一）所示：


（公式一）

         （公式一）中的右边每项一般都是可以计算出的，例如（图一）中两个桶中分别装了黑色（Black）和灰色(Grey)的球。

（图一）

        假设Bucket A和BucketB是类别，C1和C2，当给定一个球时，我们想判断它最可能从哪个桶里出来的，换句话说是什么类别？这就可以根据（公式一）来算，（公式一）的右边部分的每项都可以计算出来，比如P(gray|bucketA)=2/4，P(gray|bucketB)=1/3，更严格的计算方法是:

        P(gray|bucketB) = P(gray andbucketB)/P(bucketB),

        而P(gray and bucketB) = 1/7，P(bucketB)= 3/7

        那么P(gray|bucketB)=P(gray and bucketB)/ P(bucketB)=(1/7)/(3/7)=1/3

      这就是朴素贝叶斯的原理，根据后验概率来判断，选择P(Ci|X)最大的作为X的类别Ci,另外朴素贝叶斯只所以被称为朴素的原因是，它假设了特征之间都是独立的，如（图二）所示：

（图二）

       尽管这个假设很不严密，但是在实际应用中它仍然很有效果，比如文本分类，下面就来看下文本分类实战，判断聊天信息是否是辱骂（abusive）信息(也就是类别为两类，是否辱骂信息)，在此之前，先强调下，朴素贝叶斯的特征向量可以是多维的，上面的公式是一维的，二维的如（公式二）所示，都是相同的计算方法：

（公式二）

       对文本分类，首先的任务就是把文本转成数字向量，也就是提取特征。特征可以说某个关键字在文章中出现的次数(bag of words),比如垃圾邮件中经常出现“公司”，“酬宾”等字样，特征多样，可以根据所需自己建立特征。本例子中采用标记字（token）的方法，标记字可以是任何字符的组合，比如URL,单词，IP地址等，当然判断是否是辱骂信息大多数都是类似于单词的形式。下面来根据代码说下：

首先我们获取一些训练集：

[python]  view plain copy
  1. from numpy import *  
  2.   
  3. def loadDataSet():  
  4.     postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],  
  5.                  ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],  
  6.                  ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],  
  7.                  ['stop', 'posting', 'stupid', 'worthless', 'garbage'],  
  8.                  ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],  
  9.                  ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]  
  10.     classVec = [0,1,0,1,0,1]    #1 is abusive, 0 not  
  11.     return postingList,classVec  

        训练集是从聊天室里摘取的6句话，每句话都有一个标签0或者1，表示是否是辱骂信息（abusive or not abusive）。当然可以把每个消息看成是一个文档，只不过文档单词比这个多，但是一样的道理。接下来处理训练集，看看训练集有多少个不同的（唯一的）单词组成。代码如下：

[python]  view plain copy
  1. def createVocabList(dataSet):  
  2.     vocabSet = set([])  #create empty set  
  3.     for document in dataSet:  
  4.         vocabSet = vocabSet | set(document) #union of the two sets  
  5.     return list(vocabSet)  

        该函数返回一个由唯一单词组成的词汇表。接下来就是特征处理的关键步骤，同样先贴代码：

[python]  view plain copy
  1. def setOfWords2Vec(vocabList, inputSet):  
  2.     returnVec = [0]*len(vocabList)  
  3.     for word in inputSet:  
  4.         if word in vocabList:  
  5.             returnVec[vocabList.index(word)] = 1  
  6.         else: print "the word: %s is not in my Vocabulary!" % word  
  7.     return returnVec  

        这个函数功能：输入词汇表和消息，通过逐个索引词汇表，然后看消息中的是否有对应的字在词汇表中，如果有就标记1，没有就标记0，这样就把每条消息都转成了和词汇表一样长度的有0和1组成的特征向量，如（图三）所示：


（图三）

        有了特征向量，我们就可以训练朴素贝叶斯分类器了，其实就是计算（公式三）右边部分的三个概率，（公式三）如下：

（公式三）

       其中w是特征向量。

代码如下：

[python]  view plain copy
  1. def trainNB0(trainMatrix,trainCategory):  
  2.     numTrainDocs = len(trainMatrix)  
  3.     numWords = len(trainMatrix[0])  
  4.     pAbusive = sum(trainCategory)/float(numTrainDocs)  
  5.     p0Num = ones(numWords); p1Num = ones(numWords)      #change to ones()   
  6.     p0Denom = 2.0; p1Denom = 2.0                        #change to 2.0  
  7.     for i in range(numTrainDocs):  
  8.         if trainCategory[i] == 1:  
  9.             p1Num += trainMatrix[i]  
  10.             p1Denom += sum(trainMatrix[i])  
  11.         else:  
  12.             p0Num += trainMatrix[i]  
  13.             p0Denom += sum(trainMatrix[i])  
  14.     p1Vect = log(p1Num/p1Denom)          #change to log()  
  15.     p0Vect = log(p0Num/p0Denom)          #change to log()  
  16.     return p0Vect,p1Vect,pAbusive  

      上面的代码中输入的是特征向量组成的矩阵，和一个由标签组成的向量，其中pAbusive是类别概率P(ci)，因为只有两类，计算一类后，另外一类可以直接用1-p得出。接下来初始化计算p(wi|c1)和p(wi|c0)的分子和分母，这里惟一让人好奇的就是为什么分母p0Denom和p1Denom都初始化为2？这是因为在实际应用中，我们计算出了（公式三）右半部分的概率后，也就是p(wi|ci)后，注意wi表示消息中的一个字，接下来就是判断整条消息属于某个类别的概率，就要计算p(w0|1)p(w1|1)p(w2|1)的形式，这样如果某个wi为0，这样整个概率都为0，或者都很小连乘后会更小，甚至round off 0。这样就会影响判断，因此把他们转到对数空间中来做运算，对数在机器学习里经常用到，在保持单调的情况下避免因数值运算带来的歧义问题，而且对数可以把乘法转到加法运算，加速了运算。因此上面的代码中把所有的出现次数初始化为1，然后把分母初始为2，接着都是累加，在对数空间中从0还是1开始累加，最后比较大小不会受影响的。

最后贴出分类代码：

[python]  view plain copy
  1. def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):  
  2.     p1 = sum(vec2Classify * p1Vec) + log(pClass1)    #element-wise mult  
  3.     p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)  
  4.     if p1 > p0:  
  5.         return 1  
  6.     else:   
  7.         return 0  

     分类代码也是在对数空间中计算的后验概率，然后通过比较大小来判断消息属于那一类。


总结：

       优点：对小量数据很有效，可以处理多类

       缺点：很依赖于数据的准备

朴素贝叶斯在概率图模型里被划为判别模型（Discriminative model)


参考文献：

         [1] Machine learning in action.Peter Harrington 

         [2]Probabilistic graphical model.Daphne Koller

机器学习理论与实战（四）逻辑回归

   从这节算是开始进入“正规”的机器学习了吧，之所以“正规”因为它开始要建立价值函数（cost function），接着优化价值函数求出权重，然后测试验证。这整套的流程是机器学习必经环节。今天要学习的话题是逻辑回归，逻辑回归也是一种有监督学习方法（supervised machine learning）。逻辑回归一般用来做预测，也可以用来做分类，预测是某个类别^.^！线性回归想比大家都不陌生了，y=kx+b,给定一堆数据点，拟合出k和b的值就行了，下次给定X时，就可以计算出y,这就是回归。而逻辑回归跟这个有点区别，它是一种非线性函数，拟合功能颇为强大，而且它是连续函数，可以对其求导，这点很重要，如果一个函数不可求导，那它在机器学习用起来很麻烦，早期的海维赛德（Heaviside）阶梯函数就因此被sigmoid函数取代，因为可导意味着我们可以很快找到其极值点，这就是优化方法的重要思想之一：利用求导，得到梯度，然后用梯度下降法更新参数。

        下面来看看逻辑回归的sigmoid函数，如（图一）所示：


（图一）

            （图一）中上图是sigmoid函数在定义域[-5,5] 上的形状，而下图是在定义域[-60,60]上的形状，由这两个图可以看出，它比较适合做二类的回归，因为严重两级分化。Sigmoid函数的如（公式一）所示：

（公式一）

         现在有了二类回归函数模型，就可以把特征映射到这个模型上了，而且sigmoid函数的自变量只有一个Z，假设我们的特征为X=[x0,x1,x2…xn]。令

，当给定大批的训练样本特征X时，我们只要找到合适的W=[w0,w1,w2…wn]来正确的把每个样本特征X映射到sigmoid函数的两级上，也就是说正确的完成了类别回归就行了，那么以后来个测试样本，只要和权重相乘后，带入sigmoid函数计算出的值就是预测值啦，很简单是吧。那怎么求权重W呢？

          要计算W，就要进入优化求解阶段咯，用的方法是梯度下降法或者随机梯度下降法。说到梯度下降，梯度下降一般对什么求梯度呢？梯度是一个函数上升最快的方向，沿着梯度方向我们可以很快找到极值点。我们找什么极值？仔细想想，当然是找训练模型的误差极值，当模型预测值和训练样本给出的正确值之间的误差和最小时，模型参数就是我们要求的。当然误差最小有可能导致过拟合，这个以后再说。我们先建立模型训练误差价值函数（cost function），如（公式二）所示：

（公式二）

        （公式二）中Y表示训练样本真实值，当J（theta）最小时的所得的theta就是我们要求的模型权重，可以看出J(theta)是个凸函数，得到的最小值也是全局最小。对其求导后得出梯度，如（公式三）所示：

（公式三）

        由于我们是找极小值，而梯度方向是极大值方向，因此我们取负号，沿着负梯度方向更新参数，如（公式四）所示：

（公式四）

        按照（公式四）的参数更新方法，当权重不再变化时，我们就宣称找到了极值点，此时的权重也是我们要求的，整个参数更新示意图如（图二）所示：

（图二）

        原理到此为止逻辑回归基本就说完了，下面进入代码实战阶段：


[python]  view plain copy
  1. from numpy import *  
  2.   
  3. def loadDataSet():  
  4.     dataMat = []; labelMat = []  
  5.     fr = open('testSet.txt')  
  6.     for line in fr.readlines():  
  7.         lineArr = line.strip().split()  
  8.         dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])  
  9.         labelMat.append(int(lineArr[2]))  
  10.     return dataMat,labelMat  
  11.   
  12. def sigmoid(inX):  
  13.     return 1.0/(1+exp(-inX))  

上面两个函数分别是加载训练集和定义sigmoid函数，都比较简单。下面发出梯度下降的代码：

[python]  view plain copy
  1. def gradAscent(dataMatIn, classLabels):  
  2.     dataMatrix = mat(dataMatIn)             #convert to NumPy matrix  
  3.     labelMat = mat(classLabels).transpose() #convert to NumPy matrix  
  4.     m,n = shape(dataMatrix)  
  5.     alpha = 0.001  
  6.     maxCycles = 500  
  7.     weights = ones((n,1))  
  8.     for k in range(maxCycles):              #heavy on matrix operations  
  9.         h = sigmoid(dataMatrix*weights)     #matrix mult  
  10.         error = (labelMat - h)              #vector subtraction  
  11.         weights = weights + alpha * dataMatrix.transpose()* error #matrix mult  
  12.     return weights  

         梯度下降输入训练集和对应标签，接着就是迭代跟新参数，计算梯度，然后更新参数，注意倒数第二句就是按照（公式三）和（公式四）来更新参数。

为了直观的看到我们得到的权重是否正确的，我们把权重和样本打印出来，下面是相关打印代码：

[python]  view plain copy
  1. def plotBestFit(weights):  
  2.     import matplotlib.pyplot as plt  
  3.     dataMat,labelMat=loadDataSet()  
  4.     dataArr = array(dataMat)  
  5.     n = shape(dataArr)[0]   
  6.     xcord1 = []; ycord1 = []  
  7.     xcord2 = []; ycord2 = []  
  8.     for i in range(n):  
  9.         if int(labelMat[i])== 1:  
  10.             xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])  
  11.         else:  
  12.             xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])  
  13.     fig = plt.figure()  
  14.     ax = fig.add_subplot(111)  
  15.     ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')  
  16.     ax.scatter(xcord2, ycord2, s=30, c='green')  
  17.     x = arange(-3.0, 3.0, 0.1)  
  18.     y = (-weights[0]-weights[1]*x)/weights[2]  
  19.     ax.plot(x, y)  
  20.     plt.xlabel('X1'); plt.ylabel('X2');  
  21.     plt.show()  

打印的效果图如（图三）所示：

（图三）

       可以看出效果蛮不错的，小错误是难免的，如果训练集没有错误反而危险，说到这基本就说完了，但是考虑到这个方法对少量样本（几百的）还行，在实际中当遇到10亿数量级时，而且特征维数上千时，这种方法很恐怖，光计算梯度就要消耗大量时间，因此要使用随机梯度下降方法。随机梯度下降算法和梯度下降算法原理一样，只是计算梯度不再使用所有样本，而是使用一个或者一小批来计算梯度，这样可以减少计算代价，虽然权重更新的路径很曲折，但最终也会收敛的，如（图四）所示


（图四）

       下面也发出随机梯度下降的代码：

[python]  view plain copy
  1. def stocGradAscent1(dataMatrix, classLabels, numIter=150):  
  2.     m,n = shape(dataMatrix)  
  3.     weights = ones(n)   #initialize to all ones  
  4.     for j in range(numIter):  
  5.         dataIndex = range(m)  
  6.         for i in range(m):  
  7.             alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not   
  8.             randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant  
  9.             h = sigmoid(sum(dataMatrix[randIndex]*weights))  
  10.             error = classLabels[randIndex] - h  
  11.             weights = weights + alpha * error * dataMatrix[randIndex]  
  12.             del(dataIndex[randIndex])  
  13.     return weights  

       最后也给出一个分类的代码，只要把阈值设为0.5，大于0.5划为一类，小于0.5划为另一类就行了，代码如下：

[python]  view plain copy
  1. def classifyVector(inX, weights):  
  2.     prob = sigmoid(sum(inX*weights))  
  3.     if prob > 0.5: return 1.0  
  4.     else: return 0.0  

总结：

        优点：计算量不高，容易实现，对现实数据也很容易描述

        缺点：很容易欠拟合，精度可能也会不高

参考文献：

    [1] machine learning in action. Peter Harrington

    [2] machine learning.Andrew Ng


机器学习理论与实战（五）支持向量机

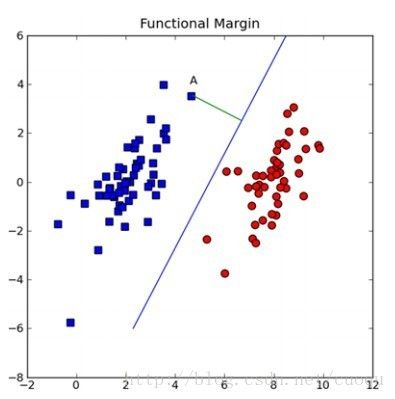
   做机器学习的一定对支持向量机（support vector machine-SVM）颇为熟悉，因为在深度学习出现之前，SVM一直霸占着机器学习老大哥的位子。他的理论很优美，各种变种改进版本也很多，比如latent-SVM, structural-SVM等。这节先来看看SVM的理论吧，在（图一）中A图表示有两类的数据集，图B,C,D都提供了一个线性分类器来对数据进行分类？但是哪个效果好一些？


（图一）

        可能对这个数据集来说，三个的分类器都一样足够好了吧，但是其实不然，这个只是训练集，现实测试的样本分布可能会比较散一些，各种可能都有，为了应对这种情况，我们要做的就是尽可能的使得线性分类器离两个数据集都尽可能的远，因为这样就会减少现实测试样本越过分类器的风险，提高检测精度。这种使得数据集到分类器之间的间距（margin）最大化的思想就是支持向量机的核心思想，而离分类器距离最近的样本成为支持向量。既然知道了我们的目标就是为了寻找最大边距，怎么寻找支持向量？如何实现？下面以（图二）来说明如何完成这些工作。

机器学习理论与实战_第8张图片

（图二）

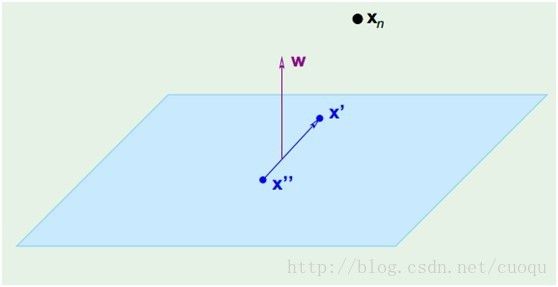
假设（图二）中的直线表示一个超面，为了方面观看显示成一维直线，特征都是超面维度加一维度的，图中也可以看出，特征是二维，而分类器是一维的。如果特征是三维的，分类器就是一个平面。假设超面的解析式为 ，那么点A到超面的距离为 ,下面给出这个距离证明：

机器学习理论与实战_第9张图片

（图三）

在（图三）中，青色菱形表示超面，Xn为数据集中一点，W是超面权重，而且W是垂直于超面的。证明垂直很简单，假设X’和X’’都是超面上的一点，

机器学习理论与实战_第10张图片

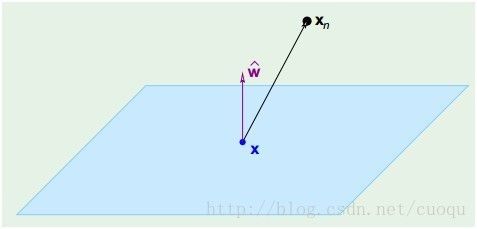
,因此W垂直于超面。知道了W垂直于超面，那么Xn到超面的距离其实就是Xn和超面上任意一点x的连线在W上的投影，如（图四）所示：

机器学习理论与实战_第11张图片

（图四）

而（Xn-X）在W上的投影可通过（公式一）来计算，另外（公式一）也一并完成距离计算：

机器学习理论与实战_第12张图片

（公式一）

     注意最后使用了配项法并且用了超面解析式 才得出了距离计算。有了距离就可以来推导我们刚开始的想法：使得分类器距所有样本距离最远，即最大化边距，但是最大化边距的前提是我们要找到支持向量，也就是离分类器最近的样本点，此时我们就要完成两个优化任务，找到离分类器最近的点（支持向量），然后最大化边距。如（公式二）所示：
机器学习理论与实战_第13张图片

（公式二）

        大括号里面表示找到距离分类超面最近的支持向量，大括号外面则是使得超面离支持向量的距离最远，要优化这个函数相当困难，目前没有太有效的优化方法。但是我们可以把问题转换一下，如果我们把 大括号里面的优化问题固定住 ，然后来优化外面的就很容易了，可以用现在的优化方法来求解，因此我们做一个假设，假设大括号里的分子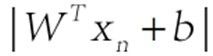 等于1，那么我们只剩下优化W咯，整个优化公式就可以写成（公式三）的形式：

机器学习理论与实战_第14张图片

（公式三）

        这下就简单了，有等式约束的优化，约束式子为 ，这个约束等式背后还有个小窍门，假设我们把样本 Xn 的标签设为 1 或者 -1 ，当 Xn 在超面上面（或者右边）时，带入超面解析式得到大于 0 的值，乘上标签 1 仍然为本身，可以表示离超面的距离；当 Xn 在超面下面（或者左边）时，带入超面解析式得到小于 0 的值，乘上标签 -1 也是正值，仍然可以表示距离，因此我们把通常两类的标签 0 和 1 转换成 -1 和 1 就可以把标签信息完美的融进等式约束中，（公式三）最后一行也体现出来咯。下面继续说优化 求解（公式四）的方法，在最优化中，通常我们需要求解的最优化问题有如下几类：

       (i)无约束优化问题，可以写为:

              min f(x);  

       (ii)有等式约束的优化问题，可以写为:

                  min f(x), 

                   s.t. h_i(x) = 0; i =1, ..., n 

        (iii)有不等式约束的优化问题，可以写为：

                min f(x), 

                 s.t. g_i(x) <= 0; i =1, ..., n

                h_j(x) = 0; j =1,..., m

       对于第(i)类的优化问题，常常使用的方法就是Fermat定理，即使用求取f(x)的导数，然后令其为零，可以求得候选最优值，再在这些候选值中验证；如果是凸函数，可以保证是最优解。

       对于第(ii)类的优化问题，常常使用的方法就是拉格朗日乘子法（LagrangeMultiplier)，即把等式约束h_i(x)用一个系数与f(x)写为一个式子，称为拉格朗日函数，而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导，令其为零，可以求得候选值集合，然后验证求得最优值。

       对于第(iii)类的优化问题，常常使用的方法就是KKT条件。同样地，我们把所有的等式、不等式约束与f(x)写为一个式子，也叫拉格朗日函数，系数也称拉格朗日乘子，通过一些条件，可以求出最优值的必要条件，这个条件称为KKT条件。

       而（公式三）很明显符合第二类优化方法，因此可以使用拉格朗日乘子法来对其求解，在求解之前，我们先对（公式四）做个简单的变换。最大化||W||的导数可以最小化||W||或者W’W，如（公式四）所示：

机器学习理论与实战_第15张图片

（公式四）

套进拉格朗日乘子法公式得到如（公式五）所示的样子：


机器学习理论与实战_第16张图片

（公式五）

        在（公式五）中通过拉格朗日乘子法函数分别对W和b求导，为了得到极值点，令导数为0，得到


 ,然后把他们代入拉格朗日乘子法公式里得到（公式六）的形式：

机器学习理论与实战_第17张图片

（公式六）

     （公式六）后两行是目前我们要求解的优化函数，现在只需要做个二次规划即可求出alpha,二次规划优化求解如（公式七）所示：


机器学习理论与实战_第18张图片

（公式七）

         通过（公式七）求出alpha后，就可以用（公式六）中的第一行求出W。到此为止，SVM的公式推导基本完成了，可以看出数学理论很严密，很优美，尽管有些同行们认为看起枯燥，但是最好沉下心来从头看完，也不难，难的是优化。二次规划求解计算量很大，在实际应用中常用SMO（Sequential minimal optimization）算法，SMO算法打算放在下节结合代码来说。


参考文献：

     [1]machine learning in action. Peter Harrington

     [2] Learning From Data. Yaser S.Abu-Mostafa

   

机器学习理论与实战（六）支持向量机

  上节基本完成了SVM的理论推倒，寻找最大化间隔的目标最终转换成求解拉格朗日乘子变量alpha的求解问题，求出了alpha即可求解出SVM的权重W，有了权重也就有了最大间隔距离，但是其实上节我们有个假设：就是训练集是线性可分的，这样求出的alpha在[0,infinite]。但是如果数据不是线性可分的呢？此时我们就要允许部分的样本可以越过分类器，这样优化的目标函数就可以不变，只要引入松弛变量即可，它表示错分类样本点的代价，分类正确时它等于0，当分类错误时，其中Tn表示样本的真实标签-1或者1，回顾上节中，我们把支持向量到分类器的距离固定为1，因此两类的支持向量间的距离肯定大于1的，当分类错误时肯定也大于1，如（图五）所示（这里公式和图标序号都接上一节）。


（图五）

       这样有了错分类的代价，我们把上节（公式四）的目标函数上添加上这一项错分类代价，得到如（公式八）的形式：

（公式八）

        重复上节的拉格朗日乘子法步骤，得到（公式九）：

（公式九）

         多了一个Un乘子，当然我们的工作就是继续求解此目标函数，继续重复上节的步骤，求导得到（公式十）：


（公式十）

         又因为alpha大于0，而且Un大于0，所以0注意Un是大于等于0：

       推导到现在，优化函数的形式基本没变，只是多了一项错分类的价值，但是多了一个条件，0

（图六）

         在（图六）中，现有的样本是很明显线性不可分，但是加入我们利用现有的样本X之间作些不同的运算，如（图六）右边所示的样子，而让f作为新的样本（或者说新的特征）是不是更好些？现在把X已经投射到高维度上去了，但是f我们不知道，此时核函数就该上场了，以高斯核函数为例，在（图七）中选几个样本点作为基准点，来利用核函数计算f,如（图七）所示：

（图七）

       这样就有了f,而核函数此时相当于对样本的X和基准点一个度量，做权重衰减，形成依赖于x的新的特征f,把f放在上面说的SVM中继续求解alpha，然后得出权重就行了，原理很简单吧，为了显得有点学术味道，把核函数也做个样子加入目标函数中去吧，如（公式十一）所示：


（公式十一）


        其中K(Xn,Xm)是核函数，和上面目标函数比没有多大的变化，用SMO优化求解就行了，代码如下：

[python]  view plain copy
  1. def smoPK(dataMatIn, classLabels, C, toler, maxIter):    #full Platt SMO  
  2.     oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler)  
  3.     iter = 0  
  4.     entireSet = True; alphaPairsChanged = 0  
  5.     while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):  
  6.         alphaPairsChanged = 0  
  7.         if entireSet:   #go over all  
  8.             for i in range(oS.m):          
  9.                 alphaPairsChanged += innerL(i,oS)  
  10.                 print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)  
  11.             iter += 1  
  12.         else:#go over non-bound (railed) alphas  
  13.             nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]  
  14.             for i in nonBoundIs:  
  15.                 alphaPairsChanged += innerL(i,oS)  
  16.                 print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)  
  17.             iter += 1  
  18.         if entireSet: entireSet = False #toggle entire set loop  
  19.         elif (alphaPairsChanged == 0): entireSet = True    
  20.         print "iteration number: %d" % iter  
  21.     return oS.b,oS.alphas  

       下面演示一个小例子，手写识别。

      (1)收集数据：提供文本文件

      (2)准备数据：基于二值图像构造向量

      (3)分析数据：对图像向量进行目测

      (4)训练算法：采用两种不同的核函数，并对径向基函数采用不同的设置来运行SMO算法。

       (5)测试算法：编写一个函数来测试不同的核函数，并计算错误率

       (6)使用算法：一个图像识别的完整应用还需要一些图像处理的只是，此demo略。

      完整代码如下：

[python]  view plain copy
  1. from numpy import *  
  2. from time import sleep  
  3.   
  4. def loadDataSet(fileName):  
  5.     dataMat = []; labelMat = []  
  6.     fr = open(fileName)  
  7.     for line in fr.readlines():  
  8.         lineArr = line.strip().split('\t')  
  9.         dataMat.append([float(lineArr[0]), float(lineArr[1])])  
  10.         labelMat.append(float(lineArr[2]))  
  11.     return dataMat,labelMat  
  12.   
  13. def selectJrand(i,m):  
  14.     j=i #we want to select any J not equal to i  
  15.     while (j==i):  
  16.         j = int(random.uniform(0,m))  
  17.     return j  
  18.   
  19. def clipAlpha(aj,H,L):  
  20.     if aj > H:   
  21.         aj = H  
  22.     if L > aj:  
  23.         aj = L  
  24.     return aj  
  25.   
  26. def smoSimple(dataMatIn, classLabels, C, toler, maxIter):  
  27.     dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()  
  28.     b = 0; m,n = shape(dataMatrix)  
  29.     alphas = mat(zeros((m,1)))  
  30.     iter = 0  
  31.     while (iter < maxIter):  
  32.         alphaPairsChanged = 0  
  33.         for i in range(m):  
  34.             fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b  
  35.             Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions  
  36.             if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):  
  37.                 j = selectJrand(i,m)  
  38.                 fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b  
  39.                 Ej = fXj - float(labelMat[j])  
  40.                 alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();  
  41.                 if (labelMat[i] != labelMat[j]):  
  42.                     L = max(0, alphas[j] - alphas[i])  
  43.                     H = min(C, C + alphas[j] - alphas[i])  
  44.                 else:  
  45.                     L = max(0, alphas[j] + alphas[i] - C)  
  46.                     H = min(C, alphas[j] + alphas[i])  
  47.                 if L==H: print "L==H"; continue  
  48.                 eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T  
  49.                 if eta >= 0: print "eta>=0"; continue  
  50.                 alphas[j] -= labelMat[j]*(Ei - Ej)/eta  
  51.                 alphas[j] = clipAlpha(alphas[j],H,L)  
  52.                 if (abs(alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; continue  
  53.                 alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j  
  54.                                                                         #the update is in the oppostie direction  
  55.                 b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T  
  56.                 b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T  
  57.                 if (0 < alphas[i]) and (C > alphas[i]): b = b1  
  58.                 elif (0 < alphas[j]) and (C > alphas[j]): b = b2  
  59.                 else: b = (b1 + b2)/2.0  
  60.                 alphaPairsChanged += 1  
  61.                 print "iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)  
  62.         if (alphaPairsChanged == 0): iter += 1  
  63.         else: iter = 0  
  64.         print "iteration number: %d" % iter  
  65.     return b,alphas  
  66.   
  67. def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space  
  68.     m,n = shape(X)  
  69.     K = mat(zeros((m,1)))  
  70.     if kTup[0]=='lin': K = X * A.T   #linear kernel  
  71.     elif kTup[0]=='rbf':  
  72.         for j in range(m):  
  73.             deltaRow = X[j,:] - A  
  74.             K[j] = deltaRow*deltaRow.T  
  75.         K = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab  
  76.     else: raise NameError('Houston We Have a Problem -- \  
  77.     That Kernel is not recognized')  
  78.     return K  
  79.   
  80. class optStruct:  
  81.     def __init__(self,dataMatIn, classLabels, C, toler, kTup):  # Initialize the structure with the parameters   
  82.         self.X = dataMatIn  
  83.         self.labelMat = classLabels  
  84.         self.C = C  
  85.         self.tol = toler  
  86.         self.m = shape(dataMatIn)[0]  
  87.         self.alphas = mat(zeros((self.m,1)))  
  88.         self.b = 0  
  89.         self.eCache = mat(zeros((self.m,2))) #first column is valid flag  
  90.         self.K = mat(zeros((self.m,self.m)))  
  91.         for i in range(self.m):  
  92.             self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)  
  93.           
  94. def calcEk(oS, k):  
  95.     fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)  
  96.     Ek = fXk - float(oS.labelMat[k])  
  97.     return Ek  
  98.           
  99. def selectJ(i, oS, Ei):         #this is the second choice -heurstic, and calcs Ej  
  100.     maxK = -1; maxDeltaE = 0; Ej = 0  
  101.     oS.eCache[i] = [1,Ei]  #set valid #choose the alpha that gives the maximum delta E  
  102.     validEcacheList = nonzero(oS.eCache[:,0].A)[0]  
  103.     if (len(validEcacheList)) > 1:  
  104.         for k in validEcacheList:   #loop through valid Ecache values and find the one that maximizes delta E  
  105.             if k == i: continue #don't calc for i, waste of time  
  106.             Ek = calcEk(oS, k)  
  107.             deltaE = abs(Ei - Ek)  
  108.             if (deltaE > maxDeltaE):  
  109.                 maxK = k; maxDeltaE = deltaE; Ej = Ek  
  110.         return maxK, Ej  
  111.     else:   #in this case (first time around) we don't have any valid eCache values  
  112.         j = selectJrand(i, oS.m)  
  113.         Ej = calcEk(oS, j)  
  114.     return j, Ej  
  115.   
  116. def updateEk(oS, k):#after any alpha has changed update the new value in the cache  
  117.     Ek = calcEk(oS, k)  
  118.     oS.eCache[k] = [1,Ek]  
  119.           
  120. def innerL(i, oS):  
  121.     Ei = calcEk(oS, i)  
  122.     if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):  
  123.         j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand  
  124.         alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();  
  125.         if (oS.labelMat[i] != oS.labelMat[j]):  
  126.             L = max(0, oS.alphas[j] - oS.alphas[i])  
  127.             H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])  
  128.         else:  
  129.             L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)  
  130.             H = min(oS.C, oS.alphas[j] + oS.alphas[i])  
  131.         if L==H: print "L==H"; return 0  
  132.         eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel  
  133.         if eta >= 0: print "eta>=0"; return 0  
  134.         oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta  
  135.         oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)  
  136.         updateEk(oS, j) #added this for the Ecache  
  137.         if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0  
  138.         oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j  
  139.         updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction  
  140.         b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]  
  141.         b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]  
  142.         if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1  
  143.         elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2  
  144.         else: oS.b = (b1 + b2)/2.0  
  145.         return 1  
  146.     else: return 0  
  147.   
  148. def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):    #full Platt SMO  
  149.     oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)  
  150.     iter = 0  
  151.     entireSet = True; alphaPairsChanged = 0  
  152.     while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):  
  153.         alphaPairsChanged = 0  
  154.         if entireSet:   #go over all  
  155.             for i in range(oS.m):          
  156.                 alphaPairsChanged += innerL(i,oS)  
  157.                 print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)  
  158.             iter += 1  
  159.         else:#go over non-bound (railed) alphas  
  160.             nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]  
  161.             for i in nonBoundIs:  
  162.                 alphaPairsChanged += innerL(i,oS)  
  163.                 print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)  
  164.             iter += 1  
  165.         if entireSet: entireSet = False #toggle entire set loop  
  166.         elif (alphaPairsChanged == 0): entireSet = True    
  167.         print "iteration number: %d" % iter  
  168.     return oS.b,oS.alphas  
  169.   
  170. def calcWs(alphas,dataArr,classLabels):  
  171.     X = mat(dataArr); labelMat = mat(classLabels).transpose()  
  172.     m,n = shape(X)  
  173.     w = zeros((n,1))  
  174.     for i in range(m):  
  175.         w += multiply(alphas[i]*labelMat[i],X[i,:].T)  
  176.     return w  
  177.   
  178. def testRbf(k1=1.3):  
  179.     dataArr,labelArr = loadDataSet('testSetRBF.txt')  
  180.     b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important  
  181.     datMat=mat(dataArr); labelMat = mat(labelArr).transpose()  
  182.     svInd=nonzero(alphas.A>0)[0]  
  183.     sVs=datMat[svInd] #get matrix of only support vectors  
  184.     labelSV = labelMat[svInd];  
  185.     print "there are %d Support Vectors" % shape(sVs)[0]  
  186.     m,n = shape(datMat)  
  187.     errorCount = 0  
  188.     for i in range(m):  
  189.         kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))  
  190.         predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b  
  191.         if sign(predict)!=sign(labelArr[i]): errorCount += 1  
  192.     print "the training error rate is: %f" % (float(errorCount)/m)  
  193.     dataArr,labelArr = loadDataSet('testSetRBF2.txt')  
  194.     errorCount = 0  
  195.     datMat=mat(dataArr); labelMat = mat(labelArr).transpose()  
  196.     m,n = shape(datMat)  
  197.     for i in range(m):  
  198.         kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))  
  199.         predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b  
  200.         if sign(predict)!=sign(labelArr[i]): errorCount += 1      
  201.     print "the test error rate is: %f" % (float(errorCount)/m)      
  202.       
  203. def img2vector(filename):  
  204.     returnVect = zeros((1,1024))  
  205.     fr = open(filename)  
  206.     for i in range(32):  
  207.         lineStr = fr.readline()  
  208.         for j in range(32):  
  209.             returnVect[0,32*i+j] = int(lineStr[j])  
  210.     return returnVect  
  211.   
  212. def loadImages(dirName):  
  213.     from os import listdir  
  214.     hwLabels = []  
  215.     trainingFileList = listdir(dirName)           #load the training set  
  216.     m = len(trainingFileList)  
  217.     trainingMat = zeros((m,1024))  
  218.     for i in range(m):  
  219.         fileNameStr = trainingFileList[i]  
  220.         fileStr = fileNameStr.split('.')[0]     #take off .txt  
  221.         classNumStr = int(fileStr.split('_')[0])  
  222.         if classNumStr == 9: hwLabels.append(-1)  
  223.         else: hwLabels.append(1)  
  224.         trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))  
  225.     return trainingMat, hwLabels      
  226.   
  227. def testDigits(kTup=('rbf', 10)):  
  228.     dataArr,labelArr = loadImages('trainingDigits')  
  229.     b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)  
  230.     datMat=mat(dataArr); labelMat = mat(labelArr).transpose()  
  231.     svInd=nonzero(alphas.A>0)[0]  
  232.     sVs=datMat[svInd]   
  233.     labelSV = labelMat[svInd];  
  234.     print "there are %d Support Vectors" % shape(sVs)[0]  
  235.     m,n = shape(datMat)  
  236.     errorCount = 0  
  237.     for i in range(m):  
  238.         kernelEval = kernelTrans(sVs,datMat[i,:],kTup)  
  239.         predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b  
  240.         if sign(predict)!=sign(labelArr[i]): errorCount += 1  
  241.     print "the training error rate is: %f" % (float(errorCount)/m)  
  242.     dataArr,labelArr = loadImages('testDigits')  
  243.     errorCount = 0  
  244.     datMat=mat(dataArr); labelMat = mat(labelArr).transpose()  
  245.     m,n = shape(datMat)  
  246.     for i in range(m):  
  247.         kernelEval = kernelTrans(sVs,datMat[i,:],kTup)  
  248.         predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b  
  249.         if sign(predict)!=sign(labelArr[i]): errorCount += 1      
  250.     print "the test error rate is: %f" % (float(errorCount)/m)   
  251.   
  252.   
  253. '''''#######******************************** 
  254. Non-Kernel VErsions below 
  255. '''#######********************************  
  256.   
  257. class optStructK:  
  258.     def __init__(self,dataMatIn, classLabels, C, toler):  # Initialize the structure with the parameters   
  259.         self.X = dataMatIn  
  260.         self.labelMat = classLabels  
  261.         self.C = C  
  262.         self.tol = toler  
  263.         self.m = shape(dataMatIn)[0]  
  264.         self.alphas = mat(zeros((self.m,1)))  
  265.         self.b = 0  
  266.         self.eCache = mat(zeros((self.m,2))) #first column is valid flag  
  267.           
  268. def calcEkK(oS, k):  
  269.     fXk = float(multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b  
  270.     Ek = fXk - float(oS.labelMat[k])  
  271.     return Ek  
  272.           
  273. def selectJK(i, oS, Ei):         #this is the second choice -heurstic, and calcs Ej  
  274.     maxK = -1; maxDeltaE = 0; Ej = 0  
  275.     oS.eCache[i] = [1,Ei]  #set valid #choose the alpha that gives the maximum delta E  
  276.     validEcacheList = nonzero(oS.eCache[:,0].A)[0]  
  277.     if (len(validEcacheList)) > 1:  
  278.         for k in validEcacheList:   #loop through valid Ecache values and find the one that maximizes delta E  
  279.             if k == i: continue #don't calc for i, waste of time  
  280.             Ek = calcEk(oS, k)  
  281.             deltaE = abs(Ei - Ek)  
  282.             if (deltaE > maxDeltaE):  
  283.                 maxK = k; maxDeltaE = deltaE; Ej = Ek  
  284.         return maxK, Ej  
  285.     else:   #in this case (first time around) we don't have any valid eCache values  
  286.         j = selectJrand(i, oS.m)  
  287.         Ej = calcEk(oS, j)  
  288.     return j, Ej  
  289.   
  290. def updateEkK(oS, k):#after any alpha has changed update the new value in the cache  
  291.     Ek = calcEk(oS, k)  
  292.     oS.eCache[k] = [1,Ek]  
  293.           
  294. def innerLK(i, oS):  
  295.     Ei = calcEk(oS, i)  
  296.     if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):  
  297.         j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand  
  298.         alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();  
  299.         if (oS.labelMat[i] != oS.labelMat[j]):  
  300.             L = max(0, oS.alphas[j] - oS.alphas[i])  
  301.             H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])  
  302.         else:  
  303.             L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)  
  304.             H = min(oS.C, oS.alphas[j] + oS.alphas[i])  
  305.         if L==H: print "L==H"; return 0  
  306.         eta = 2.0 * oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T  
  307.         if eta >= 0: print "eta>=0"; return 0  
  308.         oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta  
  309.         oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)  
  310.         updateEk(oS, j) #added this for the Ecache  
  311.         if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0  
  312.         oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j  
  313.         updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction  
  314.         b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T  
  315.         b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T  
  316.         if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1  
  317.         elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2  
  318.         else: oS.b = (b1 + b2)/2.0  
  319.         return 1  
  320.     else: return 0  
  321.   
  322. def smoPK(dataMatIn, classLabels, C, toler, maxIter):    #full Platt SMO  
  323.     oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler)  
  324.     iter = 0  
  325.     entireSet = True; alphaPairsChanged = 0  
  326.     while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):  
  327.         alphaPairsChanged = 0  
  328.         if entireSet:   #go over all  
  329.             for i in range(oS.m):          
  330.                 alphaPairsChanged += innerL(i,oS)  
  331.                 print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)  
  332.             iter += 1  
  333.         else:#go over non-bound (railed) alphas  
  334.             nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]  
  335.             for i in nonBoundIs:  
  336.                 alphaPairsChanged += innerL(i,oS)  
  337.                 print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)  
  338.             iter += 1  
  339.         if entireSet: entireSet = False #toggle entire set loop  
  340.         elif (alphaPairsChanged == 0): entireSet = True    
  341.         print "iteration number: %d" % iter  
  342.     return oS.b,oS.alphas  

运行结果如（图八）所示：


（图八）

上面代码有兴趣的可以读读，用的话，建议使用libsvm。

参考文献：

    [1]machine learning in action. PeterHarrington

    [2] pattern recognition and machinelearning. Christopher M. Bishop

    [3]machine learning.Andrew Ng


机器学习理论与实战（七）Adaboost

 Adaboost也是一种原理简单，但很实用的有监督机器学习算法，它是daptive boosting的简称。说到boosting算法，就不得提一提bagging算法，他们两个都是把一些弱分类器组合起来来进行分类的方法，统称为集成方法（ensemble method）,类似于投资，“不把鸡蛋放在一个篮子”，虽然每个弱分类器分类的不那么准确，但是如果把多个弱分类器组合起来可以得到相当不错的结果，另外要说的是集成方法还可以组合不同的分类器，而Adaboost和boosting算法的每个弱分类器的类型都一样的。他们两个不同的地方是：boosting的每个弱分类器组合起来的权重不一样，本节的Adaboost就是一个例子，而bagging的每个弱分类器的组合权重是相等，代表的例子就是random forest。Random forest的每个弱分类器是决策树，输出的类别有多个决策树分类的类别的众数决定。今天的主题是Adaboost,下面来看看Adaboost的工作原理：

         既然Adaboost的每个弱分类器的类型都一样，那么怎么组织安排每个分类器呢？如（图一）所示：


（图一）

       （图一）是Adaboost的原理示意图，左边矩形表示数据集，中间表示根据特征阈值来做分类，这样每一个弱分类器都类似于一个单节点的决策树，其实就是阈值判断而已，右边的三角形对每个弱分类器赋予一个权重，最后根据每个弱分类器的加权组合来判断总体类别。要注意一下数据集从上到下三个矩形内的直方图不一样，这表示每个样本的权重也发生了变化，样本权重的一开始初始化成相等的权重，然后根据弱分类器的错误率来调整每个弱分类器的全总alpha,如（图一）中的三角形所示，alpha 的计算如（公式一）所示：

（公式一）

        从（公式一）中也能感觉出来，弱分类器权重alpha和弱分类器分类错误率epsilon成反比，如果不能看出反比关系，分子分母同时除以epsilon就可以了，而ln是单调函数。这很make sense,当然分类器的错误率越高，越不能器重它，它的权重就应该低。同样的道理，样本也要区分对待，样本的权重要用弱分类器权重来计算，其实也是间接靠分类错误率，如（公式二）所示：

(公式二)

        其中D表示样本权重向量，有多少个样本就有多少个权重，下标i表示样本索引，而上标t表示上一次分类器训练迭代次数。这样一直更新迭代，一直到最大迭代次数或者整个分类器错误率为0或者不变时停止迭代，就完成了Adaboost的训练。但是这样就可以把样本分开了吗？下面从一组图解答这个问题，如（图二）所示：

（图二）

         由（图二）所示，每个弱分类器Hi可以要求不高的准确率，哪怕错误率是50%也可以接受，但是最后通过线性加权组合就可以得到一个很好的分类器，这点也可以通过错误率分析验证，有兴趣的可以看看：http://math.mit.edu/~rothvoss/18.304.3PM/Presentations/1-Eric-Boosting304FinalRpdf.pdf，想了解为什么alpha的计算如（公式一）的样子，可以看看：http://math.mit.edu/~rothvoss/18.304.3PM/Presentations/1-Eric-Boosting304FinalRpdf.pdf。

这样Adaboost的原理基本分析完毕，下面进入代码实战阶段：

首先来准备个简单数据集：

[python]  view plain copy
  1. from numpy import *  
  2.   
  3. def loadSimpData():        
  4.     datMat = matrix([[ 1. ,  2.1],  
  5.         [ 2. ,  1.1],  
  6.         [ 1.3,  1. ],  
  7.         [ 1. ,  1. ],  
  8.         [ 2. ,  1. ]])  
  9.     classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]  
  10.     return datMat,classLabels  

       上面有5个样本，接下来就是初始化每个样本的权重，刚开始相等的：

[python]  view plain copy
  1. D = mat(ones((5,1))/5)  

        有了样本和初始化权重，接下来的任务就是构建一个弱分类器，其实就是一个单节点决策树，找到决策树每个特征维度上对应的最佳阈值以及表示是大于阈值还是小于阈值为正样本的标识符。代码如下：

[python]  view plain copy
  1. def buildStump(dataArr,classLabels,D):  
  2.     dataMatrix = mat(dataArr); labelMat = mat(classLabels).T  
  3.     m,n = shape(dataMatrix)  
  4.     numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))  
  5.     minError = inf #init error sum, to +infinity  
  6.     for i in range(n):#loop over all dimensions  
  7.         rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();  
  8.         stepSize = (rangeMax-rangeMin)/numSteps  
  9.         for j in range(-1,int(numSteps)+1):#loop over all range in current dimension  
  10.             for inequal in ['lt', 'gt']: #go over less than and greater than  
  11.                 threshVal = (rangeMin + float(j) * stepSize)  
  12.                 predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan  
  13.                 errArr = mat(ones((m,1)))  
  14.                 errArr[predictedVals == labelMat] = 0  
  15.                 weightedError = D.T*errArr  #calc total error multiplied by D  
  16.                 #print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)  
  17.                 if weightedError < minError:  
  18.                     minError = weightedError  
  19.                     bestClasEst = predictedVals.copy()  
  20.                     bestStump['dim'] = i  
  21.                     bestStump['thresh'] = threshVal  
  22.                     bestStump['ineq'] = inequal  
  23.     return bestStump,minError,bestClasEst  

          注意代码中有三个for循环，这三个for循环其实就是为了完成决策树的每个特征维度上对应的最佳阈值以及表示是大于阈值还是小于阈值为正样本的标识符，这三个要素。其中it,gt分别表示大于和小于，阈值的选择是靠增加步长来需找，最终三者的确定是靠决策树分类错误率最小者决定，每个决策树的分类代码如下，很简单，就是靠阈值判断：

[python]  view plain copy
  1. def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data  
  2.     retArray = ones((shape(dataMatrix)[0],1))  
  3.     if threshIneq == 'lt':  
  4.         retArray[dataMatrix[:,dimen] <= threshVal] = -1.0  
  5.     else:  
  6.         retArray[dataMatrix[:,dimen] > threshVal] = -1.0  
  7.     return retArray  

        有了弱分类器的构造代码，下面来看Adaboost的训练代码：

[python]  view plain copy
  1. def adaBoostTrainDS(dataArr,classLabels,numIt=40):  
  2.     weakClassArr = []  
  3.     m = shape(dataArr)[0]  
  4.     D = mat(ones((m,1))/m)   #init D to all equal  
  5.     aggClassEst = mat(zeros((m,1)))  
  6.     for i in range(numIt):  
  7.         bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump  
  8.         #print "D:",D.T  
  9.         alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0  
  10.         bestStump['alpha'] = alpha    
  11.         weakClassArr.append(bestStump)                  #store Stump Params in Array  
  12.         #print "classEst: ",classEst.T  
  13.         expon = multiply(-1*alpha*mat(classLabels).T,classEst) #exponent for D calc, getting messy  
  14.         D = multiply(D,exp(expon))                              #Calc New D for next iteration  
  15.         D = D/D.sum()  
  16.         #calc training error of all classifiers, if this is 0 quit for loop early (use break)  
  17.         aggClassEst += alpha*classEst  
  18.         #print "aggClassEst: ",aggClassEst.T  
  19.         aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))  
  20.         errorRate = aggErrors.sum()/m  
  21.         print "total error: ",errorRate  
  22.         if errorRate == 0.0: break  
  23.     return weakClassArr,aggClassEst  

       上面的代码中训练过程主要任务就是完成（公式二）中的样本权重D和弱分类器权重alpha的更新，另外还要注意一下，代码中迭代了40次，每次都调用了buildStump，这就意味着创建了40个弱分类器。当模型收敛后，有了样本权重和弱弱弱分类器权重，最后就是对测试样本进行分类，分类代码如下：

[python]  view plain copy
  1. def adaClassify(datToClass,classifierArr):  
  2.     dataMatrix = mat(datToClass)#do stuff similar to last aggClassEst in adaBoostTrainDS  
  3.     m = shape(dataMatrix)[0]  
  4.     aggClassEst = mat(zeros((m,1)))  
  5.     for i in range(len(classifierArr)):  
  6.         classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\  
  7.                                  classifierArr[i]['thresh'],\  
  8.                                  classifierArr[i]['ineq'])#call stump classify  
  9.         aggClassEst += classifierArr[i]['alpha']*classEst  
  10.         print aggClassEst  
  11.     return sign(aggClassEst)  

     考虑到有些做学术的为了比较不同机器学习算法的好坏，常常需要画ROC曲线，这里也给出画ROC的代码：

[python]  view plain copy
  1. def plotROC(predStrengths, classLabels):  
  2.     import matplotlib.pyplot as plt  
  3.     cur = (1.0,1.0) #cursor  
  4.     ySum = 0.0 #variable to calculate AUC  
  5.     numPosClas = sum(array(classLabels)==1.0)  
  6.     yStep = 1/float(numPosClas); xStep = 1/float(len(classLabels)-numPosClas)  
  7.     sortedIndicies = predStrengths.argsort()#get sorted index, it's reverse  
  8.     fig = plt.figure()  
  9.     fig.clf()  
  10.     ax = plt.subplot(111)  
  11.     #loop through all the values, drawing a line segment at each point  
  12.     for index in sortedIndicies.tolist()[0]:  
  13.         if classLabels[index] == 1.0:  
  14.             delX = 0; delY = yStep;  
  15.         else:  
  16.             delX = xStep; delY = 0;  
  17.             ySum += cur[1]  
  18.         #draw line from cur to (cur[0]-delX,cur[1]-delY)  
  19.         ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b')  
  20.         cur = (cur[0]-delX,cur[1]-delY)  
  21.     ax.plot([0,1],[0,1],'b--')  
  22.     plt.xlabel('False positive rate'); plt.ylabel('True positive rate')  
  23.     plt.title('ROC curve for AdaBoost horse colic detection system')  
  24.     ax.axis([0,1,0,1])  
  25.     plt.show()  
  26.     print "the Area Under the Curve is: ",ySum*xStep  

       到此位置，Adaboost的代码也介绍完了，最终程序的运行结果如（图三）所示：

（图三）

       而Adaboost的模型ROC运行曲线如（图四）所示：


（图四）

最近MIT的几个人证明了Adaboost可以用一阶梯度的角度来解释，详见链接


参考文献：

[1] machinelearning in action.

[2] http://www.robots.ox.ac.uk/~az/lectures/cv/adaboost_matas.pdf

机器学习理论与实战（八）回归

  按照《机器学习实战》的主线，结束有监督学习中关于分类的机器学习方法，进入回归部分。所谓回归就是数据进行曲线拟合，回归一般用来做预测，涵盖线性回归（经典最小二乘法）、局部加权线性回归、岭回归和逐步线性回归。先来看下线性回归，即经典最小二乘法，说到最小二乘法就不得说下线性代数，因为一般说线性回归只通过计算一个公式就可以得到答案，如（公式一）所示：


（公式一）

       其中X是表示样本特征组成的矩阵，Y表示对应的值，比如房价，股票走势等，（公式一）是直接通过对（公式二）求导得到的，因为（公式二）是凸函数，导数等于零的点就是最小点。

（公式二）

         不过并不是所有的码农能从（公式二）求导得到（公式一）的解，因此这里给出另外一个直观的解，直观理解建立起来后，后续几个回归就简单类推咯。从初中的投影点说起，如（图一）所示：

（图一）

       在（图一）中直线a上离点b最近的点是点b在其上的投影，即垂直于a的交点p。p是b在a上的投影点。试想一下，如果我们把WX看成多维的a,即空间中的一个超面来代替二维空间中的直线，而y看成b,那现在要使得（公式二）最小是不是就是寻找（图一）中的e,即垂直于WX的垂线，因为只有垂直时e才最小。下面来看看如何通过寻找垂线并最终得到W。要寻找垂线，先从（图二）中的夹角theta 说起吧，因为当cos(theta)=0时，他们也就垂直了。下面来分析下直线或者向量之间的夹角，如（图二）所示：


（图二）

       在（图二）中， 表示三角形 的斜边，那么：

       角beta也可以得到同样的计算公式，接着利用三角形和差公式得到（公式三）：


（公式三）

        （公式三）表示的是两直线或者两向量之间的夹角公式，很多同学都学过。再仔细看下，发现分子其实是向量a,b之间的内积（点积），因此公式三变为简洁的（公式四）的样子：

（公式四）

接下来继续分析（图一）中的投影，为了方便观看，增加了一些提示如（图三）所示：

（图三）

        在（图三）中，假设向量b在向量a中的投影为p（注意，这里都上升为向量空间，不再使用直线，因为（公式四）是通用的）。投影p和a 在同一方向上（也可以反方向），因此我们可以用一个系数乘上a来表示p,比如（图三）中的 ，有了投影向量p，那么我们就可以表示向量e,因为根据向量法则， ，有因为a和e垂直，因此 ，展开求得系数x,如（公式五）所示：


（公式五）

（公式五）是不是很像（公式一）？只不过公式一的分母写成了另外的形式，不过别急，现在的系数只是一个标量数字，因为a,b都是一个向量，我们要扩展一下，把a从向量扩展到子空间，因为（公式一）中的X是样本矩阵，矩阵有列空间和行空间，如（图四）所示：

（图四）

        （图四）中的A表示样本矩阵X，假设它有两个列a1和a2,我们要找一些线性组合系数来找一个和（图三）一样的接受b 投影的向量，而这个向量通过矩阵列和系数的线性组合表示。求解的这个系数的思路和上面完全一样，就是寻找投影所在的向量和垂线e的垂直关系，得到系数，如（公式六）所示：

（公式六）

       这下（公式六）和（公式一）完全一样了，基于最小二乘法的线性回归也就推导完成了，而局部加权回归其实只是相当于对不同样本之间的关系给出了一个权重，所以叫局部加权，如（公式七）所示：

（公式七）

       而权重的计算可通过高斯核（高斯公式）来完成，核的作用就是做权重衰减，很多地方都要用到，表示样本的重要程度，一般离目标进的重要程度大些，高斯核可以很好的描述这种关系。如（公式八）所示，其中K是个超参数，根据情况灵活设置：

（公式八）

       （图五）是当K分别为1.0, 0.01,0.003时的局部加权线性回归的样子，可以看出当K=1.0时，和线性回归没区别：

（图五）

  而岭回归的样子如（公式九）所示：

（公式九）

        岭回归主要是解决的问题就是当XX’无法求逆时，比如当特征很多，样本很少，矩阵X不是满秩矩阵，此时求逆会出错，但是通过加上一个对角为常量lambda的矩阵，就可以很巧妙的避免这个计算问题，因此会多一个参数lambda,lambda的最优选择由交叉验证（cross-validation）来决定，加上一个对角不为0的矩阵很形象的在对角上抬高了，因此称为岭。不同的lambda会使得系数缩减，如（图六）所示：

（图六）

         说到系数缩减大家可能会觉得有奇怪，感觉有点类似于正则，但是这里只是相当于在（公式六）中增大分母，进而缩小系数，另外还有一些系数缩减的方法，比如直接增加一些约束，如（公式十）和（公式十一）所示：

（公式十）

（公式十一）

        当线性回归增加了（公式十）的约束变得和桥回归差不多，系数缩减了，而如果增加了（公式十一）的约束时就是稀疏回归咯，（我自己造的名词，sorry）,系数有一些0。

有了约束后，求解起来就不像上面那样直接计算个矩阵运算就行了，回顾第五节说中支持向量机原理，需要使用二次规划求解，不过仍然有一些像SMO算法一样的简化求解算法，比如前向逐步回归方法：

前向逐步回归的伪代码如（图七）所示，也不难，仔细阅读代码就可以理解：

（图七）

 

     下面直接给出上面四种回归的代码：

     

[python]  view plain copy
  1. from numpy import *  
  2.   
  3. def loadDataSet(fileName):      #general function to parse tab -delimited floats  
  4.     numFeat = len(open(fileName).readline().split('\t')) - 1 #get number of fields   
  5.     dataMat = []; labelMat = []  
  6.     fr = open(fileName)  
  7.     for line in fr.readlines():  
  8.         lineArr =[]  
  9.         curLine = line.strip().split('\t')  
  10.         for i in range(numFeat):  
  11.             lineArr.append(float(curLine[i]))  
  12.         dataMat.append(lineArr)  
  13.         labelMat.append(float(curLine[-1]))  
  14.     return dataMat,labelMat  
  15.   
  16. def standRegres(xArr,yArr):  
  17.     xMat = mat(xArr); yMat = mat(yArr).T  
  18.     xTx = xMat.T*xMat  
  19.     if linalg.det(xTx) == 0.0:  
  20.         print "This matrix is singular, cannot do inverse"  
  21.         return  
  22.     ws = xTx.I * (xMat.T*yMat)  
  23.     return ws  
  24.   
  25. def lwlr(testPoint,xArr,yArr,k=1.0):  
  26.     xMat = mat(xArr); yMat = mat(yArr).T  
  27.     m = shape(xMat)[0]  
  28.     weights = mat(eye((m)))  
  29.     for j in range(m):                      #next 2 lines create weights matrix  
  30.         diffMat = testPoint - xMat[j,:]     #  
  31.         weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))  
  32.     xTx = xMat.T * (weights * xMat)  
  33.     if linalg.det(xTx) == 0.0:  
  34.         print "This matrix is singular, cannot do inverse"  
  35.         return  
  36.     ws = xTx.I * (xMat.T * (weights * yMat))  
  37.     return testPoint * ws  
  38.   
  39. def lwlrTest(testArr,xArr,yArr,k=1.0):  #loops over all the data points and applies lwlr to each one  
  40.     m = shape(testArr)[0]  
  41.     yHat = zeros(m)  
  42.     for i in range(m):  
  43.         yHat[i] = lwlr(testArr[i],xArr,yArr,k)  
  44.     return yHat  
  45.   
  46. def lwlrTestPlot(xArr,yArr,k=1.0):  #same thing as lwlrTest except it sorts X first  
  47.     yHat = zeros(shape(yArr))       #easier for plotting  
  48.     xCopy = mat(xArr)  
  49.     xCopy.sort(0)  
  50.     for i in range(shape(xArr)[0]):  
  51.         yHat[i] = lwlr(xCopy[i],xArr,yArr,k)  
  52.     return yHat,xCopy  
  53.   
  54. def rssError(yArr,yHatArr): #yArr and yHatArr both need to be arrays  
  55.     return ((yArr-yHatArr)**2).sum()  
  56.   
  57. def ridgeRegres(xMat,yMat,lam=0.2):  
  58.     xTx = xMat.T*xMat  
  59.     denom = xTx + eye(shape(xMat)[1])*lam  
  60.     if linalg.det(denom) == 0.0:  
  61.         print "This matrix is singular, cannot do inverse"  
  62.         return  
  63.     ws = denom.I * (xMat.T*yMat)  
  64.     return ws  
  65.       
  66. def ridgeTest(xArr,yArr):  
  67.     xMat = mat(xArr); yMat=mat(yArr).T  
  68.     yMean = mean(yMat,0)  
  69.     yMat = yMat - yMean     #to eliminate X0 take mean off of Y  
  70.     #regularize X's  
  71.     xMeans = mean(xMat,0)   #calc mean then subtract it off  
  72.     xVar = var(xMat,0)      #calc variance of Xi then divide by it  
  73.     xMat = (xMat - xMeans)/xVar  
  74.     numTestPts = 30  
  75.     wMat = zeros((numTestPts,shape(xMat)[1]))  
  76.     for i in range(numTestPts):  
  77.         ws = ridgeRegres(xMat,yMat,exp(i-10))  
  78.         wMat[i,:]=ws.T  
  79.     return wMat  
  80.   
  81. def regularize(xMat):#regularize by columns  
  82.     inMat = xMat.copy()  
  83.     inMeans = mean(inMat,0)   #calc mean then subtract it off  
  84.     inVar = var(inMat,0)      #calc variance of Xi then divide by it  
  85.     inMat = (inMat - inMeans)/inVar  
  86.     return inMat  
  87.   
  88. def stageWise(xArr,yArr,eps=0.01,numIt=100):  
  89.     xMat = mat(xArr); yMat=mat(yArr).T  
  90.     yMean = mean(yMat,0)  
  91.     yMat = yMat - yMean     #can also regularize ys but will get smaller coef  
  92.     xMat = regularize(xMat)  
  93.     m,n=shape(xMat)  
  94.     #returnMat = zeros((numIt,n)) #testing code remove  
  95.     ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()  
  96.     for i in range(numIt):  
  97.         print ws.T  
  98.         lowestError = inf;   
  99.         for j in range(n):  
  100.             for sign in [-1,1]:  
  101.                 wsTest = ws.copy()  
  102.                 wsTest[j] += eps*sign  
  103.                 yTest = xMat*wsTest  
  104.                 rssE = rssError(yMat.A,yTest.A)  
  105.                 if rssE < lowestError:  
  106.                     lowestError = rssE  
  107.                     wsMax = wsTest  
  108.         ws = wsMax.copy()  
  109.         #returnMat[i,:]=ws.T  
  110.     #return returnMat  
  111.   
  112. #def scrapePage(inFile,outFile,yr,numPce,origPrc):  
  113. #    from BeautifulSoup import BeautifulSoup  
  114. #    fr = open(inFile); fw=open(outFile,'a') #a is append mode writing  
  115. #    soup = BeautifulSoup(fr.read())  
  116. #    i=1  
  117. #    currentRow = soup.findAll('table', r="%d" % i)  
  118. #    while(len(currentRow)!=0):  
  119. #        title = currentRow[0].findAll('a')[1].text  
  120. #        lwrTitle = title.lower()  
  121. #        if (lwrTitle.find('new') > -1) or (lwrTitle.find('nisb') > -1):  
  122. #            newFlag = 1.0  
  123. #        else:  
  124. #            newFlag = 0.0  
  125. #        soldUnicde = currentRow[0].findAll('td')[3].findAll('span')  
  126. #        if len(soldUnicde)==0:  
  127. #            print "item #%d did not sell" % i  
  128. #        else:  
  129. #            soldPrice = currentRow[0].findAll('td')[4]  
  130. #            priceStr = soldPrice.text  
  131. #            priceStr = priceStr.replace('$','') #strips out $  
  132. #            priceStr = priceStr.replace(',','') #strips out ,  
  133. #            if len(soldPrice)>1:  
  134. #                priceStr = priceStr.replace('Free shipping', '') #strips out Free Shipping  
  135. #            print "%s\t%d\t%s" % (priceStr,newFlag,title)  
  136. #            fw.write("%d\t%d\t%d\t%f\t%s\n" % (yr,numPce,newFlag,origPrc,priceStr))  
  137. #        i += 1  
  138. #        currentRow = soup.findAll('table', r="%d" % i)  
  139. #    fw.close()  
  140.       
  141. from time import sleep  
  142. import json  
  143. import urllib2  
  144. def searchForSet(retX, retY, setNum, yr, numPce, origPrc):  
  145.     sleep(10)  
  146.     myAPIstr = 'AIzaSyD2cR2KFyx12hXu6PFU-wrWot3NXvko8vY'  
  147.     searchURL = 'https://www.googleapis.com/shopping/search/v1/public/products?key=%s&country=US&q=lego+%d&alt=json' % (myAPIstr, setNum)  
  148.     pg = urllib2.urlopen(searchURL)  
  149.     retDict = json.loads(pg.read())  
  150.     for i in range(len(retDict['items'])):  
  151.         try:  
  152.             currItem = retDict['items'][i]  
  153.             if currItem['product']['condition'] == 'new':  
  154.                 newFlag = 1  
  155.             else: newFlag = 0  
  156.             listOfInv = currItem['product']['inventories']  
  157.             for item in listOfInv:  
  158.                 sellingPrice = item['price']  
  159.                 if  sellingPrice > origPrc * 0.5:  
  160.                     print "%d\t%d\t%d\t%f\t%f" % (yr,numPce,newFlag,origPrc, sellingPrice)  
  161.                     retX.append([yr, numPce, newFlag, origPrc])  
  162.                     retY.append(sellingPrice)  
  163.         except: print 'problem with item %d' % i  
  164.       
  165. def setDataCollect(retX, retY):  
  166.     searchForSet(retX, retY, 8288, 2006, 800, 49.99)  
  167.     searchForSet(retX, retY, 10030, 2002, 3096, 269.99)  
  168.     searchForSet(retX, retY, 10179, 2007, 5195, 499.99)  
  169.     searchForSet(retX, retY, 10181, 2007, 3428, 199.99)  
  170.     searchForSet(retX, retY, 10189, 2008, 5922, 299.99)  
  171.     searchForSet(retX, retY, 10196, 2009, 3263, 249.99)  
  172.       
  173. def crossValidation(xArr,yArr,numVal=10):  
  174.     m = len(yArr)                             
  175.     indexList = range(m)  
  176.     errorMat = zeros((numVal,30))#create error mat 30columns numVal rows  
  177.     for i in range(numVal):  
  178.         trainX=[]; trainY=[]  
  179.         testX = []; testY = []  
  180.         random.shuffle(indexList)  
  181.         for j in range(m):#create training set based on first 90% of values in indexList  
  182.             if j < m*0.9:   
  183.                 trainX.append(xArr[indexList[j]])  
  184.                 trainY.append(yArr[indexList[j]])  
  185.             else:  
  186.                 testX.append(xArr[indexList[j]])  
  187.                 testY.append(yArr[indexList[j]])  
  188.         wMat = ridgeTest(trainX,trainY)    #get 30 weight vectors from ridge  
  189.         for k in range(30):#loop over all of the ridge estimates  
  190.             matTestX = mat(testX); matTrainX=mat(trainX)  
  191.             meanTrain = mean(matTrainX,0)  
  192.             varTrain = var(matTrainX,0)  
  193.             matTestX = (matTestX-meanTrain)/varTrain #regularize test with training params  
  194.             yEst = matTestX * mat(wMat[k,:]).T + mean(trainY)#test ridge results and store  
  195.             errorMat[i,k]=rssError(yEst.T.A,array(testY))  
  196.             #print errorMat[i,k]  
  197.     meanErrors = mean(errorMat,0)#calc avg performance of the different ridge weight vectors  
  198.     minMean = float(min(meanErrors))  
  199.     bestWeights = wMat[nonzero(meanErrors==minMean)]  
  200.     #can unregularize to get model  
  201.     #when we regularized we wrote Xreg = (x-meanX)/var(x)  
  202.     #we can now write in terms of x not Xreg:  x*w/var(x) - meanX/var(x) +meanY  
  203.     xMat = mat(xArr); yMat=mat(yArr).T  
  204.     meanX = mean(xMat,0); varX = var(xMat,0)  
  205.     unReg = bestWeights/varX  
  206.     print "the best model from Ridge Regression is:\n",unReg  
  207.     print "with constant term: ",-1*sum(multiply(meanX,unReg)) + mean(yMat)  


以上各种回归方法没有考虑实际数据的噪声，如果噪声很多，直接用上述的回归不是太好，因此需要加上正则，然后迭代更新权重

参考文献：

         [1] machine learning in action.Peter Harrington 

       [2]Linear Algebra and Its Applications_4ed.Gilbert_Strang

机器学习理论与实战（九）回归树和模型树

  前一节的回归是一种全局回归模型，它设定了一个模型，不管是线性还是非线性的模型，然后拟合数据得到参数，现实中会有些数据很复杂，肉眼几乎看不出符合那种模型，因此构建全局的模型就有点不合适。这节介绍的树回归就是为了解决这类问题，它通过构建决策节点把数据数据切分成区域，然后局部区域进行回归拟合。先来看看分类回归树吧（CART:Classification And Regression Trees）,这个模型优点就是上面所说，可以对复杂和非线性的数据进行建模，缺点是得到的结果不容易理解。顾名思义它可以做分类也可以做回归，至于分类前面在说决策树时已经说过了，这里略过。直接通过分析回归树的代码来理解吧：

[python]  view plain copy
  1. from numpy import *  
  2.   
  3. def loadDataSet(fileName):      #general function to parse tab -delimited floats  
  4.     dataMat = []                #assume last column is target value  
  5.     fr = open(fileName)  
  6.     for line in fr.readlines():  
  7.         curLine = line.strip().split('\t')  
  8.         fltLine = map(float,curLine) #map all elements to float()  
  9.         dataMat.append(fltLine)  
  10.     return dataMat  
  11.   
  12. def binSplitDataSet(dataSet, feature, value):  
  13.     mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0],:][0]  
  14.     mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:][0]  
  15.     return mat0,mat1  

上面两个函数，第一个函数加载样本数据，第二个函数用来指定在某个特征和维度上切分数据，示例如（图一）所示：

机器学习理论与实战_第19张图片

机器学习理论与实战_第20张图片

（图一）

       注意一下，CART是一种通过二元切分来构建树的，前面的决策树的构建是通过香农熵最小作为度量，树的节点是个离散的阈值；这里不再使用香农熵，因为我们要做回归，因此这里使用计算分割数据的方差作为度量，而树的节点也对应使用使得方差最小的某个连续数值(其实是特征值)。试想一下，如果方差越小，说明误差那个节点最能表述那块数据。下面来看看树的构建代码：

[python]  view plain copy
  1. def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):#assume dataSet is NumPy Mat so we can array filtering  
  2.     feat, val = chooseBestSplit(dataSet, leafType, errType, ops)#choose the best split  
  3.     if feat == None: return val #if the splitting hit a stop condition return val(叶子节点值)  
  4.     retTree = {}  
  5.     retTree['spInd'] = feat  
  6.     retTree['spVal'] = val  
  7.     lSet, rSet = binSplitDataSet(dataSet, feat, val)  
  8.     retTree['left'] = createTree(lSet, leafType, errType, ops)  
  9.     retTree['right'] = createTree(rSet, leafType, errType, ops)  
  10.     return retTree    

         这段代码中主要工作任务就是选择最佳分割特征，然后分割，是叶子节点就返回，不是叶子节点就递归的生成树结构。其中调用了最佳分割特征的函数：chooseBestSplit，前面决策树的构建中，这个函数里用熵来度量，这里采用误差（方差）来度量，同样先看代码：

[python]  view plain copy
  1. def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):  
  2.     tolS = ops[0]; tolN = ops[1]  
  3.     #if all the target variables are the same value: quit and return value  
  4.     if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #exit cond 1  
  5.         return None, leafType(dataSet)  
  6.     m,n = shape(dataSet)  
  7.     #the choice of the best feature is driven by Reduction in RSS error from mean  
  8.     S = errType(dataSet)  
  9.     bestS = inf; bestIndex = 0; bestValue = 0  
  10.     for featIndex in range(n-1):  
  11.         for splitVal in set(dataSet[:,featIndex]):  
  12.             mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)  
  13.             if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): continue  
  14.             newS = errType(mat0) + errType(mat1)  
  15.             if newS < bestS:   
  16.                 bestIndex = featIndex  
  17.                 bestValue = splitVal  
  18.                 bestS = newS  
  19.     #if the decrease (S-bestS) is less than a threshold don't do the split  
  20.     if (S - bestS) < tolS:   
  21.         return None, leafType(dataSet) #exit cond 2  
  22.     mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)  
  23.     if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN):  #exit cond 3  
  24.         return None, leafType(dataSet)  
  25.     return bestIndex,bestValue#returns the best feature to split on  
  26.                               #and the value used for that split  

这段代码的主干是：

遍历每个特征：

       遍历每个特征值：

               把数据集切分成两份

               计算此时的切分误差

               如果切分误差小于当前最小误差，更新最小误差值，当前切分为最佳切分

返回最佳切分的特征值和阈值

 

       尤其注意最后的返回值，因为它是构建树每个节点成分的东西。另外代码中errType=regErr 调用了regErr函数来计算方差，下面给出：

               
[python]  view plain copy
  1. def regErr(dataSet):  
  2.     return var(dataSet[:,-1]) * shape(dataSet)[0]  

       如果误差变化不大时（代码中(S - bestS)），则生成叶子节点，叶子节点函数是：

[python]  view plain copy
  1. def regLeaf(dataSet):#returns the value used for each leaf  
  2.     return mean(dataSet[:,-1])  

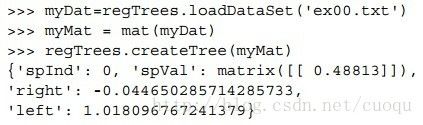
这样回归树构建的代码就初步分析完毕了，运行结果如（图二）所示：

机器学习理论与实战_第21张图片

（图二）

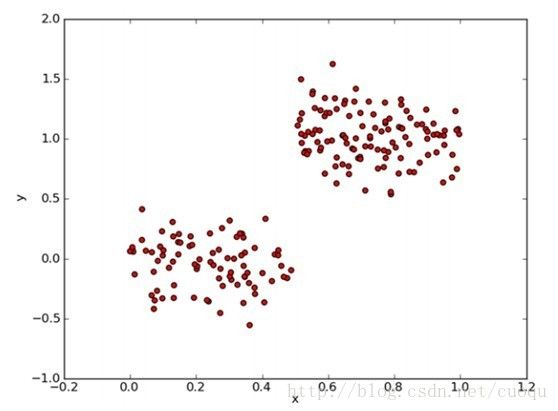
         数据ex00.txt在文章最后给出，它的分布如（图三）所示：

机器学习理论与实战_第22张图片

（图三）

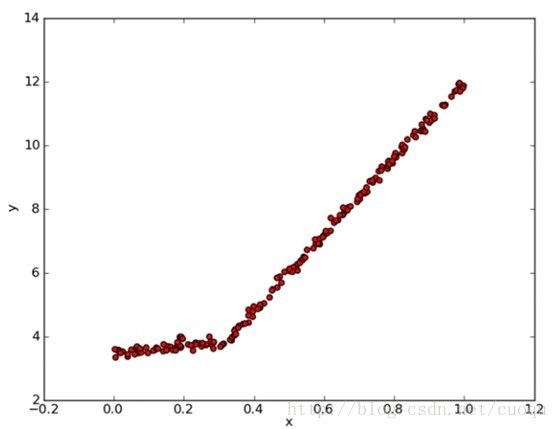
       根据（图三），我们可以大概看出（图二）的代码的运行结果具有一定的合理性，选用X（用0表示）特征作为分割特征，然后左右节点各选了一个中心值来描述树回归。节点比较少，但很能说明问题，下面给出一个比较复杂数据跑出的结果，如（图四）所示：

机器学习理论与实战_第23张图片

（图四）

对应的数据如（图五）所示：


机器学习理论与实战_第24张图片

（图五）

            对于树的叶子节点和节点值的合理性，大家逐个对照（图五）来验证吧。下面简单的说下树的修剪，如果特征维度比较高，很容易发生节点过多，造成过拟合，过拟合（overfit）会出现high variance, 而欠拟合(under fit)会出现high bias,这点是题外话，因为机器学习理论一般要讲这些，当出现过拟合时，一般使用正则方法，由于回归树没有建立目标函数，因此这里解决过拟合的方法就是修剪树，简单的说就是使用少量的、关键的特征来判别，下面来看看如何修剪树：很简单，就是递归的遍历一个子树，从叶子节点开始，计算同一父节点的两个子节点合并后的误差，再计算不合并的误差，如果合并会降低误差，就把叶子节点合并。说到误差，其实前面的chooseBestSplit函数里有一句代码：

[python]  view plain copy
  1. #if the decrease (S-bestS) is less than a threshold don't do the split  
  2.    if (S - bestS) < tolS:   

         tolS 是个阈值，当误差变化不太大时，就不再分裂下去，其实也是修剪树的方法，只不过它是事前修剪，而计算合并误差的则是事后修剪。下面是其代码：

[python]  view plain copy
  1. def getMean(tree):  
  2.     if isTree(tree['right']): tree['right'] = getMean(tree['right'])  
  3.     if isTree(tree['left']): tree['left'] = getMean(tree['left'])  
  4.     return (tree['left']+tree['right'])/2.0  
  5.       
  6. def prune(tree, testData):  
  7.     if shape(testData)[0] == 0: return getMean(tree) #if we have no test data collapse the tree  
  8.     if (isTree(tree['right']) or isTree(tree['left'])):#if the branches are not trees try to prune them  
  9.         lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])  
  10.     if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)  
  11.     if isTree(tree['right']): tree['right'] =  prune(tree['right'], rSet)  
  12.     #if they are now both leafs, see if we can merge them  
  13.     if not isTree(tree['left']) and not isTree(tree['right']):  
  14.         lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])  
  15.         errorNoMerge = sum(power(lSet[:,-1] - tree['left'],2)) +\  
  16.             sum(power(rSet[:,-1] - tree['right'],2))  
  17.         treeMean = (tree['left']+tree['right'])/2.0  
  18.         errorMerge = sum(power(testData[:,-1] - treeMean,2))  
  19.         if errorMerge < errorNoMerge:   
  20.             print "merging"  
  21.             return treeMean  
  22.         else: return tree  
  23.     else: return tree  

        说完了树回归，再简单的提下模型树，因为树回归每个节点是一些特征和特征值，选取的原则是根据特征方差最小。如果把叶子节点换成分段线性函数，那么就变成了模型树，如（图六）所示：

机器学习理论与实战_第25张图片

（图六）

      （图六）中明显是两个直线组成，以X坐标（0.0-0.3）和（0.3-1.0）分成的两个线段。如果我们用两个叶子节点保存两个线性回归模型，就完成了这部分数据的拟合。实现也比较简单，代码如下：

[python]  view plain copy
  1. def linearSolve(dataSet):   #helper function used in two places  
  2.     m,n = shape(dataSet)  
  3.     X = mat(ones((m,n))); Y = mat(ones((m,1)))#create a copy of data with 1 in 0th postion  
  4.     X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1]#and strip out Y  
  5.     xTx = X.T*X  
  6.     if linalg.det(xTx) == 0.0:  
  7.         raise NameError('This matrix is singular, cannot do inverse,\n\  
  8.         try increasing the second value of ops')  
  9.     ws = xTx.I * (X.T * Y)  
  10.     return ws,X,Y  
  11.   
  12. def modelLeaf(dataSet):#create linear model and return coeficients  
  13.     ws,X,Y = linearSolve(dataSet)  
  14.     return ws  
  15.   
  16. def modelErr(dataSet):  
  17.     ws,X,Y = linearSolve(dataSet)  
  18.     yHat = X * ws  
  19.     return sum(power(Y - yHat,2))  

       代码和树回归相似，只不过modelLeaf在返回叶子节点时，要完成一个线性回归，由linearSolve来完成。最后一个函数modelErr则和回归树的regErr函数起着同样的作用。

谢天谢地，这篇文章一个公式都没有出现，但同时也希望没有数学的语言，表述会清楚。


数据ex00.txt：

0.036098 0.155096

0.993349 1.077553

0.530897 0.893462

0.712386 0.564858

0.343554 -0.371700

0.098016 -0.332760

0.691115 0.834391

0.091358 0.099935

0.727098 1.000567

0.951949 0.945255

0.768596 0.760219

0.541314 0.893748

0.146366 0.034283

0.673195 0.915077

0.183510 0.184843

0.339563 0.206783

0.517921 1.493586

0.703755 1.101678

0.008307 0.069976

0.243909 -0.029467

0.306964 -0.177321

0.036492 0.408155

0.295511 0.002882

0.837522 1.229373

0.202054 -0.087744

0.919384 1.029889

0.377201 -0.243550

0.814825 1.095206

0.611270 0.982036

0.072243 -0.420983

0.410230 0.331722

0.869077 1.114825

0.620599 1.334421

0.101149 0.068834

0.820802 1.325907

0.520044 0.961983

0.488130 -0.097791

0.819823 0.835264

0.975022 0.673579

0.953112 1.064690

0.475976 -0.163707

0.273147 -0.455219

0.804586 0.924033

你可能感兴趣的:(Machine,Learning)

  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 简单了解 JVM 记得开心一点啊 jvm
    目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称，意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统（如：JVM、VMwave、VirtualBox）。JVM和其他两个虚拟机
  • JVM、JRE和 JDK：理解Java开发的三大核心组件 Y雨何时停T Javajava
    Java是一门跨平台的编程语言，它的成功离不开背后强大的运行环境与开发工具的支持。在Java的生态中，JVM（Java虚拟机）、JRE（Java运行时环境）和JDK（Java开发工具包）是三个至关重要的核心组件。本文将探讨JVM、JDK和JRE的区别，帮助你更好地理解Java的运行机制。1.JVM：Java虚拟机（JavaVirtualMachine）什么是JVM？JVM，即Java虚拟机，是Ja
  • 深度 Qlearning：在直播推荐系统中的应用 AGI通用人工智能之禅 程序员提升自我硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLMJavaPython架构设计Agent程序员实现财富自由
    深度Q-learning：在直播推荐系统中的应用关键词：深度Q-learning,强化学习,直播推荐系统,个性化推荐1.背景介绍1.1问题的由来随着互联网技术的飞速发展,直播平台如雨后春笋般涌现。面对海量的直播内容,用户很难快速找到自己感兴趣的内容。因此,个性化推荐系统在直播平台中扮演着越来越重要的角色。1.2研究现状目前,主流的个性化推荐算法包括协同过滤、基于内容的推荐等。这些方法在一定程度上缓
  • 管理员权限的软件不能开机自启动的解决方法 ss_ctrl
    这是几种解决方法：1.将启动参数写入到32位注册表里面去在64位系统下我们64位的程序访问此HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Run注册表路径，是可以正确访问的，32位程序访问此注册表路径时，默认会被系统自动映射到HKEY_LOCAL_MACHINE\SOFTWARE\WOW6432Node\Microsoft
  • golang学习笔记--MPG模型 xxzed golang#学习笔记学习笔记golang
    MPG模式：M（Machine）：操作系统的主线程P（Processor）：协程执行需要的资源（上下文context），可以看作一个局部的调度器，使go代码在一个线程上跑，他是实现从N：1到N：M映射的关键G（Goroutine）：协程，有自己的栈。包含指令指针（instructionpointer）和其它信息（正在等待的channel等等），用于调度。一个P下面可以有多个G1、当前程序有三个M,
  • 【开发环境搭建】Macbook M1搭建Java开发环境 weixin_44329069 java开发语言
    JDK安装与配置下载并安装JDK：ARM64DMG安装包下载链接：JDK21forMac(ARM64)。双击下载的DMG文件，按照提示安装JDK。配置环境变量：打开终端，使用vim编辑.bash_profile文件：vim~/.bash_profile在文件中添加以下内容来设置JAVA_HOME：exportJAVA_HOME=/Library/Java/JavaVirtualMachines/j
  • 云服务业界动态简报-20180128 Captain7
    一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud，包含了主流的深度学习框架及数据科学工具包，通过QingCloudAppCenter一键部署交付，可以让算法工程师和数据科学家快速构建深度学习开发环境，将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵，涵盖企业版、大数据版、AI
  • 机器学习VS深度学习 nfgo 机器学习
    机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
  • ResNet的半监督和半弱监督模型 Valar_Morghulis
    Billion-scalesemi-supervisedlearningforimageclassificationhttps://arxiv.org/pdf/1905.00546.pdfhttps://github.com/facebookresearch/semi-supervised-ImageNet1K-models/权重在timm中也有：https://hub.fastgit.org/r
  • 联邦学习 Federated learning Google I/O‘19 笔记 努力搬砖的星期五 笔记联邦学习机器学习机器学习tensorflow
    FederatedLearning:MachineLearningonDecentralizeddatahttps://www.youtube.com/watch?v=89BGjQYA0uE文章目录FederatedLearning:MachineLearningonDecentralizeddata1.DecentralizeddataEdgedevicesGboard:mobilekeyboa
  • PCL 怎样可视化深度图像 LeonDL168 PCL计算机视觉人工智能视觉检测图像处理算法
    本小节讲解如何可视化深度图像的两种方法，在3D视窗中以点云形式进行可视化（深度图像来源于点云），另一种是，将深度值映射为颜色，从而以彩色图像方式可视化深度图像。代码首先，在PCL（PointCloudLearning）中国协助发行的书提供光盘的第7章例2文件夹中，打开名为range_image_visualization.cpp的代码文件，同文件夹下可以找到相关的测试点云文件room_scan1.
  • FISCO BCOS（十七）——— go SDK的使用 林中有神君 #FISCOBCOS2.8.0golang服务器linuxfiscobcos区块链
    1、创建一个工作目录root@wyg-virtual-machine:~/fisco#mkdirgoWorkSpace2、下载go-sdkroot@wyg-virtual-machine:~/fisco/
  • Git报错（一）fatal: Could not read from remote repository. librarycode
    解决方案来自CSDN：https://blog.csdn.net/cxwtsh123/article/details/79194263?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.control&dist_request_id=&depth_1-utm_source=distr
  • VOC数据集转换为CoCo数据集（亲测有效） 情书学长 人工智能学习笔记图像处理
    #VOC数据集格式VOC格式的数据集分为3部分，Annotations、ImageSets、JPEGImages。（一）Annotations：存放数据标注的xml文件，格式如下：CUMID_train0001.pngC:\Users\86182\Desktop\CUMID_train\0001.pngUnknown2040136830MachineUnspecified0011933491451
  • 【Vesta发号器源码】PropertyMachineIdsProvider DeanChangDM
    Vesta发号器源码解析——PropertyMachineIdsProvider属性配置文件持有Id的模式,没啥东西，比单个的多了一个获取下一个的方法封装实现上略有一点点区别privatelong[]machineIds;privateintcurrentIndex;publiclonggetNextMachineId(){returngetMachineId();}publiclonggetMa
  • Awesome TensorFlow weixin_30594001 人工智能移动开发大数据
    AwesomeTensorFlowAcuratedlistofawesomeTensorFlowexperiments,libraries,andprojects.Inspiredbyawesome-machine-learning.WhatisTensorFlow?TensorFlowisanopensourcesoftwarelibraryfornumericalcomputationusin
  • 【ShuQiHere】探索人工智能核心：机器学习的奥秘 ShuQiHere 人工智能机器学习
    【ShuQiHere】什么是机器学习？机器学习（MachineLearning,ML）是人工智能（ArtificialIntelligence,AI）中最关键的组成部分之一。它使得计算机不仅能够处理数据，还能从数据中学习，从而做出预测和决策。无论是语音识别、自动驾驶还是推荐系统，背后都依赖于机器学习模型。机器学习与传统的编程不同，它不再依赖于人类编写的固定规则，而是通过数据自我改进模型，从而更灵活
  • 综述论文“A Survey of Zero-Shot Learning: Settings, Methods, and Applications” 硅谷秋水 机器学习机器学习神经网络深度学习
    该零样本学习综述，发表于ACMTrans.Intell.Syst.Technol.10,2,Article13(January2019)摘要：大多数机器学习方法着重于对已经在训练中看到其类别的实例进行分类。实际上，许多应用程序需要对实例进行分类，而这些实例的类以前没有见过。零样本学习（Zero-ShotLearning）是一种强大而有前途的学习范例，其中训练实例涵盖的类别与想分类的类别是不相交的。
  • go-etcd实战 小书go golang实战演练golangetcd服务发现服务注册微服务
    etcd简介etcdisastronglyconsistent,distributedkey-valuestorethatprovidesareliablewaytostoredatathatneedstobeaccessedbyadistributedsystemorclusterofmachines.Itgracefullyhandlesleaderelectionsduringnetwork
  • 梯度提升机 (Gradient Boosting Machines, GBM) ALGORITHM LOL boosting集成学习机器学习
    梯度提升机(GradientBoostingMachines,GBM)通俗易懂算法梯度提升机（GradientBoostingMachines，GBM）是一种集成学习算法，主要用于回归和分类问题。GBM本质上是通过训练一系列简单的模型（通常是决策树），然后将这些模型组合起来，从而提高整体预测性能。基本步骤初始模型：首先，我们用一个简单的模型（如一个常数值）作为预测模型，记为F0(x)F_0(x)F
  • 机器学习 VS 表示学习 VS 深度学习 Efred.D 人工智能机器学习深度学习人工智能
    文章目录前言一、机器学习是什么?二、表示学习三、深度学习总结前言本文主要阐述机器学习,表示学习和深度学习的原理和区别.一、机器学习是什么?机器学习(machinelearning),是从有限的数据集中学习到一定的规律,再把学到的规律应用到一些相似的样本集中做预测.机器学习的历史可以追溯到20世纪40年代McCulloch提出的人工神经元网络,目前学界大致把机器学习分为传统机器学习和机器学习两个类别
  • 端到端的自动驾驶论文与代码整理 大别山伧父 自动驾驶
    LearningbyCheatinggithubcodearxivpaperconferenceonrobotlearning最新进展(May2021)Checkoutourlatestfollow-upwork:WorldonRails(2020)Checkoutoursubmissiontothe2020CARLAChallenge!pass
  • JVM 架构 : 运行时数据区 & 内存结构 光剑书架上的书
    JVM:JavaVirtualMachine架构JVMArchitectureRuntimeDataArea/MemoryStructureClassloaderClassloaderisasubsysteminJVM,whichisprimarilyresponasibleforloadingthejavaclasses,thereare3differentclassloaders:Bootst
  • Lt-8 Multithreading yanlingyun0210 java
    IntendedLearningOutcomesTounderstandtheconceptofconcurrency.Tounderstandthedifferenceofaprocessandathread.TodefineathreadusingtheThreadclassandRunnableinterface.TocontrolthreadswithvariousThreadmethod
  • 如何使用Pytorch-Metric-Learning？ 鱼儿也有烦恼 PyTorchpytorch
    文章目录如何使用Pytorch-Metric-Learning？1.Pytorch-Metric-Learning库9个模块的功能1.1Sampler模块1.2Miner模块1.3Loss模块1.4Reducer模块1.5Distance模块1.6Regularizer模块1.7Trainer模块1.8Tester模块1.9Utils模块2.如何使用PyTorchMetricLearning库中的
  • risc-v特权模式 狮子座硅农（Leo ICer） risc-v
    risc-v架构定义了3种工作模式，又称为特权模式（privilegedmode）。机器模式（machinemode），简称M模式；监督模式（supervisormode），简称S模式；用户模式（usermode），简称U模式。risc-v架构定义机器模式为必选模式，另外两种模式为可选模式，通过不同的模式组合可以实现不同的系统。risc-v架构支持几种不同的存储器地址管理机制，包括对物理地址和虚拟
  • 推荐开源项目：PyTorch-Metric-Learning 潘惟妍
    推荐开源项目：PyTorch-Metric-Learningpytorch-metric-learningTheeasiestwaytousedeepmetriclearninginyourapplication.Modular,flexible,andextensible.WritteninPyTorch.项目地址:https://gitcode.com/gh_mirrors/py/pytorc
  • 推荐：FastAPI驱动的稳定扩散LLMs演示项目 褚知茉Jade
    推荐：FastAPI驱动的稳定扩散LLMs演示项目FastAPI-for-Machine-Learning-Live-DemoThisrepositorycontainsthefilestobuildyourveryownAIimagegenerationwebapplication!OutlinedarethecorecomponentsoftheFastAPIwebframework,anda
  • 【python】【Ray的概述】 资源存储库 python开发语言
    Overview概述Rayisanopen-sourceunifiedframeworkforscalingAIandPythonapplicationslikemachinelearning.Itprovidesthecomputelayerforparallelprocessingsothatyoudon’tneedtobeadistributedsystemsexpert.Rayminimi
  • iOS http封装 374016526 ios服务器交互http网络请求
    程序开发避免不了与服务器的交互，这里打包了一个自己写的http交互库。希望可以帮到大家。   内置一个basehttp，当我们创建自己的service可以继承实现。   KuroAppBaseHttp *baseHttp = [[KuroAppBaseHttp alloc] init]; [baseHttp setDelegate:self]; [baseHttp
  • lolcat ：一个在 Linux 终端中输出彩虹特效的命令行工具 brotherlamp linuxlinux教程linux视频linux自学linux资料
      那些相信 Linux 命令行是单调无聊且没有任何乐趣的人们，你们错了，这里有一些有关 Linux 的文章，它们展示着 Linux 是如何的有趣和“淘气” 。 在本文中，我将讨论一个名为“lolcat”的小工具 – 它可以在终端中生成彩虹般的颜色。 何为 lolcat ? Lolcat 是一个针对 Linux，BSD 和 OSX 平台的工具，它类似于 cat 命令，并为 cat
  • MongoDB索引管理（1）——[九] eksliang mongodbMongoDB管理索引
    转载请出自出处：http://eksliang.iteye.com/blog/2178427 一、概述       数据库的索引与书籍的索引类似，有了索引就不需要翻转整本书。数据库的索引跟这个原理一样，首先在索引中找，在索引中找到条目以后，就可以直接跳转到目标文档的位置，从而使查询速度提高几个数据量级。       不使用索引的查询称
  • Informatica参数及变量 18289753290 Informatica参数变量
    下面是本人通俗的理解，如有不对之处，希望指正 info参数的设置：在info中用到的参数都在server的专门的配置文件中（最好以parma）结尾 下面的GLOBAl就是全局的，$开头的是系统级变量，$$开头的变量是自定义变量。如果是在session中或者mapping中用到的变量就是局部变量，那就把global换成对应的session或者mapping名字。 [GLOBAL] $Par
  • python 解析unicode字符串为utf8编码字符串 酷的飞上天空 unicode
    php返回的json字符串如果包含中文，则会被转换成\uxx格式的unicode编码字符串返回。 在浏览器中能正常识别这种编码，但是后台程序却不能识别，直接输出显示的是\uxx的字符，并未进行转码。   转换方式如下   >>> import json >>> q = '{"text":"\u4
  • Hibernate的总结 永夜-极光 Hibernate
    1.hibernate的作用,简化对数据库的编码,使开发人员不必再与复杂的sql语句打交道   做项目大部分都需要用JAVA来链接数据库，比如你要做一个会员注册的 页面，那么 获取到用户填写的 基本信后，你要把这些基本信息存入数据库对应的表中，不用hibernate还有mybatis之类的框架，都不用的话就得用JDBC，也就是JAVA自己的，用这个东西你要写很多的代码，比如保存注册信
  • SyntaxError: Non-UTF-8 code starting with '\xc4' 随便小屋 python
    刚开始看一下Python语言，传说听强大的，但我感觉还是没Java强吧！ 写Hello World的时候就遇到一个问题，在Eclipse中写的，代码如下 ''' Created on 2014年10月27日 @author: Logic ''' print("Hello World!");  运行结果 SyntaxError: Non-UTF-8
  • 学会敬酒礼仪 不做酒席菜鸟 aijuans 菜鸟
    俗话说，酒是越喝越厚，但在酒桌上也有很多学问讲究，以下总结了一些酒桌上的你不得不注意的小细节。 细节一：领导相互喝完才轮到自己敬酒。敬酒一定要站起来，双手举杯。 细节二：可以多人敬一人，决不可一人敬多人，除非你是领导。 细节三：自己敬别人，如果不碰杯，自己喝多少可视乎情况而定，比如对方酒量，对方喝酒态度，切不可比对方喝得少，要知道是自己敬人。 细节四：自己敬别人，如果碰杯，一
  • 《创新者的基因》读书笔记 aoyouzi 读书笔记《创新者的基因》
    创新者的基因   创新者的“基因”，即最具创意的企业家具备的五种“发现技能”：联想，观察，实验，发问，建立人脉。   第一部分破坏性创新，从你开始 第一章破坏性创新者的基因 如何获得启示： 发现以下的因素起到了催化剂的作用：(1) -个挑战现状的问题；(2)对某项技术、某个公司或顾客的观察；(3) -次尝试新鲜事物的经验或实验；(4)与某人进行了一次交谈，为他点醒
  • 表单验证技术 百合不是茶 JavaScriptDOM对象String对象事件
    js最主要的功能就是验证表单,下面是我对表单验证的一些理解,贴出来与大家交流交流  ,数显我们要知道表单验证需要的技术点, String对象,事件,函数   一:String对象;通常是对字符串的操作;   1,String的属性;   字符串.length;表示该字符串的长度; var str= "java"
  • web.xml配置详解之context-param bijian1013 javaservletweb.xmlcontext-param
    一.格式定义： <context-param> <param-name>contextConfigLocation</param-name> <param-value>contextConfigLocationValue></param-value> </context-param> 作用：该元
  • Web系统常见编码漏洞（开发工程师知晓） Bill_chen sqlPHPWebfckeditor脚本
    1.头号大敌：SQL Injection 原因：程序中对用户输入检查不严格，用户可以提交一段数据库查询代码，根据程序返回的结果， 获得某些他想得知的数据，这就是所谓的SQL Injection，即SQL注入。 本质: 对于输入检查不充分，导致SQL语句将用户提交的非法数据当作语句的一部分来执行。 示例： String query = "SELECT id FROM users
  • 【MongoDB学习笔记六】MongoDB修改器 bit1129 mongodb
    本文首先介绍下MongoDB的基本的增删改查操作，然后，详细介绍MongoDB提供的修改器，以完成各种各样的文档更新操作  MongoDB的主要操作 show dbs 显示当前用户能看到哪些数据库 use foobar 将数据库切换到foobar show collections 显示当前数据库有哪些集合 db.people.update，update不带参数，可
  • 提高职业素养，做好人生规划 白糖_ 人生
      培训讲师是成都著名的企业培训讲师，他在讲课中提出的一些观点很新颖，在此我收录了一些分享一下。注：讲师的观点不代表本人的观点，这些东西大家自己揣摩。   1、什么是职业规划：职业规划并不完全代表你到什么阶段要当什么官要拿多少钱，这些都只是梦想。职业规划是清楚的认识自己现在缺什么，这个阶段该学习什么，下个阶段缺什么，又应该怎么去规划学习，这样才算是规划。  
  • 国外的网站你都到哪边看？ bozch 技术网站国外
    学习软件开发技术，如果没有什么英文基础，最好还是看国内的一些技术网站，例如：开源OSchina，csdn，iteye,51cto等等。 个人感觉如果英语基础能力不错的话，可以浏览国外的网站来进行软件技术基础的学习，例如java开发中常用的到的网站有apache.org 里面有apache的很多Projects,springframework.org是spring相关的项目网站,还有几个感觉不错的
  • 编程之美-光影切割问题 bylijinnan 编程之美
    package a; public class DisorderCount { /**《编程之美》“光影切割问题” * 主要是两个问题： * 1.数学公式（设定没有三条以上的直线交于同一点）： * 两条直线最多一个交点，将平面分成了4个区域； * 三条直线最多三个交点，将平面分成了7个区域； * 可以推出：N条直线 M个交点，区域数为N+M+1。
  • 关于Web跨站执行脚本概念 chenbowen00 Web安全跨站执行脚本
    跨站脚本攻击(XSS)是web应用程序中最危险和最常见的安全漏洞之一。安全研究人员发现这个漏洞在最受欢迎的网站,包括谷歌、Facebook、亚马逊、PayPal,和许多其他网站。如果你看看bug赏金计划,大多数报告的问题属于 XSS。为了防止跨站脚本攻击,浏览器也有自己的过滤器,但安全研究人员总是想方设法绕过这些过滤器。这个漏洞是通常用于执行cookie窃取、恶意软件传播,会话劫持,恶意重定向。在
  • [开源项目与投资]投资开源项目之前需要统计该项目已有的用户数 comsci 开源项目
            现在国内和国外,特别是美国那边,突然出现很多开源项目,但是这些项目的用户有多少,有多少忠诚的粉丝,对于投资者来讲,完全是一个未知数,那么要投资开源项目,我们投资者必须准确无误的知道该项目的全部情况,包括项目发起人的情况,项目的维持时间..项目的技术水平,项目的参与者的势力,项目投入产出的效益.....
  • oracle alert log file（告警日志文件） daizj oracle告警日志文件alert log file
    The alert log is a chronological log of messages and errors, and includes the following items: All internal errors (ORA-00600), block corruption errors (ORA-01578), and deadlock errors (ORA-00060)
  • 关于 CAS SSO 文章声明 denger SSO
    由于几年前写了几篇 CAS 系列的文章，之后陆续有人参照文章去实现，可都遇到了各种问题，同时经常或多或少的收到不少人的求助。现在这时特此说明几点： 1.  那些文章发表于好几年前了，CAS 已经更新几个很多版本了，由于近年已经没有做该领域方面的事情，所有文章也没有持续更新。 2. 文章只是提供思路，尽管 CAS 版本已经发生变化，但原理和流程仍然一致。最重要的是明白原理，然后
  • 初二上学期难记单词 dcj3sjt126com englishword
    lesson 课 traffic 交通 matter 要紧；事物 happy 快乐的，幸福的 second 第二的 idea 主意；想法；意见 mean 意味着 important 重要的，重大的 never 从来，决不 afraid 害怕 的 fifth 第五的 hometown 故乡，家乡 discuss 讨论；议论 east 东方的 agree 同意；赞成 bo
  • uicollectionview 纯代码布局, 添加头部视图 dcj3sjt126com Collection
    #import <UIKit/UIKit.h> @interface myHeadView : UICollectionReusableView { UILabel *TitleLable; } -(void)setTextTitle; @end #import "myHeadView.h" @implementation m
  • N 位随机数字串的 JAVA 生成实现 FX夜归人 javaMath随机数Random
    /** * 功能描述 随机数工具类<br /> * @author FengXueYeGuiRen * 创建时间 2014-7-25<br /> */ public class RandomUtil { // 随机数生成器 private static java.util.Random random = new java.util.R
  • Ehcache（09）——缓存Web页面 234390216 ehcache页面缓存
    页面缓存 目录 1       SimplePageCachingFilter 1.1      calculateKey 1.2      可配置的初始化参数 1.2.1     cach
  • spring中少用的注解@primary解析 jackyrong primary
    这次看下spring中少见的注解@primary注解，例子 @Component public class MetalSinger implements Singer{ @Override public String sing(String lyrics) { return "I am singing with DIO voice
  • Java几款性能分析工具的对比 lbwahoo java
    Java几款性能分析工具的对比 摘自：http://my.oschina.net/liux/blog/51800   在给客户的应用程序维护的过程中，我注意到在高负载下的一些性能问题。理论上，增加对应用程序的负载会使性能等比率的下降。然而，我认为性能下降的比率远远高于负载的增加。我也发现，性能可以通过改变应用程序的逻辑来提升，甚至达到极限。为了更详细的了解这一点，我们需要做一些性能
  • JVM参数配置大全 nickys jvm应用服务器
    JVM参数配置大全 /usr/local/jdk/bin/java -Dresin.home=/usr/local/resin -server -Xms1800M -Xmx1800M -Xmn300M -Xss512K -XX:PermSize=300M -XX:MaxPermSize=300M -XX:SurvivorRatio=8 -XX:MaxTenuringThreshold=5 -
  • 搭建 CentOS 6 服务器(14) - squid、Varnish rensanning varnish
    （一）squid 安装 # yum install httpd-tools -y # htpasswd -c -b /etc/squid/passwords squiduser 123456 # yum install squid -y 设置 # cp /etc/squid/squid.conf /etc/squid/squid.conf.bak # vi /etc/
  • Spring缓存注解@Cache使用 tom_seed spring
    参考资料 http://www.ibm.com/developerworks/cn/opensource/os-cn-spring-cache/ http://swiftlet.net/archives/774   缓存注解有以下三个： @Cacheable      @CacheEvict     @CachePut
  • dom4j解析XML时出现"java.lang.noclassdeffounderror: org/jaxen/jaxenexception"错误 xp9802
    java.lang.NoClassDefFoundError: org/jaxen/JaxenExc 关键字: java.lang.noclassdeffounderror: org/jaxen/jaxenexception 使用dom4j解析XML时，要快速获取某个节点的数据，使用XPath是个不错的方法，dom4j的快速手册里也建议使用这种方式 执行时却抛出以下异常： Exceptio
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他