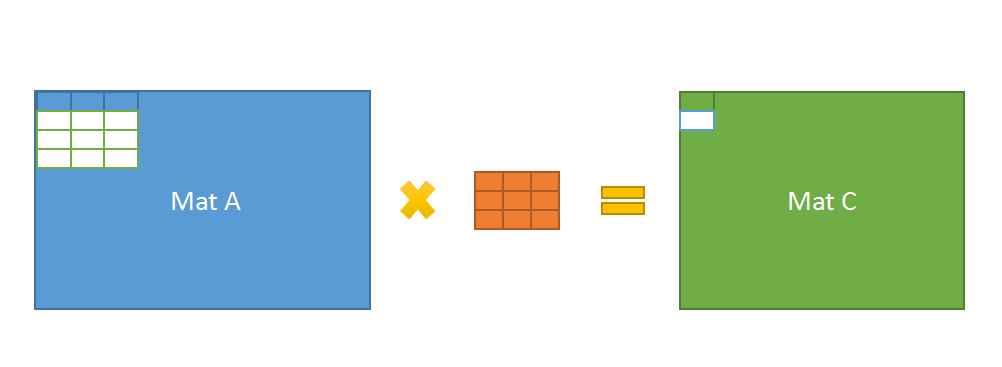ncnn 框架分析 openmp多核加速 缓存 仿存 cache 快速矩阵乘法 单指令多数据指令SIMD

ncnn 框架分析

本文github链接

博文末尾支持二维码赞赏哦 _

在ncnn中建立新层

ncnn 下载编译使用

参考1

参考2

1. param 和 bin 文件分析

param

  7767517   # 文件头 魔数
  75 83     # 层数量  输入输出blob数量
            # 下面有75行
  Input            data             0 1 data 0=227 1=227 2=3
  Convolution      conv1            1 1 data conv1 0=64 1=3 2=1 3=2 4=0 5=1 6=1728
  ReLU             relu_conv1       1 1 conv1 conv1_relu_conv1 0=0.000000
  Pooling          pool1            1 1 conv1_relu_conv1 pool1 0=0 1=3 2=2 3=0 4=0
  Convolution      fire2/squeeze1x1 1 1 pool1 fire2/squeeze1x1 0=16 1=1 2=1 3=1 4=0 5=1 6=1024
  ...
  层类型            层名字   输入blob数量 输出blob数量  输入blob名字 输出blob名字   参数字典
  
  参数字典，每一层的意义不一样：
  数据输入层 Input            data             0 1 data 0=227 1=227 2=3   图像宽度×图像高度×通道数量
  卷积层    Convolution  ...   0=64     1=3      2=1    3=2     4=0    5=1    6=1728           
           0输出通道数 num_output() ; 1卷积核尺寸 kernel_size();  2空洞卷积参数 dilation(); 3卷积步长 stride(); 
           4卷积填充pad_size();       5卷积偏置有无bias_term();   6卷积核参数数量 weight_blob.data_size()；
                                                              C_OUT * C_in * W_h * W_w = 64*3*3*3 = 1728
  池化层    Pooling      0=0       1=3       2=2        3=0       4=0
                      0池化方式:最大值、均值、随机     1池化核大小 kernel_size();     2池化核步长 stride(); 
                      3池化核填充 pad();   4是否为全局池化 global_pooling();
  激活层    ReLU       0=0.000000     下限阈值 negative_slope();
           ReLU6      0=0.000000     1=6.000000 上下限
  
  综合示例：
  0=1 1=2.5 -23303=2,2.0,3.0
  
  数组关键字 : -23300 
  -(-23303) - 23300 = 3 表示该参数在参数数组中的index
  后面的第一个参数表示数组元素数量，2表示包含两个元素

各层详细表格

// 参数读取 程序

// 读取字符串格式的 参数文件
int ParamDict::load_param(FILE* fp)
{
    clear();

//     0=100 1=1.250000 -23303=5,0.1,0.2,0.4,0.8,1.0

    // parse each key=value pair
    int id = 0;
    while (fscanf(fp, "%d=", &id) == 1)// 读取 等号前面的 key=========
    {
        bool is_array = id <= -23300;
        if (is_array)
        {
            id = -id - 23300;// 数组 关键字 -23300  得到该参数在参数数组中的 index
        }
        
// 是以 -23300 开头表示的数组===========
        if (is_array)
        {
            int len = 0;
            int nscan = fscanf(fp, "%d", &len);// 后面的第一个参数表示数组元素数量，5表示包含两个元素
            if (nscan != 1)
            {
                fprintf(stderr, "ParamDict read array length fail\n");
                return -1;
            }

            params[id].v.create(len);

            for (int j = 0; j < len; j++)
            {
                char vstr[16];
                nscan = fscanf(fp, ",%15[^,\n ]", vstr);//按格式解析字符串============
                if (nscan != 1)
                {
                    fprintf(stderr, "ParamDict read array element fail\n");
                    return -1;
                }

                bool is_float = vstr_is_float(vstr);// 检查该字段是否为 浮点数的字符串

                if (is_float)
                {
                    float* ptr = params[id].v;
                    nscan = sscanf(vstr, "%f", &ptr[j]);// 转换成浮点数后存入参数字典中
                }
                else
                {
                    int* ptr = params[id].v;
                    nscan = sscanf(vstr, "%d", &ptr[j]);// 转换成 整数后 存入字典中
                }
                if (nscan != 1)
                {
                    fprintf(stderr, "ParamDict parse array element fail\n");
                    return -1;
                }
            }
        }
// 普通关键字=========================
        else
        {
            char vstr[16];
            int nscan = fscanf(fp, "%15s", vstr);// 获取等号后面的 字符串
            if (nscan != 1)
            {
                fprintf(stderr, "ParamDict read value fail\n");
                return -1;
            }

            bool is_float = vstr_is_float(vstr);// 判断是否为浮点数

            if (is_float)
                nscan = sscanf(vstr, "%f", &params[id].f); // 读入为浮点数
            else
                nscan = sscanf(vstr, "%d", &params[id].i);// 读入为整数
            if (nscan != 1)
            {
                fprintf(stderr, "ParamDict parse value fail\n");
                return -1;
            }
        }

        params[id].loaded = 1;// 设置该 参数以及载入
    }

    return 0;
}

// 读取 二进制格式的 参数文件===================
int ParamDict::load_param_bin(FILE* fp)
{
    clear();

//     binary 0
//     binary 100
//     binary 1
//     binary 1.250000
//     binary 3 | array_bit
//     binary 5
//     binary 0.1
//     binary 0.2
//     binary 0.4
//     binary 0.8
//     binary 1.0
//     binary -233(EOP)

    int id = 0;
    fread(&id, sizeof(int), 1, fp);// 读入一个整数长度的 index

    while (id != -233)// 结尾
    {
        bool is_array = id <= -23300;
        if (is_array)
        {
            id = -id - 23300;// 数组关键字对应的 index
        }
// 是数组数据=======
        if (is_array)
        {
            int len = 0;
            fread(&len, sizeof(int), 1, fp);// 数组元素数量

            params[id].v.create(len);

            float* ptr = params[id].v;
            fread(ptr, sizeof(float), len, fp);// 按浮点数长度*数组长度 读取每一个数组元素====
        }
// 是普通数据=======
        else
        {
            fread(&params[id].f, sizeof(float), 1, fp);// 按浮点数长度读取 该普通字段对应的元素
        }

        params[id].loaded = 1;

        fread(&id, sizeof(int), 1, fp);// 读取 下一个 index
    }

    return 0;
}

bin

    +---------+---------+---------+---------+---------+---------+
    | weight1 | weight2 | weight3 | weight4 | ....... | weightN |
    +---------+---------+---------+---------+---------+---------+
    ^         ^         ^         ^
    0x0      0x80      0x140     0x1C0

  所有权重数据连接起来, 每个权重占 32bit

  权重数据 weight buffer

  [flag] (optional 可选)
  [raw data]
  [padding] (optional 可选)

      flag : unsigned int, little-endian, indicating the weight storage type, 
             0 => float32, 
             0x01306B47 => float16, 
             otherwise => quantized int8, 
                  may be omitted if the layer implementation forced the storage type explicitly。
      raw data : raw weight data, little-endian, 
                 float32 data or float16 data or quantized table 
                 and indexes depending on the storage type flag。
      padding : padding space for 32bit alignment, may be omitted if already aligned。

2. 轻模式

  开启轻模式省内存 set_light_mode(true)
  
  每个layer都会产生blob，除了最后的结果和多分支中间结果，大部分blob都不值得保留，
  开启轻模式可以在运算后自动回收，省下内存。
  
  举个例子：某网络结构为 A -> B -> C，在轻模式下，向ncnn索要C结果时，A结果会在运算B时自动回收，
  而B结果会在运算C时自动回收，最后只保留C结果，后面再需要C结果会直接获得，满足绝大部分深度网络的使用方式。

3. 网络和运算是分开的

  ncnn的net是网络模型，实际使用的是extractor，
  也就是同个net可以有很多个运算实例，而且运算实例互不影响，中间结果保留在extractor内部，
  在多线程使用时共用网络的结构和参数数据，初始化网络模型和参数只需要一遍.
  
  举个例子：全局静态的net实例，初始化一次后，就能不停地生成extractor使用.

4. openmp多核加速

// 使用OpenMP加速只需要在串行代码中添加编译指令以及少量API即可。

// 如下是一个向量相加的函数（串行）：

void add(const int* a, const int* b, int* c, const int len)
{
  for(int i=0; i<len; i++)
  {
    c[i] = a[i] + b[i];
  }
}

改成OpenMP多核加速（并行）：

#pragma omp parallel for 
// #pragma omp parallel for  num_threads(opt.num_threads);
void add(const int* a, const int* b, int* c, const int len)
{
  for(int i=0; i<len; i++)
  {
    c[i] = a[i] + b[i];
  }
}

// 理想情况下，加速比大约能达到0.75*cores。

5. 缓存，仿存，cache

缓存对于高速计算是非常重要的一环，通过合理的安排内存读写，能非常有效的加速计算。
数据存储一般是行优先存储，而cpu仿存，是会一次多读取当前内存后的连续几个地址中的数据。

如下面代码的gemm计算:

版本1：

static void gemm_v1(float* matA, float* matB, float* matC, const int M, const int N, const int K, const int strideA, const int strideB, const int strideC)
{
	for (int i = 0; i < N; i++)// 外层循环 为 列大小，会造成过多的仿存浪费!!!!
	{
		for (int j = 0; j < M; j++)
		{
			float sum = 0.0f;
			for (int k = 0; k < K; k++)
			{
				sum += matA[j*strideA + k] * matB[k*strideB + i];// 矩阵B 是列 访问
			}
			matC[j*strideC + i] = sum;// 矩阵C也是列 访问(j先变换，列方向)
		}
	}
}

版本2：

static void gemm_v2(float* matA, float* matB, float* matC, const int M, const int N, const int K, const int strideA, const int strideB, const int strideC)
{
	for (int i = 0; i < M; i++)// 外层循环 为 行主导，仿存效果好
	{
		for (int j = 0; j < N; j++)
		{
			float sum = 0.0f;
			for (int k = 0; k < K; k++)
			{
				sum += matA[i*strideA + k] * matB[k*strideB + j];// 只有矩阵B是列访问顺序
			}
			matC[i*strideC + j] = sum;
		}
	}
}

gemm_v1比gemm_v2速度会慢很多，尤其是数据量比较大的时候。
因为在gemm_v1中，matB和matC的访存以列为方向，会出现很多cache不命中的情况。
而在gemm_v2中则只有matB发生较多cache不命中，而这是gemm计算无法避免的。

在ncnn中，没有将输入和输出展开成两个大矩阵，会比较耗费内存；
就是按照卷积的方式，每次只读取，运算的部分内容。
以卷积计算conv3x3_s1为例，
每次从matA同时访问4行（一般一次3x3卷积只需要访问3行），
由于step是1，所以可以同时生成2行的convolution结果。
可以看到有2行数据直接共用了，缓存利用率得到极大提高。

快速矩阵乘法 参考

6. 单指令多数据指令SIMD 优化

SIMD即单指令多数据指令，
目前在x86平台下有MMX/SSE/AVX系列指令，
arm平台下有NEON指令。
一般SIMD指令通过intrinsics或者汇编实现。

SSE参考

SSE指令参考

neno参考

x86下 SSE编程

使用SSE指令，首先要了解这一类用于进行初始化加载数据以及将暂存器的数据保存到内存相关的指令，
我们知道，大多数SSE指令是使用的xmm0到xmm8的暂存器，
那么使用之前，就需要将数据从内存加载到这些暂存器。

数据的载入与保存

 1. load系列，用于加载数据，从内存到暂存器。 ====传入指针====
__m128 _mm_load_ss (float *p)   128字节暂存器， 4*32=128
     用于scalar的加载，所以，加载一个单精度浮点数到暂存器的低字节，
     其它三个单浮点单元清0，（r0 := *p, r1 := r2 := r3 := 0.0）。
     
__m128 _mm_load_ps (float *p)
     用于packed的加载（下面的都是用于packed的），要求p的地址是16字节对齐，否则读取的结果会出错，
     （r0 := p[0], r1 := p[1], r2 := p[2], r3 := p[3]）。
     
__m128 _mm_load1_ps (float *p)
__m128 _mm_loadh_pi (__m128 a, __m64 *p)
__m128 _mm_loadl_pi (__m128 a, __m64 *p)
__m128 _mm_loadr_ps (float *p)
__m128 _mm_loadu_ps (float *p)

 2. set系列，用于加载数据，大部分需要多条指令完成，但是可能不需要16字节对齐。 =====传入值====
__m128 _mm_set_ss (float w)   
     对应于_mm_load_ss的功能，不需要字节对齐，需要多条指令。（r0 = w, r1 = r2 = r3 = 0.0）
__m128 _mm_set_ps (float z, float y, float x, float w)
     对应于_mm_load_ps的功能，参数是四个单独的单精度浮点数，所以也不需要字节对齐，需要多条指令。
     （r0=w, r1 = x, r2 = y, r3 = z，注意顺序） 
__m128 _mm_set1_ps (float w)
     对应于_mm_load1_ps的功能，不需要字节对齐，需要多条指令。（r0 = r1 = r2 = r3 = w）
__m128 _mm_setr_ps (float z, float y, float x, float w)
__m128 _mm_setzero_ps ()
         是清0操作，只需要一条指令。（r0 = r1 = r2 = r3 = 0.0）
     
 3.  store系列，用于将计算结果等SSE暂存器的数据保存到内存中。
void _mm_store_ss (float *p, __m128 a)     _mm_store_ss：一条指令，*p = a0
void _mm_store_ps (float *p, __m128 a)     一条指令，p[i] = a[i]
void _mm_store1_ps (float *p, __m128 a)
void _mm_storeh_pi (__m64 *p, __m128 a)
void _mm_storel_pi (__m64 *p, __m128 a)
void _mm_storer_ps (float *p, __m128 a)
void _mm_storeu_ps (float *p, __m128 a)   一条指令，p[i] = a[i]，不要求16字节对齐。
void _mm_stream_ps (float *p, __m128 a)   直接写入内存，不改变cache的数据。
这一系列函数和load系列函数的功能对应，基本上都是一个反向的过程。

计算指令

SSE提供了大量的浮点运算指令，包括加法、减法、乘法、除法、开方、最大值、最小值、近似求倒数、求开方的倒数等等，
可见SSE指令的强大之处。那么在了解了上面的数据加载和数据保存的指令之后，使用这些算术指令就很容易了，下面以加法为例。

SSE中浮点加法的指令有：
	__m128 _mm_add_ss (__m128 a, __m128 b)； // a =(a0,a1,a2,a3)  b = (b0,b1,b2,b3) 结果=(a0+b0,a1,a2,a3)
	__m128 _mm_add_ps (__m128 a, __m128 b)； // 结果=(a0+b0, a1+b1, a2+b2, a3+b3)
	其中，_mm_add_ss表示scalar执行模式，_mm_add_ps表示packed执行模式。

减法指令:
 	__m128 _mm_sub_ss (__m128 a, __m128 b); // 结果=(a0-b0,a1,a2,a3)
        __m128 _mm_sub_ps (__m128 a, __m128 b); // 结果=(a0-b0, a1-b1, a2-b2, a3-b3)
    乘法指令：
        __m128 _mm_mul_ss (__m128 a, __m128 b); 
	__m128 _mm_mul_ps (__m128 a, __m128 b);// 结果=(a0*b0, a1*b1, a2*b2, a3*b3)
    除法指令:
        __m128 _mm_div_ss (__m128 a, __m128 b); 
	__m128 _mm_div_ps (__m128 a, __m128 b);// 结果=(a0/b0, a1/b1, a2/b2, a3/b3)    
 加减混合运算：
        __m128 _mm_addsub_ps (__m128 a, __m128 b);  // 结果=(a0-b0, a1+b1, a2-b3, a3+b3)
 开平方 sqrt  去倒数 rcp 平方根的倒数 rsqrt 最小值min 最大值max
 
	
般而言，使用SSE指令写代码，
步骤为：1. 使用load/set函数将数据从内存加载到SSE暂存器；
       2. 使用相关SSE指令完成计算等；
       3. 使用store系列函数将结果从暂存器保存到内存，供后面使用。

// 示例程序
	float op1[4] = {1.0, 2.0, 3.0, 4.0}; // 浮点数数组
	float op2[4] = {1.0, 2.0, 3.0, 4.0};
	float result[4];// 结果数组

	__m128  a;
	__m128  b;
	__m128  c;

	// 1. Load  将数据从内存载入到 暂存器
	a = _mm_loadu_ps(op1);
	b = _mm_loadu_ps(op2);

	// 2. Calculate 进行逻辑计算
	c = _mm_add_ps(a, b);	// c = a + b

	// 3. Store 将数据从暂存器 保存到 内存
	_mm_storeu_ps(result, c);

	/*		// Using the __m128 union to get the result.
	printf("0: %lf\n", c.m128_f32[0]);
	printf("1: %lf\n", c.m128_f32[1]);
	printf("2: %lf\n", c.m128_f32[2]);
	printf("3: %lf\n", c.m128_f32[3]);
	*/
	printf("0: %lf\n", result[0]);
	printf("1: %lf\n", result[1]);
	printf("2: %lf\n", result[2]);
	printf("3: %lf\n", result[3]);

ARM 下 NENO编程

ARM CPU最开始只有普通的寄存器，可以进行基本数据类型的基本运算。
自ARMv5开始引入了VFP（Vector Floating Point）指令，该指令用于向量化加速浮点运算。
自ARMv7开始正式引入NEON指令，NEON性能远超VFP，因此VFP指令被废弃。

ARMV7架构包含：

16个通用寄存器（32bit）， R0-R15， R13为栈顶指针 Stack pointer, R14为Link registr, R15为程序计数器 Program Counter
16个NEON寄存器（128bit），Q0-Q15（同时也可以被视为32个64bit的寄存器，D0-D31）
16个VFP寄存器（32bit），  S0-S15
NEON和VFP的区别在于VFP是加速浮点计算的硬件不具备数据并行能力，同时VFP更尽兴双精度浮点数（double）的计算，NEON只有单精度浮点计算能力。

NEON指令和数据类型介绍

neon 和 sse综合示例程序

项目工程

// 1. 在容器中填充随机数===========

// 生成器generator：能够产生离散的等可能分布数值
// 分布器distributions: 能够把generator产生的均匀分布值映射到其他常见分布，
//                     如均匀分布uniform，正态分布normal，二项分布binomial，泊松分布poisson
static void fill_random_value(std::vector<float>& vec_data)
{        
        // 浮点数均匀分布 分布器    uniform_int_distribution(整数均匀分布)
	std::uniform_real_distribution<float> distribution(
		std::numeric_limits<float>::min(),
		std::numeric_limits<float>::max());
        // 随机数 生成器
	std::default_random_engine generator;
        // std::default_random_engine generator(time(NULL));// 配合随机数种子
	
        // 为 vec_data 生成随机数，传入首尾迭代器和一个 lambda匿名函数
	// [变量截取](参数表){函数提体}； [&](){}, 中括号内的& 表示函数可使用函数外部的变量。
	std::generate(vec_data.begin(), vec_data.end(), [&]() { return distribution(generator); });
}
// 下面是各种变量截取的选项：
//   [] 不截取任何变量
//   [&} 截取外部作用域中所有变量，并作为引用在函数体中使用
//   [=] 截取外部作用域中所有变量，并拷贝一份在函数体中使用
//   [=, &foo]   截取外部作用域中所有变量，并拷贝一份在函数体中使用，但是对foo变量使用引用
//   [bar]       截取bar变量并且拷贝一份在函数体重使用，同时不截取其他变量
//   [this]      截取当前类中的this指针。如果已经使用了&或者=就默认添加此选项。


// 2. 判断两vector是否相等====================================
static bool is_equals_vector(const std::vector<float>& vec_a, const std::vector<float>& vec_b)
{
	// 首先判断 大小是否一致
	if (vec_a.size() != vec_b.size())
		return false;
        for (size_t i=0; i<vec_a.size(); i++)
	{
		if(vec_a[i] != vec_b[i]) // 浮点数可以这样 判断不相等？？
			return false;
	}
	// 每个元素均相等
 	return true;
}

// 3. 正常的vector相乘(需要关闭编译器的自动向量优化)====================
static void normal_vector_mul(const std::vector<float>& vec_a, 
                              const std::vector<float>& vec_b, 
			      std::vector<float>& vec_result)
{
	// 检查 数组维度
	assert(vec_a.size() == vec_b.size());
	assert(vec_a.size() == vec_result.size());
	
	// 循环遍历相乘  编译器可能会自动 进行向量化优化  添加标志进行关闭 -ftree-vectorize
	for (size_t i=0; i<vec_result.size(); i++)
		vec_result[i] = vec_a[i] * vec_b[i];
}


// 4. neon优化的vector相乘======================================
static void neon_vector_mul(const std::vector<float>& vec_a, 
                              const std::vector<float>& vec_b, 
			      std::vector<float>& vec_result)
{
	// 检查 数组维度
	assert(vec_a.size() == vec_b.size());
	assert(vec_a.size() == vec_result.size());
	
	// noon 寄存器操作
	int i = 0;
	for (; i < (int)vec_result.size() - 3 ; i+=4)// 一次运算四个
	{
		const auto data_a = vld1q_f32(&vec_a[i]);// 放入寄存器
		const auto data_b = vld1q_f32(&vec_b[i]);// 放入寄存器

		float* dst_ptr = &vec_result[i]; // 结果矩阵 指针

		const auto data_res = vmulq_f32(data_a, data_b); // 32为寄存器 浮点数乘法

		vst1q_32(dst_ptr, data_res);// 将 寄存器乘法结果 复制到 结果数组中
	}
}

// 这段代码中使用了3条NEON指令：vld1q_f32，vmulq_f32，vst1q_f32

// 5.  sse 优化程序=========================================
static void sse_vector_mul(const std::vector<float>& vec_a, 
                           const std::vector<float>& vec_b, 
			   std::vector<float>& vec_result)
{
	// 检查 数组维度
	assert(vec_a.size() == vec_b.size());
	assert(vec_a.size() == vec_result.size());
	
	// sse 寄存器操作
        int i=0;
        for(; i<vec_result.size()-3; i+=4)
	{
		// 1. load 数据从内存载入暂存器
		__m128  a = _mm_loadu_ps(&vec_a[i]);
	        __m128  b = _mm_loadu_ps(&vec_b[i]);
		__m128  res;

	        float* dst_ptr = &vec_result[i]; // 结果矩阵 指针
                // 2. 进行计算
		res = _mm_mul_ps(a, b); // 32为寄存器 浮点数乘法
	        // 3. 将计算结果 从暂存器 保存到 内存  res ----> dst_ptr
		_mm_storeu_ps(dst_ptr, res);
	}
}

7. src目录分析

/src目录：
    目录顶层下是一些基础代码，如宏定义，平台检测，mat数据结构，layer定义，blob定义，net定义等。
    	platform.h.in 平台检测
	benchmark.cpp benchmark.h 测试各个模型的执行速度
            allocator.cpp allocator.h 内存对齐
	paramdict.cpp paramdict.h 层参数解析 读取二进制格式、字符串格式、密文格式的参数文件
	opencv.cpp opencv.h       opencv 风格的数据结构 的 最小实现
	                          大小结构体 Size 
				  矩阵框结构体 Rect_ 交集 并集运算符重载
				  点结构体     Point_
				  矩阵结构体   Mat     深拷贝 浅拷贝 获取指定矩形框中的roi 读取图像 写图像 双线性插值算法改变大小
        mat.cpp mat.h             3维矩阵数据结构, 在层间传播的就是Mat数据，Blob数据是花架子
	                          substract_mean_normalize(); 去均值并归一化
				  half2float();               float16 的 data 转换成 float32 的 data
				  copy_make_border();         矩阵周围填充
				  resize_bilinear_image();    双线性插值
	modelbin.cpp modelbin.h   从文件中载入模型权重、从内存中载入、从数组中载入
	layer.cpp layer.h         层接口，四种前向传播接口函数
	Blob数据是花架子
	
	net.cpp net.h             ncnn框架接口：
	                          注册 用户定义的新层 Net::register_custom_layer();
	                          网络载入 模型参数   Net::load_param();
				  载入     模型权重   Net::load_model();
				  网络blob 输入       Net::input();
				  网络前向传          Net::forward_layer();    被Extractor::extract() 执行
				  创建网络模型提取器   Net::create_extractor();
	                          模型提取器提取某一层输出 Extractor::extract();
				  
    ./src/layer下是所有的layer定义代码
    ./src/layer/arm是arm下的计算加速的layer
    ./src/layer/x86是x86下的计算加速的layer。

ncnn 支持的层

├── absval.cpp                       // 绝对值层
├── absval.h
├── argmax.cpp                       // 最大值层
├── argmax.h
├── arm ============================ arm平台下的层
│   ├── absval_arm.cpp               // 绝对值层
│   ├── absval_arm.h
│   ├── batchnorm_arm.cpp            // 批归一化 去均值除方差
│   ├── batchnorm_arm.h
│   ├── bias_arm.cpp                 // 偏置
│   ├── bias_arm.h
│   ├── convolution_1x1.h            // 1*1 float32 卷积
│   ├── convolution_1x1_int8.h       // 1*1 int8    卷积
│   ├── convolution_2x2.h            // 2*2 float32 卷积
│   ├── convolution_3x3.h            // 3*3 float32 卷积
│   ├── convolution_3x3_int8.h       // 3*3 int8    卷积
│   ├── convolution_4x4.h            // 4*4 float32 卷积
│   ├── convolution_5x5.h            // 5*5 float32 卷积
│   ├── convolution_7x7.h            // 7*7 float32 卷积
│   ├── convolution_arm.cpp          // 卷积层
│   ├── convolution_arm.h
│   ├── convolutiondepthwise_3x3.h      // 3*3 逐通道 float32 卷积
│   ├── convolutiondepthwise_3x3_int8.h // 3*3 逐通道 int8    卷积 
│   ├── convolutiondepthwise_arm.cpp    // 逐通道卷积
│   ├── convolutiondepthwise_arm.h
│   ├── deconvolution_3x3.h             // 3*3 反卷积
│   ├── deconvolution_4x4.h             // 4*4 反卷积
│   ├── deconvolution_arm.cpp           // 反卷积
│   ├── deconvolution_arm.h
│   ├── deconvolutiondepthwise_arm.cpp  // 反逐通道卷积
│   ├── deconvolutiondepthwise_arm.h
│   ├── dequantize_arm.cpp              // 反量化
│   ├── dequantize_arm.h
│   ├── eltwise_arm.cpp                 // 逐元素操作，product(点乘), sum(相加减) 和 max(取大值)
│   ├── eltwise_arm.h
│   ├── innerproduct_arm.cpp            // 即 fully_connected (fc)layer, 全连接层
│   ├── innerproduct_arm.h
│   ├── lrn_arm.cpp                     // Local Response Normalization，即局部响应归一化层
│   ├── lrn_arm.h
│   ├── neon_mathfun.h                  // neon 数学函数库
│   ├── pooling_2x2.h                   // 2*2 池化层
│   ├── pooling_3x3.h                   // 3*3 池化层
│   ├── pooling_arm.cpp                 // 池化层
│   ├── pooling_arm.h
│   ├── prelu_arm.cpp                   // (a*x,x) 前置relu激活层
│   ├── prelu_arm.h
│   ├── quantize_arm.cpp                // 量化层
│   ├── quantize_arm.h
│   ├── relu_arm.cpp                    // relu 层 (0,x)
│   ├── relu_arm.h
│   ├── scale_arm.cpp                   // BN层后的 平移和缩放层 scale
│   ├── scale_arm.h
│   ├── sigmoid_arm.cpp                 // sigmod 负指数倒数归一化 激活层  1/（1 + e^(-zi)）
│   ├── sigmoid_arm.h
│   ├── softmax_arm.cpp                 // softmax 指数求和归一化 激活层   e^(zi) / sum(e^(zi))
│   └── softmax_arm.h
|
|
|================================ 普通平台 x86等，待优化=============
├── batchnorm.cpp             // 批归一化 去均值除方差
├── batchnorm.h
├── bias.cpp                  // 偏置
├── bias.h
├── binaryop.cpp              // 二元操作: add，sub， div， mul，mod等
├── binaryop.h
├── bnll.cpp                  // 
├── bnll.h
├── clip.cpp                  // 通道分路
├── clip.h
├── concat.cpp                // 通道叠加
├── concat.h
├── convolution.cpp           // 普通卷积层
├── convolutiondepthwise.cpp  // 逐通道卷积
├── convolutiondepthwise.h
├── convolution.h 
├── crop.cpp                  // 剪裁层
├── crop.h
├── deconvolution.cpp         // 反卷积
├── deconvolutiondepthwise.cpp// 反逐通道卷积
├── deconvolutiondepthwise.h
├── deconvolution.h
├── dequantize.cpp            // 反量化
├── dequantize.h
├── detectionoutput.cpp       // ssd 的检测输出层================================
├── detectionoutput.h
├── dropout.cpp               // 随机失活层
├── dropout.h
├── eltwise.cpp               // 逐元素操作， product(点乘), sum(相加减) 和 max(取大值)
├── eltwise.h
├── elu.cpp                   // 指数线性单元relu激活层 Prelu : (a*x, x) ----> Erelu : (a*(e^x - 1), x) 
├── elu.h
├── embed.cpp                 // 嵌入层，用在网络的开始层将你的输入转换成向量
├── embed.h
├── expanddims.cpp            // 增加维度
├── expanddims.h
├── exp.cpp                   // 指数映射
├── exp.h
├── flatten.cpp               // 摊平层
├── flatten.h
├── innerproduct.cpp          // 全连接层
├── innerproduct.h
├── input.cpp                 // 数据输入层
├── input.h
├── instancenorm.cpp          // 单样本 标准化 规范化
├── instancenorm.h
├── interp.cpp                // 插值层 上下采样等
├── interp.h
├── log.cpp                   // 对数层
├── log.h
├── lrn.cpp                   // Local Response Normalization，即局部响应归一化层
├── lrn.h                     // 对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，
|                             // 并抑制其他反馈较小的神经元，增强了模型的泛化能力
├── lstm.cpp                
├── lstm.h                    // lstm 长短词记忆层
├── memorydata.cpp            // 内存数据层
├── memorydata.h
├── mvn.cpp
├── mvn.h
├── normalize.cpp             // 归一化
├── normalize.h
├── padding.cpp               // 填充，警戒线
├── padding.h
├── permute.cpp               //  ssd 特有层 交换通道顺序 [bantch_num, channels, h, w] ---> [bantch_num, h, w, channels]]=========
├── permute.h
├── pooling.cpp               // 池化层
├── pooling.h
├── power.cpp                 // 平移缩放乘方 : (shift + scale * x) ^ power
├── power.h
├── prelu.cpp                 // Prelu  (a*x,x)
├── prelu.h
├── priorbox.cpp              // ssd 独有的层 建议框生成层 L1 loss 拟合============================
├── priorbox.h
├── proposal.cpp              // faster rcnn 独有的层 建议框生成，将rpn网络的输出转换成建议框======== 
├── proposal.h
├── quantize.cpp              // 量化层
├── quantize.h
├── reduction.cpp             // 将输入的特征图按照给定的维度进行求和或求平均
├── reduction.h
├── relu.cpp                  // relu 激活层： (0,x)
├── relu.h
├── reorg.cpp                 // yolov2 独有的层， 一拆四层，一个大矩阵，下采样到四个小矩阵=================
├── reorg.h
├── reshape.cpp               // 变形层： 在不改变数据的情况下，改变输入的维度
├── reshape.h
├── rnn.cpp                   // rnn 循环神经网络
├── rnn.h
├── roipooling.cpp            // faster Rcnn 独有的层， ROI池化层： 输入m*n 均匀划分成 a*b个格子后池化，得到固定长度的特征向量 ==========
├── roipooling.h
├── scale.cpp                 // bn 层之后的 平移缩放层
├── scale.h
├── shufflechannel.cpp        // ShuffleNet 独有的层，通道打乱，通道混合层=================================
├── shufflechannel.h
├── sigmoid.cpp               // 负指数倒数归一化层  1/(1 + e^(-zi))
├── sigmoid.h
├── slice.cpp                 // concat的反向操作， 通道分开层，适用于多任务网络
├── slice.h
├── softmax.cpp               // 指数求和归一化层  e^(zi) / sum(e^(zi))
├── softmax.h
├── split.cpp                 // 将blob复制几份，分别给不同的layer，这些上层layer共享这个blob。
├── split.h
├── spp.cpp                   // 空间金字塔池化层 1+4+16=21 SPP-NET 独有===================================
├── spp.h
├── squeeze.cpp               // squeezeNet独有层， Fire Module, 一层conv层变成两层：squeeze层+expand层, 1*1卷积---> 1*1 + 3*3=======
├── squeeze.h
├── tanh.cpp                  // 双曲正切激活函数  (e^(zi) - e^(-zi)) / (e^(zi) + e^(-zi))
├── tanh.h
├── threshold.cpp             // 阈值函数层
├── threshold.h
├── tile.cpp                  // 将blob的某个维度，扩大n倍。比如原来是1234，扩大两倍变成11223344。
├── tile.h
├── unaryop.cpp               // 一元操作: abs， sqrt， exp， sin， cos，conj（共轭）等
├── unaryop.h
|
|==============================x86下特殊的优化层=====
├── x86
│   ├── avx_mathfun.h                    // x86 数学函数
│   ├── convolution_1x1.h                // 1*1 float32 卷积
│   ├── convolution_1x1_int8.h           // 1×1 int8 卷积
│   ├── convolution_3x3.h                // 3*3 float32 卷积
│   ├── convolution_3x3_int8.h           // 3×3 int8 卷积
│   ├── convolution_5x5.h                // 5*5 float32 卷积 
│   ├── convolutiondepthwise_3x3.h       // 3*3 float32 逐通道卷积
│   ├── convolutiondepthwise_3x3_int8.h  // 3*3 int8 逐通道卷积
│   ├── convolutiondepthwise_x86.cpp     //  逐通道卷积
│   ├── convolutiondepthwise_x86.h
│   ├── convolution_x86.cpp              //  卷积
│   ├── convolution_x86.h
│   └── sse_mathfun.h                    // sse优化 数学函数
├── yolodetectionoutput.cpp              // yolo-v2 目标检测输出层=========================================
└── yolodetectionoutput.h

caffe中layer的一些特殊操作，比如split

slice：在某一个维度，按照给定的下标，blob拆分成几块。
       比如要拆分channel，总数50，下标为10,20,30,40，
       那就是分成5份，每份10个channel，输出5个layer。

concat：在某个维度，将输入的layer组合起来，是slice的逆过程。

split：将blob复制几份，分别给不同的layer，这些上层layer共享这个blob。

tile：将blob的某个维度，扩大n倍。比如原来是1234，扩大两倍变成11223344。

reduction：将某个维度缩减至1维，方法可以是sum、mean、asum、sumsq。

reshape：这个很简单，就是matlab里的reshape。

eltwise：将几个同样大小的layer，合并为1个，合并方法可以是相加、相乘、取最大。

flatten：将中间某几维合并，其实可以用reshape代替。

reshape 变形

# 假设原数据为：32*3*28*28， 表示32张3通道的28*28的彩色图片
 reshape_param {
   shape {
   dim: 0  32->32 # 0表示和原来一致
   dim: 0  3->3
   dim: 14 28->14
   dim: -1 #让其推断出此数值
   }
}
# 输出数据为：32*3*14*56