ELMo论文解读
论文链接:https://arxiv.org/abs/1802.05365
此论文提出了一种新的表示词语的方法,用于解决如下问题:
(1) 词的复杂特征
(2) 在不同语境下词的多义性
该论文提出的模型,使用biLM(双向语言模型)在大型语料上进行预训练,通过内部隐藏状态得到词向量,这种表示可以很容易的用在已经存在的模型并明显提高解决NLP任务的能力,包括问答、情感分析等等。
1. 介绍
得到高质量的词表征方法存在难点,要基于:(1)词的复杂特征(句法和语义)(2)词在不同上下文中的含义(多义词),ELMo的目的是解决这两个难点。和传统的词嵌入不同,其他模型只用最后一层的输出值来作为word embedding的值,ELMo每个词向量是双向语言模型内部隐藏状态特征的线性组合,由一个基于大量文本训练的双向语言模型而得到的,该方法由此得到命名:ELMo(Embeddings from Language Models)。
结合内部状态使得词向量能表达的信息更加丰富,具体来看,LSTM上面的层次能够捕捉词义与上下文相关的方面(可以用来消歧),而下面的层次可以捕捉句法方面的信息(可以用来作词性标注)。
2. ELMo: Embeddings from Language Models
2.1 双向语言模型(biLM)
假设有N个词组成的词序列( t 1 t_1 t1, t 2 t_2 t2,…, t N t_N tN),前向语言模型计算词 t k t_k tk的概率使用它前面的词序列( t 1 t_1 t1到 t k − 1 t_k-1 tk−1):
p ( t 1 , t 2 , . . . t N ) = ∏ k = 1 N p ( t k ∣ t 1 , t 2 , . . , t k − 1 ) p(t_1,t_2,...t_N)=\prod_{k=1}^Np(t_k\vert t_1,t_2,..,t_{k-1}) p(t1,t2,...tN)=∏k=1Np(tk∣t1,t2,..,tk−1)
用 X k L M X_k^{LM} XkLM来表示与上下文无关的词向量,然后将其传入L层的前向LSTMs,在每个位置k,每个LSTM层输出一个 h ⇀ k , j L M \overset\rightharpoonup h_{k,j}^{LM} h⇀k,jLM(j从1到L),顶层的输出( h ⇀ k , L L M \overset\rightharpoonup h_{k,L}^{LM} h⇀k,LLM)通过softmax函数用来预测下一个词 t k + 1 t_k+1 tk+1
一个反向的LM与前向LM类似,只不过是用反方向跑一遍输入序列,概率用下面的公式计算:
p ( t 1 , t 2 , . . . t N ) = ∏ k = 1 N p ( t k ∣ t k + 1 , t k + 2 , . . , t N ) p(t_1,t_2,...t_N)=\prod_{k=1}^Np(t_k\vert t_{k+1},t_{k+2},..,t_N) p(t1,t2,...tN)=∏k=1Np(tk∣tk+1,tk+2,..,tN)
与前向LM类似,后向LSTM位置k第j层(共L层)用 h ↼ k , j L M \overset\leftharpoonup h_{k,j}^{LM} h↼k,jLM表示;biLM结合了前向LM和后向LM,目标是最大化前后向对数似然函数:
∑ k = N ( log p ( t k ∣ t 1 , . . . , t k − 1 ; Θ x , Θ → L S T M , Θ s ) + log p ( t k ∣ t k + 1 , . . . , t N ; Θ x , Θ ← L S T M , Θ s ) ) \sum_{k=}^N(\log p(t_k\vert t_1,...,t_{k-1};\Theta_x,{\overrightarrow\Theta}_{LSTM},\Theta_s)+\log p(t_k\vert t_{k+1},...,t_N;\Theta_x,{\overleftarrow\Theta}_{LSTM},\Theta_s)) ∑k=N(logp(tk∣t1,...,tk−1;Θx,ΘLSTM,Θs)+logp(tk∣tk+1,...,tN;Θx,ΘLSTM,Θs))
将前向和后向中用于词表示和用于Softmax的参数联系起来,也就是说,在两个方向共享了一些权重参数,而不是使用完全独立的参数
biLM模型结构如下(图画了半天,又丑又菜):
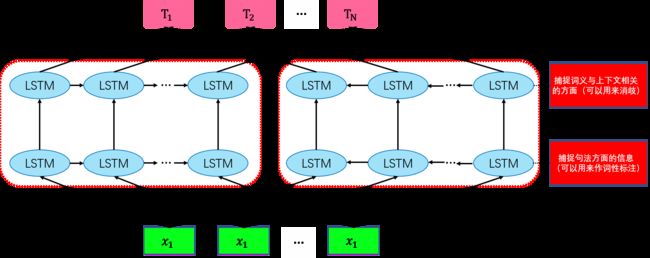
2.2 ELMo
接下来就是ELMo的核心了,首先ELMo是biLM内部中间层的组合,对于每个词,一个L层的biLM要计算出2L+1个表示:
R k = { x k L M , h → k , j L M , h ← k , j L M j = 1 , . . . , L } = { h k , j L M ∣ j = 0 , . . . , L } R_k=\{x_k^{LM},\overrightarrow h_{k,j}^{LM},\overleftarrow h_{k,j}^{LM}j=1,...,L\}=\{h_{k,j}^{LM}\vert j=0,...,L\} Rk={xkLM,hk,jLM,hk,jLMj=1,...,L}={hk,jLM∣j=0,...,L}
其中, h k , 0 L M h_{k,0}^{LM} hk,0LM表示直接编码的结果,对于每个biLSTM层, h k , j L M h_{k,j}^{LM} hk,jLM= [ h ⇀ k , j L M \overset\rightharpoonup h_{k,j}^{LM} h⇀k,jLM, h ↼ k , j L M \overset\leftharpoonup h_{k,j}^{LM} h↼k,jLM] ,其中k表示序列中的位置,j表示第j层
为了应用到其他模型中,ELMo将所有层的输出结果整合入一个向量: E L M o k = E ( R k ; Θ e ) ELMo_k=E(R_k;\Theta_e) ELMok=E(Rk;Θe);最简单的一种情况,就是ELMo只选择最顶层,即 E ( R k ) = h k , L L M E(R_k)=h_{k,L}^{LM} E(Rk)=hk,LLM;一般来说,ELMo利用每层状态的线性组合,针对于某个任务通过所有的biLM层得到:
E L M o k t a s k = E ( R k ; Θ t a s k ) = γ t a s k ∑ j = 0 L s j t a s k h k , j L M ELMo_k^{task}=E(R_k;\Theta^{task})=\gamma^{task}\sum_{j=0}^Ls_j^{task}h_{k,j}^{LM} ELMoktask=E(Rk;Θtask)=γtask∑j=0Lsjtaskhk,jLM
上式中, s s t a c k s^{stack} sstack是softmax-normalized weights,标量参数γ允许任务模型缩放整个ELMo向量(γ在优化过程中很重要,因为ELMo生成词向量的方式和任务所需存在一定的差异;个人觉得,这种差异就如前文所分析的,LSTM高层与底层所捕捉的信息是存在差异的),每个biLM层的激活有着不同的分布,在一定程度上对每一层可以提供一些标准化的效果
2.3 如何在有监督的NLP任务中使用biLMS
大部分有监督NLP模型在最底层有着大致相同的结构,可以用一致、统一的方式添加ELMo,论文中大致体现了三种使用方法:
- 保持biLM的权重不变,连接 E L M o k t a s k ELMo_k^{task} ELMoktask和初始词向量 x k x_k xk,并将[ x k x_k xk, E L M o k t a s k ELMo_k^{task} ELMoktask]传入任务的RNN中
- 在任务使用的RNN中,RNN的输出加入 E L M o k t a s k ELMo_k^{task} ELMoktask,形成[ h k h_k hk, E L M o k t a s k ELMo_k^{task} ELMoktask]
- 在ELMo中使用适当数量的dropout,并在损失中添加 λ ∣ ∣ w ∣ ∣ 2 2 \lambda\vert\vert w\vert\vert_2^2 λ∣∣w∣∣22
2.4 预训练过程
在作者的预训练过程中,用了两层的biLSTM,共计4096个单元,输出纬度为512,并且第一层和第二层之间有residual connection,包括最初的那一层文本向量(上下文不敏感类型的词表征使用2048个字符卷积filter,紧接着两层highway layers)整个ELMO会为每一个词提供一个3层的表示(下游模型学习的就是这3层输出的组合),下游模型而传统的词嵌入方法只为词提供了一层表示。另外,作者提出,对该模型进行FINE-TUNE训练的话,对具体的NLP任务会有提升的作用。
经过预训练后,biLM可为任一任务计算词的表示。在某些情况下,对biLM进行fine tuning会对NLP任务有所帮助。
注:关于residual connection和highway layers:residual connection和highway layers这两种结构都能让一部分的数据可以跳过某些变换层的运算,直接进入下一层,区别在于highway需要一个权值来控制每次直接通过的数据量,而residual connection直接让一部分数据到达了下一层
3 总结
- ELMo着重解决一词多义,相比较于传统的word2vec,仅能表达一种含义(词向量是固定的)
- ELMo生成的词向量利用了上下文的信息,根据下游任务,能够通过权值来调整词向量以适应不同任务