数据结构python版（八）图及算法

1、图的基本概念和相关术语
顶点Vertex:顶点具有名称标识key，也可以携带数据项payload
边edge：作为两个顶点之间的关系表示，边连接两个顶点，边可以是无向或者有向的，相应的图称为无向图和有向图
权重weight：为了表达一个顶点到另一个顶点的代价，可以给边赋权。例如公交网络中两个站点的距离，时间和票价。
一个图可以定义为顶点和边的集合，G=(V,E)，V是顶点的集合，E是边的集合，E中的每条边e=(v,w)，v,w都是V中的顶点。
路径Path：图中的路径是由边依次连接起来的顶点序列，无权路径的长度为边的数量，带权路径的长度为所有边权重的和。
圈Cycle：圈是首尾顶点相同的路径。如果有向图中不存在任何一个圈则称作有向无圈图DAG。
树结构是一种特殊的DAG。

2、图抽象数据类型
(1)图的基本操作
Graph()：创建空的图
addVertex(vert)：将顶点vert加入图中
addEdge(fromVert,toVert)：添加有向边
addEdge(fromVert,toVert,weight)：添加带权的有向边
getVertex(vKey)：查找名称为vKey的顶点
getVertices():返回图中所有顶点的列表
in:按照vert in garph的语句形式，返回顶点是否存在图中。
(2)邻接矩阵方法实现图
矩阵的每行和列都代表图中的顶点。如果两个顶点之间有边连接，设定行列式值。其中无权边用0，1标注，有权边用权重值保存。

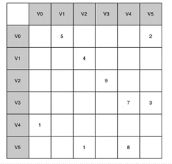
邻接矩阵的优点是简单，但如果图的边数比较少则效率低下，成为了稀疏矩阵。

(3)邻接列表
维护一个包含所有顶点的主列表。主列表中的每个顶点，再关联一个与自身有边边界的所有顶点的列表。
很容易获得顶点所连接的所有顶点以及连接边的信息，存储空间效率高。

(4)图的实现
首先实现顶点Vertex类

class Vertex:
    def __init__(self,key):
        self.id=key
        self.connectedTo={}
    def addNeighbor(self,nbr,weight=0):
        self.connectedTo[nbr]=weight
    def __str__(self):
        return str(self.id)+'connectedTo:'\
       +srt([x.id for x in self.connectedTo])
    def getConnections(self):
        return self.connectedTo.keys()
    def getId(self):
        return self.id
    def getWeight(self,nbr):
        return self.connectedTo[nbr]
class Graph:
    def __init__(self):
        self.verList={}
        self.numVertices=0
    def addVertex(self,key):
        self.numVertices+=1
        newVertex=Vertex(key)
        self.verList[key]=newVertex
        return newVertex
    def getVertex(self,n):
        if n in self.verList:
            return self.vertList[n]
        else:
            return None
    def __contains__(self,n):
        return n in self.verList
    def addEdge(self,f,t,cost=0):
        if f not in self.vertList:
            nv=self.addVertex(f)
        if t not in self.vertList():
            nv=self.addVertex(t)
        self.vertList[f].addNeighbor(\
                 self.verList[t],cost)
    def getVertices(self):
        return self.vertList.keys()
    def __iter__(self):
        return iter(self.verList.values())  

3、图的应用：词梯问题
从一个单词演变成另一个单词，其中过程可以经过多少中间单词。其中要求是相邻两个单词之间的差异只能是1个字母。
解决步骤如下：
(1)将所有可能的单词之间的演变关系表达为图：将单词作为顶点的标识key，如果两个单词之间仅相差一个字母，就在它们之间设一条边。
以四个字母的单词表为例：
创建大量的桶，每个桶可以存放若干单词，桶标记是去掉一个字母，通配符“_”占空的单词。然后将所有匹配标记的单词都放在这个桶里，再在同一个桶的单词之间建立边即可。如下图所示

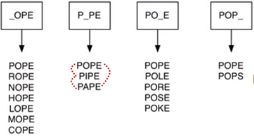
也就是说先把所有可能的相似组合列举，再遍历字母表去分组。

def buildGraph(wordFile):
    d={}
    g=Graph()
    wfile=open(wordFile,'r')#一行一个单词
    for line in wfile:
        word=line[:-1]
        for i in range(len(word)):#对每个单词都设4个桶
            bucket=word[:i]+'_'+word[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket]=[word]
    for bucket in d.keys():#对一个桶里的所有单词建立边
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word !=word2:
                    g.addEdge(word1,word2)
    return g  

(2)采用广度优先搜索BFS来搜寻从开始单词到结束单词之间的所有有效路径。

(a)广度优先搜索算法是搜索图的最简单算法之一。给定图G以及开始搜索的起始顶点s，BFS搜索所有从s可到达顶点的边而且在到达更远的距离k+1的顶点之前，BFS会找到全部距离为k的顶点。
可以类比以s为根构建一棵树的过程，从顶部向下逐步增加层次。广度优先搜索能保证在增加层次之前添加了所有兄弟节点到树中。

(b)为了跟踪顶点的加入过程，避免重复顶点，要为顶点加入三个属性：
距离distance：从起始顶点到此顶点的路径长度
前驱顶点predecessor：可反向追溯到起点.
颜色：标识了此顶点是尚未发现(白色)，已经发现（灰色）、还是已经完成探索（黑色）。

©还需要用一个队列Queue来对已发现的顶点进行排列，决定下一个要探索的顶点(队首顶点)。

(d)算法过程：
从起始顶点s开始，作为刚发现的顶点，标注为灰色，距离为0，前驱为None，加入队列，接下来是个循环迭代的过程。
从队首取出一个顶点作为当前顶点，遍历所有当前顶点的邻接顶点，如果是尚未发现的白色顶点，则将其颜色改为灰色（已发现），距离增加1，前驱顶点设置为当前顶点，加入到队列中。
遍历完成后，将当前顶点设置为黑色（已探索过），循环回到Queue的队首取当前顶点。

(e)代码如下：

def bfs(g,start):
    start.setDiatance(0)
    start.setPred(None)
    vertQueue=Queue()
    vertQueue.enqueue(start)
    while (wertQueue.size()>0):
        currentVert=vertQueue.dequeue()
        for nbr in\
            currentVert.getConnections():
            if (nbr.getColor()=='white'):
                nbr.setColor('gray')
                nbr.setDistance(1+\
                 currentVert.getDistance())
                nbr.setPred(currentVert)
                vertQueue.enqueue(nbr)
        currentVert.setColor('black')

算法分析:
主题是两个循环嵌套，while循环是对每个顶点访问一次，是O(|v|)。
而嵌套在while 中的for，由于每条边只有再其起始顶点u出队的时候才会被检查一次，而每个顶点最多出队一次，所以边最多被检查1次，一共是O(|E|)。
综合起来BFS的时间复杂度为O(|v|+|E|)
(3)选择其中最快到达目标单词的路径。
可以定义回溯函数来确定s到任何单词顶点的最短词梯。

def traverse(y):
    x=y
    while (x.getPred()):
        print(x.getId())
        x=x.getPred()
    print(x.getId())
wordgraph=buildGraph("fourletterwords.txt")
bfs(wordgraph,wordgraph.getVertex('FOOL'))
traverse(wordgraph.getVertex('SAGE'))

回溯过程是O(|v|)，创建单词关系图的时间最多为O(|v|**2)

5、图的应用：骑士周游问题
(1)问题介绍
在一个国际棋盘上，一个棋子马按照马走日的规则，从一个格子出发，要走遍所有棋盘恰好一次，把这样的走棋序列成为周游。

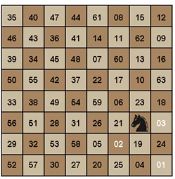
(2)问题分析
采用图搜索算法是解决该问题最容易理解和编程的方案之一。

(a)首先将合法走棋次序表示为一个图：
将棋盘格作为顶点，按照马走日的规则的走棋步骤作为连接边。建立每一个棋盘格的所有走起步骤能够到达的棋盘格关系图

def genLegalMoves(x,y,bdSize):
    newmoves=[]
    moveOffsets=[(-1,-2),(-1,2),(-2,-1),(-2,1),(1,-2),(1,2),(2,-1),(2,1)]
    for i in moveOffsets:
        newX=x+i[0]
        newY=y+i[1]
        if legalCoord(newX,bdSize) and\
           legalCoord(newY,bdSize):
            newMoves.append((newX,newY))
    return newMoves
def legalCoord(x,bdSize):
    if x>=0 and x<bdSize:
        return True
    else:
        return False
#构建走棋关系图
def knightGraph(bdSize):
    ktGraph=Graph()
    for row in range(bdSize):#遍历格子
        for col in range(bdSize):
            nodeId=posToNodeId(row,col,\
                                 bdSize)
            newPositions=genLegalMoves(row,\
                                  col,bdSize)
            for e in newPositions:#判断每个位置
                nid=posToNodeId(e[0],e[1],\
                                     bdSize)
                ktGraph.addEdge(nodeId,nid)
    return ktGraph
def psoToNode(row,col,bdSize):
    return row*bdSize+col

(b)采用搜索算法搜寻一个长度为（行*列-1）的路径，路径上包含每个顶点恰一次。
采用深度优先搜索(因为只要找到一条路就可以)

(3)深度优先搜索
深度优先搜索(Depth First Search)是沿着树的单支尽量深入向下搜索。如果到无法继续的程度还未找到问题的解，就回溯到上一层搜索下一支。
分为两种，一种用于解决骑士周游问题，其特点是每个顶点仅访问一次。另一个DFS算法更为通用，允许顶点被重复访问，可作为其它图算法的基础。
深度优先搜索解决骑士周游问题的关键思路：
如果沿着单支深入搜索到无法继续时路径长度还没有达到预定值(8*8棋盘为63)，那么就清除颜色标记，返回到上一层，换一个分支继续深入搜索。
这里需要引入一个栈来记录路径并返回实施上一层的回溯操作。

def knightTour(n.path,u,limit):
#n是搜索层次，path是路径，u是当前顶点，limit是搜索总深度。
#该函数是一个递归函数
    u.setColor('gray')
    path.append(u)
    if n<limit:
        nbrList=list(u.getConnections())
        i=0
        done=False
        while i <len(nbrList) and not done:
            if nbrList[i].getColor=='white':
            #选择白色的未经过的顶点深入
                done=knightTour(n+1,path,\
                         nbrList[i],limit)
            i=i+1
        if not done:
            path.pop()
            u.setColor('white')
    else:
        done=True
    return done

(4)代码分析和改进
该算法的性能高度依赖于棋盘的大小，55时要1.5s，88要半个小时。其复杂度是O(k**n)
可以对nbrList进行巧妙构造，以特定的方式排列顶点访问次序，可以使8*8棋盘的周游路径搜索时间降到秒级。
新的算法中，将u的合法移动目标棋盘格排序为：具有最少合法移动目标的格子优先搜索

def orderByAvail(n):
    resList=[]
    for v in n.getConnections():
        if v.getColor=='white':
            c=0
            for w in v.getConnections():
                if w.getColor()=='white':
                    c+=1
            resList.append((c,v))
    resList.sort(key=lambda x:x[0])
    return [y[1] for y in resList]

该算法采用先验的知识来改进算法性能，这种做法称为启发式规则。
启发式规则常用在人工智能领域；可以有效地减少搜索范围，更快的达到目标。
例如棋类程序算法会预先存入棋谱，布阵口诀等，能够在最短时间内从海量的棋局落子点搜索树中定位最佳落子。

6、通用的深度优先算法
一般的深度优先搜索目标是在图上进行尽量深的搜索，连接尽量多的顶点，必要时可以进行分支（一次性无法包括所有顶点）。有时候深度优先搜索会创建多棵树，称为深度优先森林。
深度优先搜索同样要用到顶点的前驱属性，来构建树或森林。另外要设置发现时间和结束时间的属性，前者是在第几步访问了这个顶点，后者是在第几步完成了此顶点探索。
为了实现DFS算法，Vertex中要增加Discovery及Finish。图Graph要增加成员time用于记录算法执行的步骤数目。

from pythonds.garphs import Graph
class DFSGraph(Graph):
    def __init__(self):
        super().__init__()
        self.time=0
    def dfs(self):#深度优先
    #self是指向类的实体化
        for aVertex in self:
            aVertex.setColor('white')#颜色初始化
            aVertex.setPred(-1)
        for aVertex in self:#如果有未包括的顶点则建立森林
            if aVertex.getColor=='white'
                self.dfvisit(aVertex)#调用一次创建一棵树
    def dfsvisit(self,startVertex):
    #startVertex是开始搜索的根顶点
        startVertex.setColor('gray')
        self.time+=1#算法步数
        startVertex.setDiscovery(set.time)
        for nextVertex in startVertex.\
                         getConnections():
            if nextVertex.getColor==:
                nextVertex.setPred(\
                    startVertex)
                self.dfsvisit(nextVertex)
                #深度优先递归访问
        startVertex.setColor('black')
        self.time+=1
        startVertex.setFinish(self.time)    

DFS构建的树，其顶点的发现时间和结束时间的属性，具有类似括号的性质。即一个顶点的发现时间总小于所有子顶点的发现时间，而结束时间则大于所有子顶点结束时间，比子顶点更早被发现，更晚被探索结束。

dfs函数中有两个循环，每个都是|v|次，所以是O(|v|)
而dfsvisit函数中的循环则是对当前顶点所连接的顶点进行，而且仅有在顶点为白色的情况下才进行递归调用，所以对每条边来说只会运行一次，所以是O(|E|)
因此总复杂速度是O(|E|+|v|)。

7、图的应用：拓扑排序
(1)拓扑排序简介
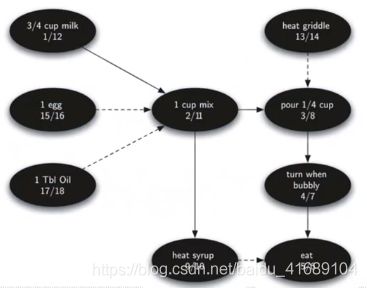
生活中很多问题都可以转化为图，利用图算法解决，例如早餐吃煎饼的过程，以动作为顶点，以先后次序为有向边。

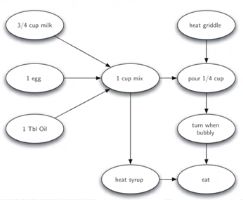
这时就需要从工作流程图来得到工作次序排列，这个过程就称为拓扑排序。
拓扑排序处理一个有向无圈图DAG,输出顶点的线性序列，使得两个顶点v,w，如果G中有(v,w)边，在线性序列中v就出现在w之前。
拓扑排序广泛应用于依赖事件的排期上，还可以用在项目管理、数据库查询优化和矩阵乘法的次序优化上。
(2)算法流程
可以用DFS实现
将工作流程建立为图，工作项是节点，依赖关系是有向边。
工作流程图一定是个DAG图，否则工作之间会形成循环依赖。
对DAG图调用DFS算法，以得到每个顶点的结束时间。
按照每个顶点的结束时间从大到小排序输出这个次序下的顶点列表。

8、图的应用：强连通分支
(1)背景介绍
互联网相关的非常巨大图。由主机通过网线连接而形成的图；以及由网页通过超链接连接而形成的图。
先看网页形成的图，以网页(URI作为ID)为顶点，网页内包含的超链接作为边，可以转换为一个有向图。
可以猜想，Web的底层结构可能存在某些同类网站的聚集。在图中发现高聚集节点群的算法，即寻找强连通分支Strongly Connected Components算法。
(2)强连通分支
定义为图G的一个子集C，C中的任意两个顶点w,v之间都有路径来回，即(v,w)(w,v)都是路径，而且C是具有这样性质的最大子集。
通过强连通分支可以对图的顶点进行分类，并对图进行简化。
(3)转置Transposition
一个有向图G的转置GT定义为将图G的所有边的顶点交换次序，如将边(v,w)转换为边(w,v)，即交换边的方向。
可以观察到图和转置图在强连通分支的数量和划分上，是相同的。
(4)kosaraju算法
首先对图G调用DFS算法，为每个顶点计算结束时间。
然后对图G进行转置
再对转置调用DFS算法，但在dfs函数中，对每个顶点的搜索循环里，要以顶点的结束时间的倒序来搜索(之前是任意点进行搜素)。
最后，深度优先森林中的每一棵树就是一个强连通分支。

9、图的应用：最短路径
(1)背景
当PC上的浏览器向服务器请求一个网页时，请求信息需要：
先通过本地局域网，有路由器A发送到Internet，请求信息沿着Internet中的众多路由器传播，最后到达服务器本地局域网所属的路由器B，从而传给路由器。如下图所示

上图中，标注Internet的云状结构实际上是一个由路由器连接成的网络。这些路由器各自独立而又协同工作，负责将信息从Internet的一端传送到另一端。
我们可以通过traceroute命令来跟踪信息传颂的路径。eg:输入
traceoute www.lib.buaa.edu.cn
可以追踪从本机到图书馆服务器的一条路由器路径。
由于网络状况会影响，路径选择算法，路径可能不同。
将互联网的路由器体系表示为一个带权边的图，路由器作为顶点，路由器之间的网络连接作为边。权重可以包括网络连接的速度，网络负载程度，分时段优先级等因素。这里我们一般把所有影响因素合成成为单一的权重。

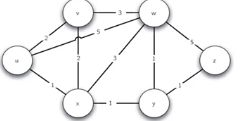
(2)最短路径问题
在带权图上寻找最短路径，与BFS算法解决词梯问题相似，只是在边上增加了权重。
解决带权图最短路径的经典算法是Dijkstra算法。这是一个迭代算法，得出从一个顶点到其余所有顶点的最短路径，很接近于广度优先搜索算法的结果。
具体实现上，在顶点Vertex类中的成员dist用于记录从开始顶点到本顶点的最短带权路径长度，算法对图中的每个顶点迭代一次。
(3)Dijkstra算法
顶点的访问次序由一个优先队列来控制，队列中作为优先级的是顶点的dist属性
最初，只有开始顶点dist设为零，而其它所有顶点dist设为sys.maxsize(最大整数)，全部加入优先队列。
随着队列中每个最低dist顶点率先出队，并计算它与邻接顶点的权重，这会引起其它顶点dist的减小和修改，引起堆重排，并根据更新后的dist优先级再依次出队，直到队列为空。

该算法只是定义了遍历的方法，即从dist最小的开始，但总体跟BFS没有区别，只是该算法不一定会先遍历完一个点的全部邻接顶点再去开始下一层。
距离的更新采用最小原则，如果新的距离比原来距离大就不更新。

(4)代码实现

from pythonds.graphs import PriorityQueue\
                          ,Vertex,Graph
import sys
def dijkstra(aGraph,start):
    pq=PriorityQueue()
    for v in aGraph:
        v.setDistance(sys.maxsize)
        v.setPred(None)
    start.setDistance(0)
    pq.buildHeap([(v.getDistance(),v) \
      for v in aGraph])#对所有顶点建堆，形成优先队列
    while not pq.isEmpty:
        currentVert=pq.delMin()#优先队列出列
        for nextVert in currentVert.\
                   getConnections():
            newDist=currentVert+\
                        currentVert.\
                     getWeight(nextVert)
            if newDist<\
                 nextVert.getDistance():
           #修改出队顶点邻接顶点的dist，并逐个重新排队
                newVert.setDistance=\
                                newDist
                newVert.setPred=\
                           currentVert 
                pq.decreaseKey(nextVert,\
                                  newDist)

(5)算法分析
需要注意的是,Dijkstra算法只能处理大于0的权重，否则算法会陷入无限循环。
Dijkstra算法需要具备整个图的数据，而对于Internet的路由器来说，显然无法将整个Internet所有路由器及其连接信息保存在本地，这不仅是数据量的变化，还因为Internet处于不断的动态变化中，这使得保存是不现实的。
建堆的过程复杂度是O(|V|)
其次，每个顶点仅出队1次，每次delMin花费O(log|V|)，一共就是O(|V|log|V|).
另外每个边关联到的顶点会做一次decreaseKey操作，是O(log|V|),一共是O(|E|log|V|)
因此算法的数量级是O((|V|+|E|)log|V|)

10、图的应用：最小生成树
(1)背景
信息广播问题：网游需要让所有玩家获知其他玩家所在位置，收音机则需要让所有听众获取直播的音频数据。
单播解法：采用上个问题的解法是可行的，但是这会使每个路由器发送许多重复的消息，会产生许多额外流量。
洪水解法：他的暴力解法是将每条消息在路由器间散布出去，所有的路由器都将收到的消息转发给自己相邻的路由器和收听者。但这样会使得很多路由器和收听者不断收到相同重复的消息。所以该解法一般会给每条消息附加一个生命值(TTL:Time To Live)，初始设置为从消息源到最远收听者的距离；每个路由器收到一条消息，如果其TTL值大于零，则将TTL减少1，再转发出去，如果TTL等于0，就直接抛弃掉这个消息。但是这样的话比前述的单播方法所产生的流量还要大。

(2)最小权重生成树
信息广播问题的最优解法依赖于路由器关系图上选取具有最小权重的生成树(生成树指拥有图中所有顶点和最少数量的边，以保持联通的子图)。
图G(V,E)的最小生成树T，定义为包含所有顶点V以及E的无圈子集，并且边权重之和最小。
有了最小权重生成树之后，信息广播就只需要从A开始，沿着树的路径层次向下传播，就可以达到每个路由器只需要处理1次消息，同时总费用最小。

(3)Prim算法
属于贪心算法，即每步都沿着最小权重的边向前搜索。
构造最小生成树的思路很简单，如果T还不是生成树，则反复去做，找到一条最小权重的可以安全添加的边，将边添加到树T。
可以安全添加的边，定义为一端顶点在树中，另一端不在树中的边，以保持边的无圈特性。
(4)代码实现

from pythonds.graphs import \
                PriorityQueue,Graph,Vertex
import sys
def prim(G,start):
    pq=PriorityQueue()
    for v in G:
        v.setDistance(sys.maxsize)
        v.setPred(None)
    start.setDistance(0)
    pq.buildHeap([(v.getDistance(),v) for v in G])
    while not pq.isEmpty():
        currentVert =pq.delMin()
        for nextVert in currentVert.getConnections():
        #取跟现有节点相邻的全部节点
            newCost=currentVert.getWeight(nextVert)
            if nextVert in pq and newCost< nextVert.getDistance():
            #nextVert in pq要判断它是否是一条可以安全添加的边
                nextVert.setPred(currentVert) 
                nextVert.setDistance(newCost)
                pq.decreaseKey(nextVert,newCost)#把它添加到优先队列前面去