风控模型指标详解

目录：

• 1.P-R曲线
• 2.ROC,AUC
  • P-R曲线和ROC曲线的区别
• 3.WOE.IV值
• 4.K-S值
• KS曲线与ROC曲线的区别
• 5.PSI,CSI
  • PSI
  • CSI
  • PSI和CSI的区别
• 6.Lift曲线

1.P-R曲线

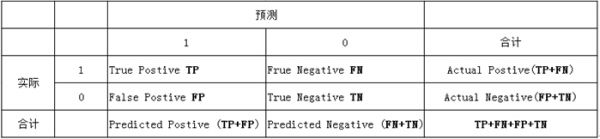
 　首先，明确两个概念，精确率§和召回率®。下表中，1代表正例，0代表负例。

$$P=\frac{TP}{P}=\frac{TP}{TP+FP}$$
$$R=\frac{TP}{R}=\frac{TP}{TP+FN}$$

 　精确率是指分类正确的正样本个数占分类器判定为正样本个数的比例。它表示的是预测为正的样本中有多少是真正的正样本。
召回率是指分类正确的样本个数占真正的正样本个数的比例，它表示的是样本中的正例有多少被预测正确了。这里可以参看西瓜书，里面好瓜坏瓜的例子，比较容易理解。

 　Precision和Recall是既矛盾又统一的两个指标，为了提高Precision,分类器需要尽量在“更有把握”时才把样本预测为正样本，但此时往往会因为过于保守而漏掉很多“没有把握”的正样本，导致Recall很低。

 　接下来说回P-R曲线，横轴是召回率R,纵轴是精确率P。对于P-R曲线上的一点，表示在某一阈值下，模型将大于该阈值的结果判定为正样本，小于该阈值的结果判定为负样本，此时返回结果对应的P和R。一般的P-R曲线如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tOhuUphD-1575456885844)(./image/PR曲线.jpg)]
注意，只用某个点对应的精确率和召回率无法全面衡量模型性能。

2.ROC,AUC

 　介绍ROC之前，先看几个指标，假阳率(FPR)和真阳率(TPR)。

$$FPR=\frac{FP}{N}=\frac{FP}{FP+TN}$$
$$TPR=\frac{TP}{P}=\frac{TP}{TP+FN}$$

 　P是真实的正样本数量，N是真实的负样本数量。TP是P个正样本中被分类器预测为正样本的个数，FP是N个负样本中被分类器预测为正样本的个数。
 　可以这样记这两个公式，以TPR为例，分子就是TP,因为T意味着P(正)分类正确，所以分母为P(正类)。正类有两种，一种是预测为正类且预测正确(TP)，一种是预测为负类但是预测错误(FN)。FPR同理，只是分母为N而已。
ROC曲线通过不断移动分类器的“截断点”来生成曲线上的一组关键点。
具体介绍见https://zhuanlan.zhihu.com/p/60218684(不想写了。。。)

P-R曲线和ROC曲线的区别

 　当正负样本的分布发生变化时，ROC曲线形状基本保持不变，P-R曲线会发生剧烈变化。但是，在正负样本分布极不均匀的情况下，P-R曲线比ROC曲线更能有效反应分类的好坏。

3.WOE.IV值

 　WOE和IV主要用来判断变量的预测强度，比如判断用户收入对用户是否会发生逾期的预测强度。因此，两个值的使用主要是在有监督的分类问题中，具体可以细化到如下方面：

指导变量离散化。在建模过程中，时常需要对连续变量进行离散化处理，如将年龄进行分段。但是变量不同的离散化结果（如：年龄分为［0-20］还是［0-15］）会对模型产生不同影响。因此，可以根据指标所反应的预测强度，调整变量离散化结果。（对一些取值很多的分类变量，在需要时也可以对其进行再分组，实现降维。）

变量筛选。我们需要选取比较重要的变量加入模型，预测强度可以作为我们判断变量是否重要的一个依据。

 　WOE的全称是“Weight of Evidence”，即证据权重。WOE是对原始自变量的一种编码形式。要对一个变量进行WOE编码，需要首先把这个变量进行分组处理（也叫离散化、分箱等等，说的都是一个意思）。下面以german credit数据来解释WOE及后面的IV值，选取savings这个分类字段进行相应解释，此字段共有5个取值，每个取值代表一个分组，每个分组中好坏样本数如下，其中0代表未违约，1代表违约：

	0(未违约)	1(违约)	总计
A61	386	217	603
A62	69	34	103
A63	52	11	63
A64	42	6	48
A65	151	32	183
总计	700	300	1000

WOE公式如下：
$$WO{E}_i=ln\frac{P(y_i)}{P(n_i)}=ln\frac{\frac{y_i}{y}}{\frac{n_i}{n}}$$
P(yi)代表第i组中，违约样本占所有违约样本的比例；
P(ni)代表第i组中，未违约样本占所有未违约样本比例；
y：所有违约样本数；
n：所有未违约样本数。
 　经过变换，上述式子可以变为
$WO{E}_i=ln\frac{\frac{y_i}{n_i}}{\frac{y}{n}}$

	0(未违约)	1(违约)	总计	WOE
A61	386	217	603	0.271
A62	69	34	103	0.14
A63	52	11	63	-0.706
A64	42	6	48	-1.099
A65	151	32	183	-0.704
总计	700	300	1000

 　以变量取A61时为例，对应的woe＝ln（（217/300）／（386／700））。 即每一组中坏样本比例除以好样本比例。在大于0部分（说明坏样本比例大于好样本比例），WOE越大，说明坏样本比例比好样本比例大得越多，即分组中存在坏样本的可能性越大；小于0部分(坏样本比例小于好样本比例），WOE越小，说明坏样本比例比好样本比例小得越多，即分组中存在好样本的可能性越大)。总结下来，WOE越小好样本可能性越大。

 　但是，WOE没有考虑分组中样本占整体样本的比例，如果一个分组的WOE值很高，但是样本数占整体样本数很低，则对变量整体预测的能力会下降。因此，我们还需要计算IV值。
 　IV值考虑了分组中样本占整体样本的比例，相当于WOE的加权求和。具体计算公式如下：

$$I{V}_i=(P(y_i)-P(n_i))\ast WO{E}_i=(\frac{y_i}{y}-\frac{n_i}{n})ln\frac{\frac{y_i}{y}}{\frac{n_i}{n}}$$

	0(未违约)	1(违约)	总计	WOE	IV
A61	386	217	603	0.271	0.047
A62	69	34	103	0.14	0.002
A63	52	11	63	-0.706	0.027
A64	42	6	48	-1.099	0.044
A65	151	32	183	-0.704	0.077
总计	700	300	1000		0.197

 　有了一个变量各分组的IV值，我们就可以计算整个变量的IV值，方法很简单，就是把各分组的IV相加：

$$IV=\sum _{i=1}^{n}I{V}_i$$

其中，n为变量分组个数。

 　IV值可以用来衡量自变量的预测能力。类似的指标还有信息增益、基尼系数等等。

4.K-S值

 　KS曲线是用来衡量分类型模型准确度的工具。KS曲线与ROC曲线非常的类似。KS曲线是两条线，其横轴是阈值，纵轴是TPR与FPR。两条曲线之间之间相距最远的地方对应的阈值，就是最能划分模型的阈值。

KS的计算步骤如下：

1. 计算每个评分区间的好坏账户数。
2. 计算每个评分区间的累计好账户数占总好账户数比率(good%)和累计坏账户数占总坏账户数比率(bad%)。
3. 计算每个评分区间累计坏账户占比与累计好账户占比差的绝对值（累计good%-累计bad%），然后对这些绝对值取最大值即得此评分卡的K-S值。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8nWcFOAe-1575456885845)(./image/K-S值.png)]
 　K-S指标衡量的是好坏样本累计分部之间的差值。
好坏样本累计差异越大，KS指标越大，那么模型的风险区分能力越强。

KS曲线与ROC曲线的区别

 　KS曲线就是把ROC曲线由原先的一条曲线拆解成了两条曲线。原先ROC的横轴与纵轴都在KS中变成了纵轴，而横轴变成了不同的阈值。

5.PSI,CSI

PSI

 　PSI又叫作群体稳定性指标，常用来筛选特征变量、评估模型稳定性。公式如下：
$$PSI=\sum _{i=1}^n(A_i-E_i)\ast ln(A_i/E_i)$$

$A_i$表示实际占比，$E_i$表示预期占比。

 　通常，以训练样本作为预期分布占比，验证样本作为实际分布占比。

Score	A%	E%	A-E	A/E	PSI
0-200	20%	10%	10%	0.875	0.0013
200-300	30%	20%	10%	0.8000	0.0045
300+	50%	70%	-20%	1.1111	0.00111
总计					0.0069

 　PSI数值越小，两个分布之间的差异就越小，代表越稳定。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-i2lb7dzw-1575456885846)(./image/PSI.jpg)]
 　模型部署上线后，通常用PSI曲线报表观察模型的稳定性。通过保证入模变量稳定性来进行变量监控，保证模型分数稳定性来进行模型监控。

根据建模经验，给出一些建议：

1. 实际评估需要分不同粒度：时间粒度（按月、按样本集）、订单层次（放贷层、申请层）、人群（若没有分群建模，可忽略）。
2. 先在放贷样本上计算PSI，剔除不稳定的特征；再对申请样本抽样（可能数据太大），计算PSI再次筛选。之前犯的错误就是只在放贷样本上评估，后来在全量申请订单上评估时发现并不稳定，导致返工。
3. 时间窗尽可能至今为止，有可能建模时间窗稳定，但近期时间窗出现
4. PSI只是一个宏观的指标，建议先看变量数据分布（EDD），看分位数跨时间变化来检验数据质量。我们无法得知PSI上升时，数据分布是左偏还是右偏。因此，建议把PSI计算细节也予以保留，便于在模型不稳定时，第一时间排查问题。
   转自https://zhuanlan.zhihu.com/p/79682292

---

CSI

 　CSI又叫作特征稳定性指标，能帮助理解入模特征变量对模型分数波动的影响，以及背后的客群分布偏移原因。这对风控模型不稳定时追溯定位原因具有重要意义。
$$CSI=\sum _{i=1}^n(Distr\_A_i-Distr\_E_i)\ast partial\_Scor{e}_i$$

$Distr\_A_i$表示实际占比，$Distr\_E_i$表示预期占比。
关于CSI，注意以下几点:

1. 符号为正，说明当前样本相对于开发样本往高分段偏移；符号为负，说明说明当前样本相对于开发样本往低分段偏移。
2. CSI绝对值数值越大，特征稳定性越差。
3. 不同变量间的CSI没有可比性。

---

PSI和CSI的区别

1. 群体稳定性报告（Population Stability Report）是用模型分数层（score）来评估当前样本与开发样本之间的分布差异。目前业内有可以统一参考来判断稳定性的阈值标准。
2. 特征稳定性报告（Characteristic Stability Report）是从入模特征层（characteristic）来分析当前样本与开发样本之间的分数差异，以及对最终模型分数的影响。目前没有统一参考来判断稳定性的阈值标准。

风控模型不稳定时的排查方向
 　当通过PSI指标发现模型不稳定时，我们该如何去排查原因？引起模型不稳定的因素是多种多样的，主要包括：

申贷客群变化：获客渠道一般决定了客群质量，我们只是从客群的有限特征维度来大致判断是否变化，但这只是有偏判断，因为无法完全获知用户画像。当然，在获客阶段也会做前置风控，预先筛选流量，以及保证客群的稳定。
数据源不稳定：先从CSI指标观察入模特征的分数漂移，对于影响较大和偏移较大的变量予以重点关注。再从数据源上确认采集是否可靠，比如数据服务商是否正常提供、接口是否正常工作、网关数据传输过程是否正常等。
特征逻辑有误：在模型上线时，特征逻辑可能没有确认清楚，导致上线后出现意想不到的问题。因此，需要将入模特征的逻辑再次予以Review。
其他相关原因：模型监控报表是否正确计算？线上依赖于离线T+1产出的数据是否正常调度？特征缺失值处理逻辑？
转自https://zhuanlan.zhihu.com/p/86559671

6.Lift曲线

 　Lift是评估一个预测模型是否有效的一个度量；它衡量的是一个模型（或规则）对目标中“响应”的预测能力优于随机选择的倍数，以1为界线，大于1的Lift表示该模型或规则比随机选择捕捉了更多的“响应”，等于1的Lift表示该模型的表现独立于随机选择，小于1则表示该模型或规则比随机选择捕捉了更少的“响应”。Lift计算公式：
$$Lift=\frac{\frac{TP}{TP+FP}}{\frac{TP+FN}{TP+FP+TN+FN}}=\frac{查准率}{正例占比}$$

 　Lift指标可以这样理解：在不使用模型的情况下，我们用先验概率估计正例的比例，即上式分母部分，以此作为正例的命中率；利用模型后，我们不需要从整个样本中来挑选正例，只需要从我们预测为正例的那个样本的子集{TP+FP}中挑选正例，这时正例的命中率为查准率 ，后者除以前者即可得提升值Lift。
下表是一个提升表（Lift Table）的示例：

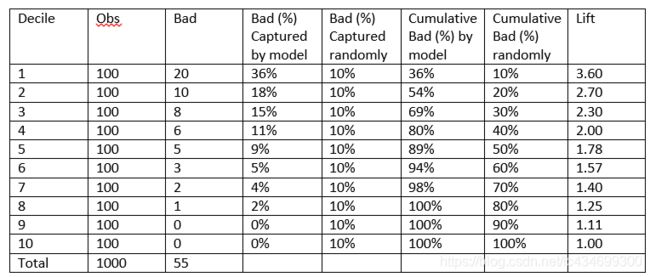
 　Decile表示分数段，Obs表示不使用评分卡，用随机选择方法覆盖到的坏客户占比，等价于该组观测数占总观测数的比例（分子分母同时乘以样本整体的坏账率）。Bad表示使用评分卡得到的坏客户占比。
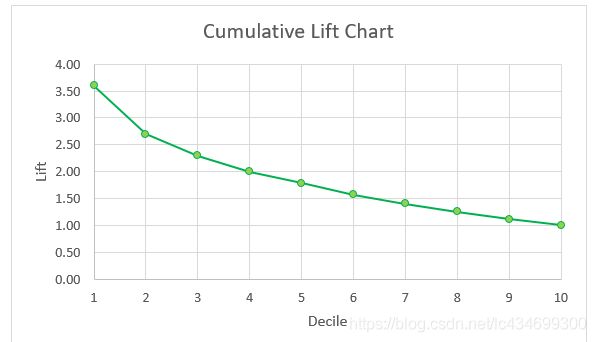
以分数段为横轴，以提升度为纵轴，可绘制出累计提升图，示例如下：

 　Lift曲线的右半部分应该尽量陡峭，因为越陡峭说明低分段中的Bad占比越大，模型的区分能力越好。

作者：Labryant 著作权归作者所有。转载请注明出处。