【学习笔记】【机器学习】第3章——线性模型

第3章 线性模型 53

3.1 基本形式 53

给定由 $d$ 个属性描述的示例 $\mathbf{x}=(x_1;x_2;\dots ;x_d)$ ，其中 $x_i$ 是 $\mathbf{x}$ 在第 $i$ 个属性上的取值，线性模型(linear model)试图学得一个通过属性得线性组合来进行预测的函数，即
$$f(\mathbf{x})=w_1{x}_1+w_1{x}_1+\cdot \cdot \cdot +w_d{x}_d+b，$$

一般用向量形式写成
$$f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b，$$

其中$\mathbf{w}=(w_1;w_2;\dots ;w_d)$。 $\mathbf{w}$ 和 $b$ 学得之后，模型就得以确定。
由于 $\mathbf{w}$ 直观表达了各属性在预测中的重要性，因此线性模型有很好的可解释性。

3.2 线性回归 53

线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记
$$f(x_i)=w{x}_i+b，使得f(x_i)\simeq y_i$$

均方误差最小化
$$\begin{array}{rl}(w^{\ast },b^{\ast })& =\underset{(w,b)}{\mathrm{argmin}}\sum _{i=1}^m(f(x_i)-y_i{)}^2\\ & =\underset{(w,b)}{\mathrm{argmin}}\sum _{i=1}^m(y_i-w{x}_i-b{)}^2\end{array}$$

均方误差有非常好的几何意义，它对应了常用的欧几里得距离或简称“欧氏距离”。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。
求解 $w$ 和 $b$ 使 $E_{(w,b)}={\sum }_{i=1}^m(y_i-w{x}_i-b{)}^2$最小化的过程，称为线性回归模型的最小二乘“参数估计”。将 $E_{(w,b)}$ 分别对 $w$ 和 $b$ 求导，得到
$$\begin{array}{rl}\frac{\partial E_{(w,b)}}{\partial w}& =\frac{\partial }{\partial w}\left[\sum _{i=1}^m{\left(y_i-w{x}_i-b\right)}^2\right]\\ & =\sum _{i=1}^m\frac{\partial }{\partial w}\left[{\left(y_i-w{x}_i-b\right)}^2\right]\\ & =\sum _{i=1}^m\left[2\cdot \left(y_i-w{x}_i-b\right)\cdot (-x_i)\right]\\ & =\sum _{i=1}^m\left[2\cdot \left(w{x}_i^2-y_i{x}_i+b{x}_i\right)\right]\\ & =2\cdot \left(w\sum _{i=1}^m{x}_i^2-\sum _{i=1}^m{y}_i{x}_i+b\sum _{i=1}^m{x}_i\right)\\ & =2\left(w\sum _{i=1}^m{x}_i^2-\sum _{i=1}^m\left(y_i-b\right)x_i\right)\end{array}$$

同理
$$\begin{array}{rl}\frac{\partial E_{(w,b)}}{\partial b}& =\frac{\partial }{\partial b}\left[\sum _{i=1}^m{\left(y_i-w{x}_i-b\right)}^2\right]\\ & =\sum _{i=1}^m\frac{\partial }{\partial b}\left[{\left(y_i-w{x}_i-b\right)}^2\right]\\ & =\sum _{i=1}^m\left[2\cdot \left(y_i-w{x}_i-b\right)\cdot (-1)\right]\\ & =\sum _{i=1}^m\left[2\cdot \left(b-y_i+w{x}_i\right)\right]\\ & =2\cdot \left[\sum _{i=1}^{m}b-\sum _{i=1}^m{y}_i+\sum _{i=1}^{m}w{x}_i\right]\\ & =2\left(mb-\sum _{i=1}^m\left(y_i-w{x}_i\right)\right)\end{array}$$

令上述两式分别为0，可得到 $w$ 和 $b$ 最优解的闭式解
$$\begin{array}{rl}0& =w\sum _{i=1}^m{x}_i^2-\sum _{i=1}^m(y_i-b)x_i\\ w\sum _{i=1}^m{x}_i^2& =\sum _{i=1}^m{y}_i{x}_i-\sum _{i=1}^{m}b{x}_i\\ w\sum _{i=1}^m{x}_i^2& =\sum _{i=1}^m{y}_i{x}_i-\sum _{i=1}^m(\bar{y}-w\bar{x})x_i\\ w\sum _{i=1}^m{x}_i^2& =\sum _{i=1}^m{y}_i{x}_i-\bar{y}\sum _{i=1}^m{x}_i+w\bar{x}\sum _{i=1}^m{x}_i\\ w(\sum _{i=1}^m{x}_i^2-\bar{x}\sum _{i=1}^m{x}_i)& =\sum _{i=1}^m{y}_i{x}_i-\bar{y}\sum _{i=1}^m{x}_i\\ w& =\frac{{\sum }_{i=1}^m{y}_i{x}_i-\bar{y}{\sum }_{i=1}^m{x}_i}{{\sum }_{i=1}^m{x}_i^2-\bar{x}{\sum }_{i=1}^m{x}_i}\\ w& =\frac{{\sum }_{i=1}^m{y}_i(x_i-\bar{x})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}\end{array}$$

同理
$$\begin{array}{rl}0& =mb-\sum _{i=1}^m\left(y_i-w{x}_i\right)\\ mb& =\sum _{i=1}^m\left(y_i-w{x}_i\right)\\ b& =\frac{1}{m}\sum _{i=1}^m\left(y_i-w{x}_i\right)\end{array}$$

更一般的情况是样本由 $d$ 个属性描述，称为“多元线性回归”。类似的，可以用最小二乘法来对 $\mathbf{w}$ 和 $b$ 进行估计。把 $\mathbf{w}$ 和 $b$ 吸收入向量形式$\hat{\mathbf{w}}=(\mathbf{w};b)$，把数据集 $D$ 表示为一个 $m\times (d+1)$ 大小的矩阵 $\mathbf{X}$
$$\mathbf{X}=\left(\begin{array}{ccccc}{x}_{11}& x_{12}& \cdots & x_{1d}& 1\\ x_{21}& x_{22}& \cdots & x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \cdots & x_{md}& 1\end{array}\right)=\left(\begin{array}{cc}{\mathbf{x}}_1^{\mathrm{T}}& 1\\ {\mathbf{x}}_2^{\mathrm{T}}& 1\\ ⋮& ⋮\\ {\mathbf{x}}_m^{\mathrm{T}}& 1\end{array}\right)$$

把标记写成向量形式 $\mathbf{y}=(y_1;y_2;\dots ;y_m)$，有
$$\begin{array}{rl}{\hat{\mathbf{w}}}^{\ast }& =\underset{\hat{\mathbf{w}}}{\mathrm{argmin}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}}{)}^{\mathrm{T}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}})\end{array}$$

令 $E_{\hat{\mathbf{w}}}=(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}}{)}^{\mathrm{T}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}})$，对 $\hat{\mathbf{w}}$ 求导得
$$\begin{array}{rl}\frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}& =\frac{\partial ({\mathbf{y}}^{\mathrm{T}}\mathbf{y}-{\mathbf{y}}^{\mathrm{T}}\mathbf{X}\hat{\mathbf{w}}-{\hat{\mathbf{w}}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{y}+{\hat{\mathbf{w}}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{X}\hat{\mathbf{w}})}{\partial \hat{\mathbf{w}}}\\ & =\frac{\partial {\mathbf{y}}^{\mathrm{T}}\mathbf{y}}{\partial \hat{\mathbf{w}}}-\frac{\partial {\mathbf{y}}^{\mathrm{T}}\mathbf{X}\hat{\mathbf{w}}}{\partial \hat{\mathbf{w}}}-\frac{\partial {\hat{\mathbf{w}}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{y}}{\partial \hat{\mathbf{w}}}+\frac{\partial {\hat{\mathbf{w}}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{X}\hat{\mathbf{w}}}{\partial \hat{\mathbf{w}}}\\ & =0-{\mathbf{X}}^{\mathrm{T}}\mathbf{y}-{\mathbf{X}}^{\mathrm{T}}\mathbf{y}+({\mathbf{X}}^{\mathrm{T}}\mathbf{X}+{\mathbf{X}}^{\mathrm{T}}\mathbf{X})\hat{\mathbf{w}}\\ & =2{\mathbf{X}}^{\mathrm{T}}(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y})\end{array}$$

令上式为零可得
$$\begin{array}{rl}{\hat{\mathbf{w}}}^{\ast }& =({\mathbf{X}}^{\mathrm{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{y}\end{array}$$

最终线性回归模型为
$$\begin{array}{rl}f(\widehat{{\mathbf{x}}_{\mathbf{i}}})& ={\widehat{{\mathbf{x}}_{\mathbf{i}}}}^{\mathrm{T}}({\mathbf{X}}^{\mathrm{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{y}\end{array}$$

简写为
$$y={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$

对数线性回归，实际上是在试图让 $e^{{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b}$ 逼近 $y$ 。形式上仍为线性回归，但实质上已是在求取输入空间到输出空间的非线性函数映射。

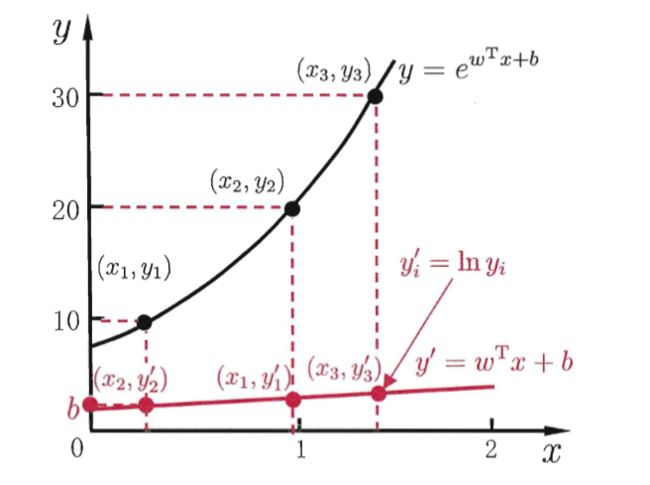
广义线性模型
$$y=g^{-1}({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b)$$

其中函数 $g(\cdot )$ 称为联系函数，对数线性回归是广义线性模型在 $g(\cdot )=ln(\cdot )$ 时的特例。

3.3 对数几率回归 57

对数几率函数是一种“Sigmoid函数”
$$y=\frac{1}{1+e^{-x}}$$

对数几率
$$\ln \frac{y}{1-y}$$

3.4 线性判别分析 60

线性判别分析（LDA）是一种经典的线性学习方法：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。

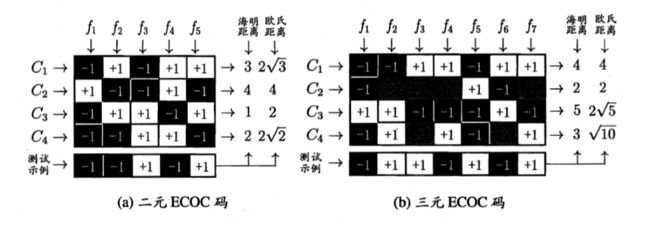
3.5 多分类学习 63

多分类通过ECOC编码进行拆分。

3.6 类别不平衡问题 66

类别不平衡是指分类任务中不同类别的训练样例差别很大的情况。
当正反例可能性相同时，若 $\frac{y}{1-y}>1$ 则 预测为正例；反之，令 $m^{+}$ 表示正例数目， $m^{-}$ 表示反例数目，若 $\frac{y}{1-y}>\frac{m^{+}}{m^{-}}$ 则 预测为正例。

再缩放
$$\frac{y^{\prime }}{1-y^{\prime }}=\frac{y}{1-y}\times \frac{m^{-}}{m^{+}}$$

欠采样：去除一些反例使得正、反例数目接近，然后再进行学习。
过采样：增加一些正例使得正、反例数目接近，然后再进行学习。
阈值移动：直接基于原始数据集进行学习，但在用训练好的分类器进行预测时，将再缩放嵌入到决策过程中。

习题 69