OpenCV(五)——超细节的Canny原理及算法实现
继上一章承诺,编写这一章。
原因呢,是这样,在实际项目中,用到canny很少,我总觉得它对于细节边缘过于详尽。
我们知道,opencv提供的算法库,内部核心算法是定死的,你只能通过调节参数来测试。
如果你不知道原理,估计这次调好了,下次又要花大半时间去。简直是无用功。
本着专研精神,还有也方便自己后续查阅,于是乎我就推出这一期的Canny算法。
啰嗦几句,其实要学好算法,看书是必不可少的,很多时候,度娘,必应,知乎啊等等,查不到你要的。
推荐一本好书《图像处理与计算机视觉算法及应用》(第2版)。
根据书本所述Canny的描述:
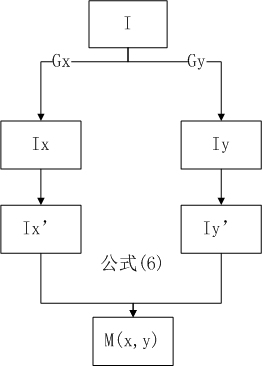
(1)读入要处理的图像I
(2)创建一个一维高斯掩模G用于对I进行卷积运算,这个高斯函数的标准偏差是传入边缘检测器的一个参数。
(3)在x和y方向上创建高斯函数的一阶导数作为一维掩模,分别称为Gx和Gy。s值和步骤(2)中使用的一样。
(4)沿着行利用G对图像I做卷积运算得到x分量图像Ix,沿着列利用G对图像I做卷积运算得到y分量图像Iy。
(5)利用Gx对Ix进行卷积运算得到Ix',即利用高斯函数的导数对I的x分量进行卷积,然后利用Gy对Iy进行卷积运算得到Iy'。
(6)结合x分量和y分量计算边缘响应的强度(即,是否希望在这一点看到结果)。每个像素(x,y)上的强度结果可以通过下式计算:
(7)非最大抑制。
(8)滞后双阈值化。
其中(1)~(6)的流程如下
(2)步骤代码:
一维高斯掩模:
double gauss(float x, float sigma)
{
float xx;
if(sigma == 0 ) return 0;
if(x == 0) return 1;
xx = (float)exp((double)((-x*x)/(2*sigma*sigma)));
return xx;
}调用代码:
Mat x_gauss; //x方向一维高斯掩模
Mat y_gauss = getGaussianKernel(11, sigma_);/y方向一维高斯掩模
transpose(y_gauss,x_gauss ); //转置(3)步骤代码:
一维偏导高斯掩模:
double dgauss(float x, float sigma)
{
float xx;
if(sigma == 0) return 0;
if(x == 0) return 0;
xx = (-x / (sigma * sigma)) * (float)exp((double)((-x*x)/(2*sigma*sigma)));
return xx;
}调用代码:
Mat dx_gauss; //x方向一阶偏导高斯掩模
Mat dy_gauss = getDerivGaussianKernel(11,sigma_);//y方向一阶偏导高斯掩模
transpose(dy_gauss,dx_gauss); //转置(4)步骤代码:
I图像分别和Gx和Gy卷积,生成Ix和Iy:
Mat x_mat, y_mat; //Ix Iy分量
filter2D(image, x_mat, -1, x_gauss); //卷积
filter2D(image, y_mat, -1, y_gauss); //卷积(5)步骤代码:
Ix和Iy,分别和Gx'和Gy'卷积,生成Ix'和Iy'。
filter2D(x_mat, x_mat, -1, dx_gauss);
filter2D(y_mat, y_mat, -1, dy_gauss);(6)步骤代码:
计算边缘响应,其中*20是为了提升灰度,否则图像处理过后太暗。
Mat dst = Mat::zeros(image.size(), CV_8UC1);
for(int i = 0; i < image.cols; i++)
{
for(int j = 0; j < image.rows; j++)
{
double s_value = sqrt(1.0 * x_mat.at(j,i) * x_mat.at(j,i)
+ 1.0 * y_mat.at(j,i) * y_mat.at(j,i)) * 20;
s_value = s_value >= 255 ? 255 : s_value;
dst.at(j,i) = s_value;
}
}
好了,前面6个步骤应该比较容易理解。然而(7)和(8)才是Canny算法的精髓。
(7)原理解析:
解析图我就参考了别人画的图了:
http://www.cnblogs.com/techyan1990/p/7291771.html
什么意思呢?
根据步骤(5)得到的两幅Ix'和Iy',相同位置点的像素的比例就是tan,也就是角度正切值。
图像梯度分量:分为0,45,90,135。
如他微博中的p1在E 和 NE间 那么该点的灰度值是由这两个分量构成。
p2同理在W 和 SW间。
如果中心点的灰度值小于p1 p2两个点的灰度,就将这点至为0
代码:
bool nonmax_suppress(double theta, Mat &g_mat, Point anchor, double *p1_v, double *p2_v)
{
//计算8邻域灰度
uchar N = g_mat.at(Point(anchor.x,anchor.y + 1));
uchar S = g_mat.at(Point(anchor.x,anchor.y - 1));
uchar W = g_mat.at(Point(anchor.x - 1,anchor.y));
uchar E = g_mat.at(Point(anchor.x + 1,anchor.y));
uchar NE = g_mat.at(Point(anchor.x + 1,anchor.y + 1));
uchar NW = g_mat.at(Point(anchor.x - 1,anchor.y + 1));
uchar SW = g_mat.at(Point(anchor.x - 1,anchor.y - 1));
uchar SE = g_mat.at(Point(anchor.x + 1,anchor.y - 1));
uchar M = g_mat.at(Point(anchor));
double angle = theta * 360 / (2 * CV_PI);//计算角度
//判定角度范围 计算 p1,p2插值
if(angle > 0 && angle < 45)
{
*p1_v = (1- tan(theta)) * E + tan(theta) * NE;
*p2_v = (1- tan(theta)) * W + tan(theta) * SW;
}
else if(angle >= 41 && angle < 90)
{
*p1_v = (1- tan(theta)) * NE + tan(theta) * N;
*p2_v = (1- tan(theta)) * SW + tan(theta) * S;
}
else if(angle >= 90 && angle < 135)
{
*p1_v = (1- tan(theta)) * N + tan(theta) * NW;
*p2_v = (1- tan(theta)) * S + tan(theta) * SE;
}
else
{
*p1_v = (1- tan(theta)) * NW + tan(theta) * W;
*p2_v = (1- tan(theta)) * SE + tan(theta) * E;
}
if(M < *p1_v || M < *p2_v) //非最大抑制
{
return false;
}
else
return true;
} (8)滞后双阈值化:
采用两个阈值
根据边缘响应灰度图。大于高阈值为强边缘,小于低阈值不是边缘。介于中间是弱边缘。
那么问题来了,弱边缘到底是边缘,还是由于噪点导致的梯度突变。
判定依据有多种。有的人是判定弱边缘点的8邻域中是否存在强边缘,如果有则将弱边缘设置成强的。没有就认为是假边缘。
另一种方案是用搜索算法,通过强边缘点,搜索8领域是否存在弱边缘,如果有,以弱边缘点为中心继续搜索,直到搜索不到弱边缘截止。
代码如下:
int bfs(Mat &mag, Mat &dst, int i, int j, int low)
{
int flag = 0;
if(dst.at(j, i) == 0)//没有搜索过
{
dst.at(j, i) = 255;//设置为255代表搜索过
for(int n = -1; n <= 1; n++)
{
for(int m = -1; m <= 1; m++)
{
if(m == 0 && n == 0) continue;
//如果点在图像内,并且高于低阈值
if(range(mag, i+n, j+m) && mag.at(j+m, i+n) >= low)
if(bfs(mag, dst, i+n, j+m, low))//迭代搜索直到搜索不到高于低阈值的点。
{
flag = 1;
break;
}
}
if(flag)
break;
}
return 1;
}
return 0;
} bool range(Mat &im, int x, int y)//判定点是否存在于图像内
{
if(x >= 0 && x < im.cols && y >= 0 && y < im.rows)
return true;
return false;
}综上所诉:
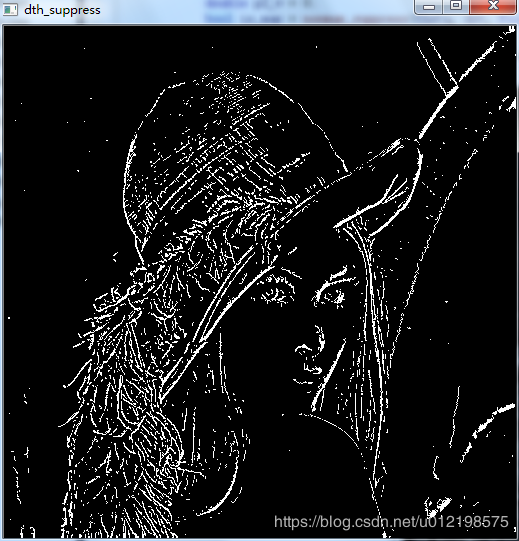
设置了高斯核大小为11,sigma设置为1.2。
得到处理后的图像:
大部分是显式出来了,不过还有一些细节问题,我就没去处理了。
当然步骤(1)~(6)并不是定死的,可以自己更替,也可以采用sobel算子,也可以用二阶。不过二阶会显示更多细节。
根据实际情况不同,采用的“准备”也可以不同。
快去实现自己的canny算法吧。