贪心算法1: 贪心的概念 最优装载问题
贪心算法的原理:
贪心算法总是做出当前最好的选择,也就是说,它期望通过局部最优选择从而得到全局最优的解决方案。
1. 没有后悔药,一旦做出选择,不可以后悔;
2. 有可能得到的不是最优解,而是最优解的近似解。
3. 选择什么样的贪心策略,直接决定算法的好坏。
贪心策略的基本思想
定义:贪心法是一种解决最优问题的策略。它是从问题的初始解出发,按照当前最佳的选择,把问题归纳为更小的相似的子问题,并使子问题最优,再由子问题来推导出全局最优解。
使用贪心方法需要注意局部最优与全局最优的关系,选择当前状态的局部最优并不一定能推导出问题的全局最优。
贪心算法求解的三个步骤:
a、确定贪心策略
b、根据贪心策略,一步一步得到局部最优解
c、将局部最优解合并起来就得到全局最优解
贪心策略的特点
1.贪心选择性质:所求问题的整体最优解可以通过一系列局部最优的选择来达到,这样的选择称为贪心选择。这些选择只依赖于以往所做过的选择,决不依赖于将来的选择。
2.最优子结构性质:当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
例题说明:
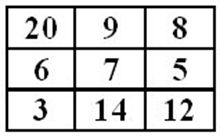
例题:有一个3*3的方格,每个格子有一个正整数,要求从每行格子中取一个数,使得取出来的3个数字之和最大(贪心)。
题目修改:规定从左下角出发,每次只能向上或向右移动一格,现在要求找出一条路径使得从左下角到达右上角所经过的格子中的数字之和最大,求最大值。
贪心方法:3→14→12→5→8=42(每次都找向上或者向右最大的一个)
最优解:3→6→20→9→8=46
局部最优无法带来全局最优,这就是不具备贪心选择性质。
什么样的问题能用贪心来求解:
利用贪心算法求解的问题往往具有两个重要的特性:贪心选择性质和最优子结构性质。
(1)贪心选择
所谓贪心选择性质是指原问题的整体最优解可以通过一系列局部最优的选择得到。
(2)最优子结构
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
动态规划的问题一般都不可以用贪心来解决。因为得到的不一定是全局最优解。
贪心策略与其他算法的区别:
1.贪心与递推:与递推不同的是,贪心法中推进的每一步不是依据某一固定的递推式,而是当前看似最佳的贪心决策,不断的将问题归纳为更加小的相似的子问题。
2.贪心与动态规划:与动态规划不同的是,贪心是鼠目寸光;动态规划是统揽全局。
贪心算法与其他算法的结合:竞赛的题目不仅仅直接地、单纯地考查贪心算法的应用,还经常综合在其他算法之中,比如在搜索算法中利用贪心计算一下最优值的上限和下限;又比如在动态规划算法中利用贪心得到状态的初始值等。
贪心的证明:
贪心策略能否适用,关键看在贪心的策略下,局部的最优解能否得到全局最优解。要看是否得到最优解,就要看贪心选择特征的证明了。常用的证明法有反证法和构造法。
1.反证法:顾名思义,对于当前的贪心策略,否定当前的选择,看看是否能得到最优解,如果不能得到,说明当前贪心策略是正确的;否则,当前策略不正确,不可用。
2.构造法:对于题目给出的问题,用贪心策略时,把问题构造成已知的算法或数据结构,以此证明贪心策略是正确的。
贪心的应用:
- 明显的贪心,一般此类应用问题本身就是贪心;
- 贪心数据结构,如:堆,胜者树;
- 可证明贪心策略的贪心,这是最常见的;
- 博弈、游戏策略,这些策略大多是贪心;
- 求较优解或多次逼近最优解;
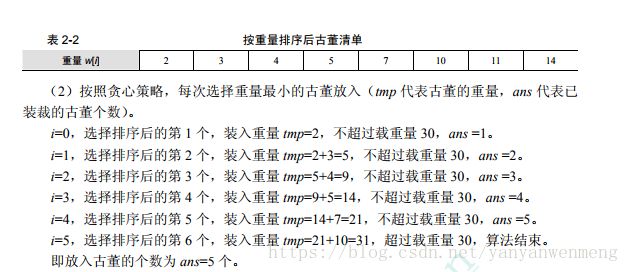
1. 最优装载问题
问题描述:某艘船的载重量为C,每件物品的重量为wi,要将尽量多的物品装入到船上。
分析:贪心策略:每次都选择最轻的,然后再从剩下的n-1件物品中选择最轻的。
算法策略:把n件物品 从小到大排序,然后根据贪心策略尽可能多的选出前i个物品,直到不能装为止。
#include
#include
#define MAXN 1000005
using namespace std;
int w[MAXN];//每件古董的重量
int main()
{
int c,n;//c:载重量,n古董数
int sum = 0;//装入古董的数量
int tmp = 0;//装入古董的重量
cin >> c >> n;
for(int i= 1; i <= n; ++i)
cin >> w[i];
sort(w+1,w+1+n);
for(int i = 1; i <= n; ++i)
{
tmp += w[i];//这个要在if外面
if(tmp <= c)
++sum;
else
break;
}
cout << sum << endl;
return 0;
}
代码优化:
#include
#include
#define MAXN 1000005
using namespace std;
int w[MAXN];//每件古董的重量
int main()
{
int c,n;//c:载重量,n古董数
int sum = n;//装入古董的数量
int tmp = 0;//装入古董的重量
cin >> c >> n;
for(int i= 1; i <= n; ++i)
cin >> w[i];
sort(w+1,w+1+n);
for(int i = 1; i <= n; ++i)
{
tmp += w[i];//这个要在if外面
if(tmp >= c)
{
if(tmp == c)//最后一个能装进去
sum = i;
else
sum = i-1;//最后一个不能装进去
break;
}
//其余的情况是tmp