内部排序（一）直接插入排序和二分插入排序

我们都知道，程序=数据结构+算法。数据结构和算法是密切相关的，因为不同的数据结构配合不同的算法，会有不同的效率。排序是最常见的算法之一，功能顾名思义是将一个数据对象（即数据元素的集合）重新排列成遵循某种规则的序列。例如在构建二叉搜索树的过程中也有排序的过（插入节点过程中左子树小于其父节点，右子树大于其父结点 ）程。排序是程序设计中的一种重要操作，因为对于无序的序列，进行查找操作时，我们只能用顺序查找的方法，这样平均查找长度为（n+1）/2，但是如果对有序的序列进行查找，我们可以用折半查找法，折半查找法的效率较高，平均查找长度为（（n+1）/n）*log（2n+1）-1（当n很大时，可以近似看作log（2n+1）-1），时间复杂度也是O（logN），所以说，排序是很重要的一种操作。

那么什么是内部排序？内部排序指的是，待排序列能够一次全部导入到内存空间里，也就是说有足够大的内存可以一次存放所有的待排序列，然后排序的过程是可以在内存中一次完成的。

排序算法中有一个常用的概念是“稳定性”，排序算法的稳定性指的是，对于任意的两个或以上相等的数据，如果排序前后它们的相对位置不发生改变，那么我们就说这个排序算法是稳定的。假设我们要对一个学生信息数据库表做排序，表中有两个学生的名字一样都是A，我们把它编号A1和A2，如果排序前A1排在A2前面，排序后A1仍然排在A2的前面，那么就说这个排序算法是稳定的，否则说是不稳定的。

下面几篇日志中我都会分享对一些排序算法的理解和实现的代码。

首先来看插入排序法。直接插入排序的思路是这样的：把待排序列分成两部分，前半部分是已经排好的序列，后半部分是待排列序列。假设序列里有N个元素，一开始第一个元素当作已排好序列，然后从序列第二个元素开始，每次从后面部分待排序列中拿出一个元素例如Tmp，与前面的已排好序列元素从后往前作比较，按照关系依次将元素往后挪，直到找到正确的位置了，就把Tmp插入进去。这样经过N-1次插入后，就能完成排序。我们直接来看个例子：

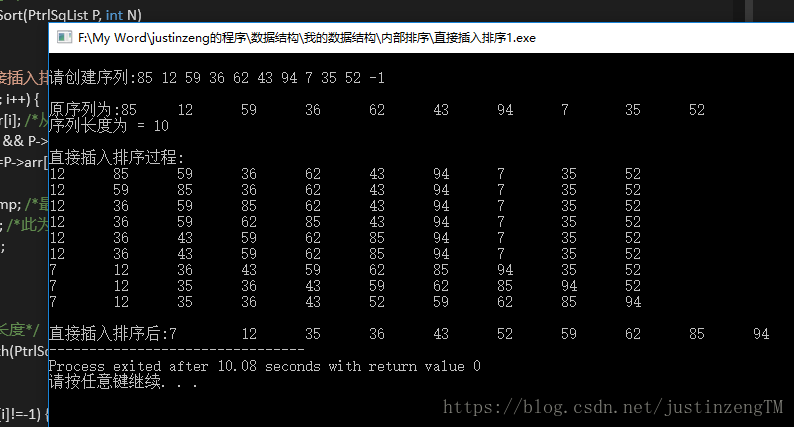
假设我们要对序列{85，12，59，36，62，43，94，7，35，52}从小到大升序排序（数组默认第一个元素下标为1）。按照前面的思路，首先把序列第一个元素85看作是已排好序列，第二个开始的元素都是待排序列。

1、首先从第二个元素开始，从待排序列中拿出一个元素，即把12赋给一个变量Tmp，然后Tmp与前面的已排好序列元素从后往前做比较，发现12比85小，那么85就往后挪一位到序列中的第二位。前面没元素了，所以12就插进去了第一个位置。序列变为：

{12，85，59，36，62，43，94，7，35，52}

2、然后继续把第三个元素59拿出来给Tmp，59和前面的已排好序列从后往前比较，发现59比85小，就把85往后挪一位到了第三个位置，59继续和前一位12比较。发现59比12大，那么就直接插入到第二位。序列变为：

{12，59，85，36，62，43，94，7，35，52}

3、继续往后到36拿出来，36比85小，85往后挪一位，继续36比59小，59往后挪，36大于12，那么就插入在第二位。序列为：

{12，36，59，85，62，43，94，7，35，52}。

就这样一直执行N-1步后，整个序列就排好了。那么代码要怎么写？

第72行开始，for循环从第二个元素开始拿出来给一个临时变量Tmp保存，然后嵌套一个for循环，因为是与待排序列从后往前比较，所以j从i开始，j>0 && P->arr[ j-1 ]>Tmp（也就是已排好序列中有元素比Tmp大），就把这个较大的元素往后挪一位，直到嵌套的for循环做完后，找到正确的插入位置j了，第77行就把Tmp插入进去。

 

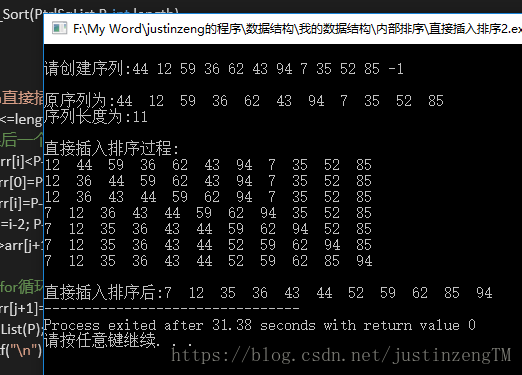
如果我们的序列是用一个数组来存储的，我们还可以利用数组的哨兵来暂时存放这个待排值，同样按照上面的思路可以写出一样方法的直接插入排序代码：

等于是哨兵P->arr[ 0 ]代替了Tmp值。

可是对于直接插入排序法来说，上述两种代码都用到了两个嵌套for循环，时间复杂度为O（N²），对于序列元素少的排序，这种方法简单易懂，但是当元素很多时，时间复杂度为O（N²）的排序法显然是不合适的。因此我们要么采用其他排序方法，要么可以尝试改进下直接插入排序法。

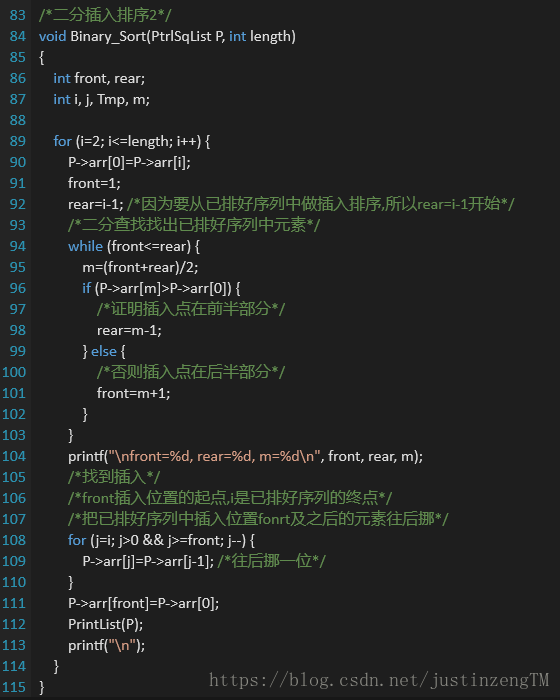
改进直接插入排序法，我们可以想想，从待排序列中拿出一个元素与已排好序列每一个元素作比较，找出合适的位置做插入，是一个“查找过程”，而已排好序列中的元素又是有序的，因此我们可以用二分查找的方法做插入排序，这样就可以减少元素之间比较的次数了。代码如下：

把上面第一种方法改一下，就是通过二分查找找出已排好序列中插入的位置，然后第107行，从插入位置front为起点，已排好序列终点i为终点，把插入位置即后面的元素都往后挪一位，腾出插入位置front来，最后把Tmp插入即可。

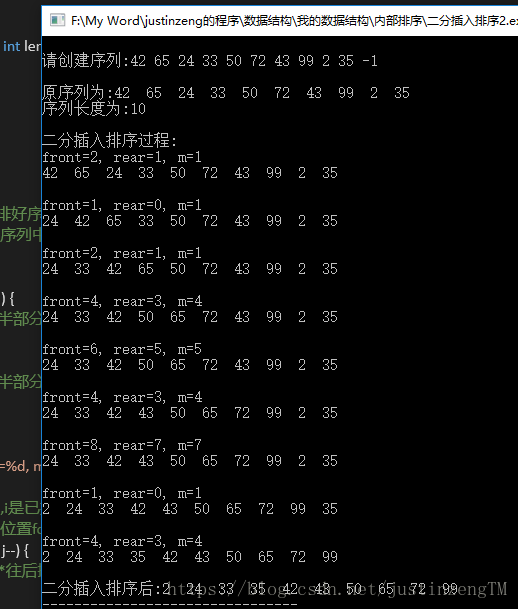
      同样的方法我们可以对上面的方法二设置哨兵的方法也改一下：

折半插入排序的空间复杂度和直接插入排序一样，折半插入排序减少了元素之间的比较次数，但是元素的移动次数不变，所以时间复杂度仍为O（n²）。

上述四种方法完整代码在个人代码云：

https://gitee.com/justinzeng/codes/e1z4qor752bldtjkcfp6n92

https://gitee.com/justinzeng/codes/9fql2gtorkwd71jbc3nyv44

https://gitee.com/justinzeng/codes/0ifwzn6am39t85h7lq1ek79

https://gitee.com/justinzeng/codes/1xc8f2pa9u7vkbedqsti061