归并排序(非递归实现)

我们知道，递归实现的缺点就是会一直调用栈，而栈内存往往是很小的。所以，我们尝试着用循环的办法去实现归并排序。

之气提到过，归并排序的基本思路是将待排序序列R[0…n-1]看成是n个长度为1的有序序列，将相邻的有序表成对归并，得到n/2个长度为2的有序表；将这些有序序列再次归并，得到n/4个长度为4的有序序列；如此反复进行下去，最后得到一个长度为n的有序序列。

综上可知：

归并排序其实要做两件事：

（1）“分解”——将序列每次折半划分。

（2）“合并”——将划分后的序列段两两合并后排序。

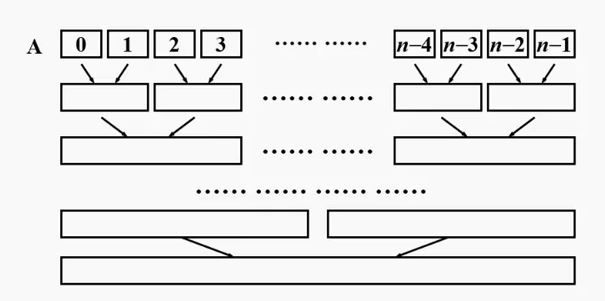
具体过程如下图所示：

1.待排序序列R[0…n-1] 一共有n个有序的子序列，每个子序列里都只含有一个元素。
2. 某趟归并中，设各子表的长度为length，则归并前R[0…n-1]中共有n/length个有序的子表：R[0…length-1], R[gap…2*length-1], … , R[(n/length)*length … n-1]。
3. 在上面归并的时候，我们遇到的length（1，2，4，8…)很可能不会在最终结果等于n。比如：n=7。这时候，我们采取的一种办法是只归并前面最接近n的那个位置（i+2*length<=n，即i<=n-2*length，处理到倒数第二对)。剩下的就通过下面代码来实现：

if ( i+length < N ) /*说明i+一个子序列的长度*/
         Merge( A, TmpA, i, i+length, N-1);/* 归并最后2个子列*/
     else /* 最后只剩1个子列*/
         for ( j = i; j < N; j++ ) TmpA[j] = A[j];

n=7的示意图：

。

完整代码：

#include "stdio.h"
#include "stdlib.h"

void Merge( int A[], int TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
     int LeftEnd, NumElements, Tmp;
     int i;

     LeftEnd = R - 1; /* 左边终点位置 */
     Tmp = L;         /* 有序序列的起始位置 */
     NumElements = RightEnd - L + 1;

     while( L <= LeftEnd && R <= RightEnd ) {
         if ( A[L] <= A[R] )
             TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
         else
             TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
     }

     while( L <= LeftEnd )
         TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
     while( R <= RightEnd )
         TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
    /*for( i = 0; i < NumElements; i++, RightEnd -- )
         A[RightEnd] = TmpA[RightEnd];  将有序的TmpA[]复制回A[] */
}

/* length = 当前有序子列的长度*/
void Merge_pass( int A[], int TmpA[], int N, int length )
{ /* 两两归并相邻有序子列 */
     int i, j;

     for ( i=0; i <= N-2*length; i += 2*length )
         Merge( A, TmpA, i, i+length, i+2*length-1 );
     if ( i+length < N )  
     /*  i+一个序列还是小于n,意味着有两个长度不等的子序列，其中一个为length，后一个小于length */
         Merge( A, TmpA, i, i+length, N-1);  /* 归并最后2个子列*/
     else /* 最后只剩1个子列*/
         for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}

void Merge_Sort( int A[], int N )
{
     int length;
     int *TmpA;

     length = 1; /* 初始化子序列长度*/
     TmpA = (int*)malloc( N * sizeof( int ) );
     if ( TmpA != NULL ) {
          while( length < N ) {
              Merge_pass( A, TmpA, N, length );
              length *= 2;
              Merge_pass( TmpA, A, N, length );
              length *= 2;
          }
          free( TmpA );
     }
     else printf( "空间不足" );
}

int main()
{
    int a[10]={3,1,7,10,9,2,5,4,6,8};
    //int a[10]= {13,53,0,21,89,76,91,23,44,32};
    Merge_Sort(a,10);
    for(int i = 0;i<10;i++)
        printf("%d ",a[i]);
    return 0;
}

当然，我们在上面代码的第24行中，将原先递归实现时每次归并后保存在TempA[]数组的值传回给A[] 的步骤注释了，同时在 Merge_Sort( int A[], int N ) 函数中，我们每次循环都 Merge_pass 两次：

while( length < N ) {
      Merge_pass( A, TmpA, N, length );
      length *= 2;
      Merge_pass( TmpA, A, N, length );
      length *= 2;
 }

这样可以确保我们将序列归并排序后的数据一定是保存在数组A[]中。
如果每次都在每次归并的时候，加上那句for语句，那么也就是每次都将排序结果传回给数组A[]，也能确保排序后的值在数组A[]中。但是这样处理的过程和原先的过程是有却别的，现在的过程是：

1. 归并
2. 调用Merge将相邻的子表归并时，必须对表的特殊情况进行特殊处理：
   若子表个数为奇数，则最后一个子表无须和其他子表归并（即本趟处理轮空）：若子表个数为偶数，则要注意到最后一对子表中后一个子表区间的上限为n-1。
   示意图如下：
   

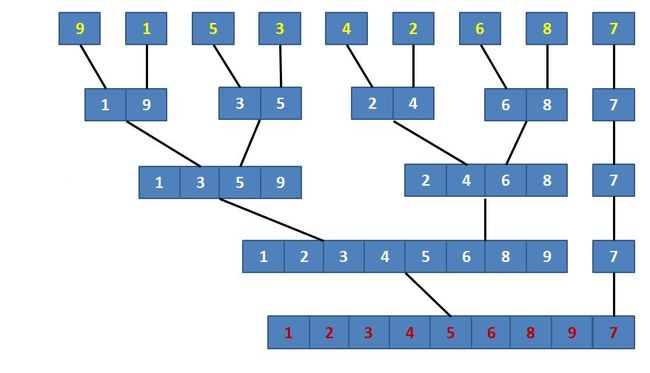
从n=7和n=9的两幅图就可以看出，一个是每次所有元素都进行归并了，一个是将残留项（最后一项的长度小于length）保留，直到最后再归并。

所以也可以将代码改写如下：

#include "stdio.h"
#include "stdlib.h"

void Merge( int A[], int TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
     int LeftEnd, NumElements, Tmp;
     int i;

     LeftEnd = R - 1; /* 左边终点位置 */
     Tmp = L;         /* 有序序列的起始位置 */
     NumElements = RightEnd - L + 1;

     while( L <= LeftEnd && R <= RightEnd ) {
         if ( A[L] <= A[R] )
             TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
         else
             TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
     }

     while( L <= LeftEnd )
         TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
     while( R <= RightEnd )
         TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
   for( i = 0; i < NumElements; i++, RightEnd -- )
         A[RightEnd] = TmpA[RightEnd];   /*将有序的TmpA[]复制回A[] */
}

/* length = 当前有序子列的长度*/
void Merge_pass( int A[], int TmpA[], int N, int length )
{ /* 两两归并相邻有序子列 */
     int i, j;

     for ( i=0; i <= N-2*length; i += 2*length )
         Merge( A, TmpA, i, i+length, i+2*length-1 );
     if ( i+length < N ) /* 归并最后2个子列*/
         Merge( A, TmpA, i, i+length, N-1);
     //else /* 最后只剩1个子列*/
       //  for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}

void Merge_Sort( int A[], int N )
{
     int length;
     int *TmpA;

     length = 1; /* 初始化子序列长度*/
     TmpA = (int*)malloc( N * sizeof( int ) );
     if ( TmpA != NULL ) {
          while( length < N ) {
              Merge_pass( A, TmpA, N, length );
              length *= 2;
              //Merge_pass( TmpA, A, N, length );
              //length *= 2;
          }
          free( TmpA );
     }
     else printf( "空间不足" );
}

int main()
{
    int a[10]={3,1,7,10,9,2,5,4,6,8};
    //int a[10]= {13,53,0,21,89,76,91,23,44,32};
    Merge_Sort(a,10);
    for(int i = 0;i<10;i++)
        printf("%d ",a[i]);
    return 0;
}