论文笔记: Monocular Object Orientation Estimation using Riemannian Regression and Classification Network
这篇文章做的是从单目图像中使用CNN预测刚体目标的朝向。所谓朝向其实就是相机位姿中旋转部分,即目标在相机坐标系中旋转。
之前也有过这种想法,将目标的检测中的anchor机制引入到旋转量的估计中。将2D旋转空间分为若干个关键位置,给定一张输入图片先预测最近的关键位置,再预测一个在该关键位置上的偏移量,得到最终的旋转量的估计。这样做的方法既可以避免了建立离散图像检索库造成的离散问题,也可以一定程度上解决直接回归旋转量的不稳定性问题。
这篇文章程度上实现了这种想法,并对这种方法的各种变种进行了实验和分析,很有借鉴意义。
文章题目中的黎曼其实只是旋转量的一种度量方式,也就是常用的李群表示的旋转量,李代数表示旋转增量,李代数到李群的指数映射,有一些摄影测量基础和机器人学基础不难理解这一点,其实并不是很高大上。
Introduction
现有工作
基于CNNs的单目目标位姿估计大体上可以分为以下几类:
- 间接法:先在图像检测得到目标上已知三维坐标的关键点,先建立2D-3D对应关系,然后使用PnP方法求解位姿
- 直接法:又可以分为回归与分类。分类法中将朝向空间离散化,打上标签,预测每个输出图像的标签;回归法中每个训练样本都对应一个旋转量的表示,例如四元数、欧拉角等,以此训练CNN。
这篇文章关注的重点是直接法。现有工作的缺点是使用的旋转量的表示方法以及损失函数没有考虑到旋转空间的几何特性。 基于分类的方法需要将旋转空间离散化,导致误差不可能为0。其次当bins比较粗糙时,误差会更大。基于回归方法的问题是旋转量的欧拉角表示方法忽略了旋转空间中测地距离(geodesic distance),另一个问题是对预测的旋转量缺少一个置信度评价。
现有方法的另外一个问题是网络的结构与训练方法并不是为旋转量估计设计的,例如数据增强方法等。
文章贡献
- 使用旋转向量和四元数作为网络是输出,使用测地线距离设计损失函数;
- 设计了一种旋转量分类和回归框架,称为 B i n & D e l t a Bin\: \&\: Delta Bin&Delta模型,其中 B i n Bin Bin解决旋转量分为问题, D e l t a Delta Delta解决旋转量到分类中离散点的回归问题;
- 设计了一种3D数据增强方式,3D pose jittering;
- 在Pascal3D+上的实验得到了state-of-the-art的表现。
3D旋转
表示形式
欧拉角、旋转角、四元数
3D旋转空间中的损失函数
测地线距离:
d ( R 1 , R 2 ) = ∥ l o g m ( R 1 R 2 T ) ∥ F 2 d(R_1,R_2) = \frac{\|\mathrm{logm}(R_1R_2^T) \|_F}{\sqrt 2} d(R1,R2)=2∥logm(R1R2T)∥F
该距离实际上旋转向量的夹角,另外一种计算方式为:
d ( R 1 , R 2 ) = ∣ cos − 1 [ t r ( R 1 T R 2 ) − 1 2 ] ∣ d(R_1,R_2) =| \cos^{-1}\left[\frac{tr(R_1^TR_2) - 1}{2}\right]| d(R1,R2)=∣cos−1[2tr(R1TR2)−1]∣
用于旋转估计的测地回归
网络结构
网络分为特征提取和朝向估计两部分, f = Φ F ( x ; W F ) f=\Phi_F(x;W_F) f=ΦF(x;WF)和 y = Φ P ( f ; W P ) y=\Phi_P(f;W_P) y=ΦP(f;WP)。使用旋转角 y ∈ R 3 y\in\mathbb{R}^3 y∈R3表示旋转量,对于四元数,需要添加一个单位化约束。
损失函数
-
旋转角表示:
L R ( y 1 , y 2 ) = d ( R 1 , R 2 ) \mathcal{L}_R(y_1, y_2) = d(R_1, R_2) LR(y1,y2)=d(R1,R2)
其中 R i = exp ( y i ) R_i=\exp(y_i) Ri=exp(yi),值得注意的是测地距离 L R ( y 1 , y 2 ) \mathcal{L}_R(y_1, y_2) LR(y1,y2)并不等于 L E ( y 1 , y 2 ) = ∥ y 1 − y 2 ∥ 2 2 \mathcal{L}_E(y_1, y_2)=\|y_1-y_2\|_2^2 LE(y1,y2)=∥y1−y2∥22 -
四元数表示:
d ( q 1 , q 2 ) = 2 cos − 1 ( ∣ c ∣ ) , w h e r e ( c , s ) = q 1 − 1 ⋅ q 2 d(q_1, q_2) = 2\cos^{-1}(|c|), \mathrm{where}\quad (c, s) = q_1^{-1}\cdot q_2 d(q1,q2)=2cos−1(∣c∣),where(c,s)=q1−1⋅q2
也可以表示成:
m a t h c a l L R ( q 1 , q 2 ) = 2 cos − 1 ( ∣ ⟨ q 1 , q 2 ⟩ ∣ ) \\mathcal{L}_R(q_1, q_2)=2\cos^{-1}(|\langle q_1, q_2\rangle|) mathcalLR(q1,q2)=2cos−1(∣⟨q1,q2⟩∣)
测地线回归模型:
R G : min W 1 N ∑ L R ( y n ∗ , y n ) \mathcal{R}_G: \min_W\frac{1}{N}\sum\mathcal{L}_R(y_n^*, y_n) RG:WminN1∑LR(yn∗,yn)
BaseLines
选择了两种常见的网络作为baseline。
- 欧式回归模型
E G : min W 1 N ∑ ∥ R ( y n ∗ , y n ) ∥ 2 2 \mathcal{E}_G: \min_W\frac{1}{N}\sum\|R(y_n^*, y_n)\|_2^2 EG:WminN1∑∥R(yn∗,yn)∥22 - 分类模型
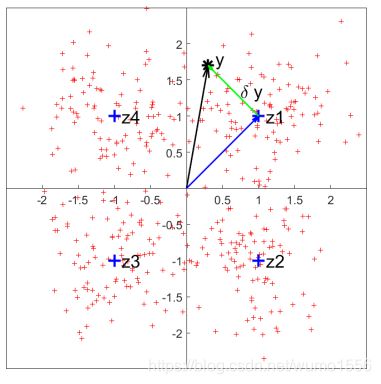
从位姿空间中选择 K K K个关键位姿 { z k ∈ R 3 } k = 1 K \{z_k\in \mathbb{R}^3\}_{k=1}^K {zk∈R3}k=1K,应的label为 l ∈ { 1 , … , K } l\in \{1, \dots, K\} l∈{1,…,K}。
训练时,采用欧式距离度量,对每个样本 y n ∗ y^*_n yn∗,训练时标签真值为:
l n ∗ = a r g m i n k ∥ y n ∗ − z k ∥ 2 l^*_n= \mathrm{argmin}_k\|y^*_n-z_k\|_2 ln∗=argmink∥yn∗−zk∥2
测试时,对网络输出的标签 l n l_n ln,其旋转量为 y n = z l n y_n=z_{l_n} yn=zln
用于旋转估计的混合分类-回归网络
文章指出了纯回归方法难以对具有对称性质的目标类别的多模态姿态分布进行建模,一个解决思路是:
- 先预测一个相对于若干关键位姿的离散位姿标签概率分布;
- 再预测一个相对于若干关键位姿的连续位姿偏移回归值;
- 最后使用结合函数将离散位姿预测值和连续位姿回归值结合起来。
模型结构
模型可以分为三个部分,特征提取网络、用于分类的 B i n Bin Bin和用于回归的 D e l t a Delta Delta。 W = [ W F , W B c , W D c ] W=[W_F, {W_B^c}, {W_D^c}] W=[WF,WBc,WDc]。
标签值 l = Φ B ( f ; W B c ) l=\Phi_B(f;W_B^c) l=ΦB(f;WBc),其中 Φ B \Phi_B ΦB是有参数 W B c W_B^c WBc定义的 B i n Bin Bin网络, W B c W_B^c WBc为目标的类别, l l l是关键位姿 z l z_l zl的标签。 D e l t a Delta Delta网络预测一个位姿残差 δ y = Φ D ( f ; W D c ) \delta_y=\Phi_D(f;W_D^c) δy=ΦD(f;WDc)。给定一个分类的输出,即类别 l l l和位姿残差 δ y \delta_y δy,结合方法为:
y = g ( z l , δ y ) y=g(z_l, \delta y) y=g(zl,δy)
其中, g ( ⋅ , ⋅ ) g(\cdot,\cdot) g(⋅,⋅)为某种结合函数。
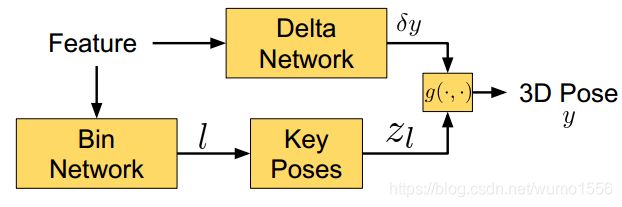
可以选择是否为分类网络中的每个关键位姿分配一个 D e l t a Delta Delta网络,还是所有关键位姿使用一个共同的关键位姿。若是每个位姿分配一个 D e l t a Delta Delta网络,位姿残差输出也是标签的函数, δ y → δ y l \delta y\rightarrow \delta y^l δy→δyl。
损失函数
损失函数由 B i n Bin Bin和 D e l t a Delta Delta的输出构成:
L ( y 1 , y 2 ) = α L R ( g ( z l 1 , δ y 1 ) , g ( z l 2 , δ y 2 ) ) + L C ( l 1 , l 2 ) \mathcal{L}(y_1, y_2) = \alpha \mathcal{L}_{R}(g(z_{l{_1}}, \delta{y_1}), g(z_{l{_2}}, \delta{y_2})) + \mathcal{L}_C(l_1, l_2) L(y1,y2)=αLR(g(zl1,δy1),g(zl2,δy2))+LC(l1,l2)
旋转变量 y 1 = g ( z l 1 , δ y 1 ) y_1=g(z_{l_1}, \delta y_1) y1=g(zl1,δy1)和 y 2 = g ( z l 2 , δ y 2 ) y_2=g(z_{l_2}, \delta y_2) y2=g(zl2,δy2)可以采用四元数和旋转向量表示。
模型
通过结合不同的模型结构、损失函数以及旋转变量的表示形式,可以得到多种模型:
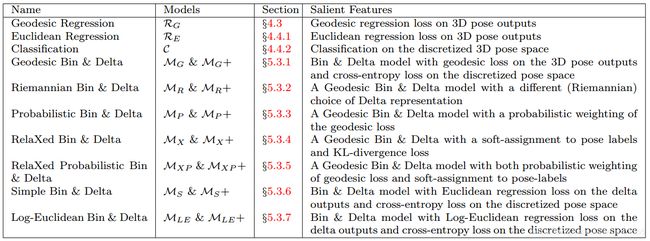
其中 + + +号表示采用One- D e l t a Delta Delta-Per- B i n Bin Bin结构。
Geodesic Bin & Delta Model
采用欧式距离建立结合函数:
g ( z l , δ y ) = z l + δ y g(z_l, \delta_y)=z_l+\delta_y g(zl,δy)=zl+δy
对于四元数表示的旋转量,需要添加 L 2 L_2 L2正则化:
g ( z l , δ y ) = z l + δ y ∥ z l + δ y ∥ 2 g(z_l, \delta_y)=\frac{z_l+\delta_y}{\|z_l+\delta_y\|_2} g(zl,δy)=∥zl+δy∥2zl+δy
两种模型为:
M G : min W 1 N ∑ n [ α L R ( y n ∗ , z l n + δ y n ) + L C ( l n ∗ , l n ) ] \mathcal{M}_G: \min_W\frac{1}{N}\sum_n\left[\alpha\mathcal{L}_R(y_n^*, z_{l_n}+\delta y_n)+\mathcal{L}_C(l_n^*,l_n)\right] MG:WminN1n∑[αLR(yn∗,zln+δyn)+LC(ln∗,ln)]
M G + : min W 1 N ∑ n [ α L R ( y n ∗ , z l n + δ y n l n ) + L C ( l n ∗ , l n ) ] \mathcal{M}_G+: \min_W\frac{1}{N}\sum_n\left[\alpha\mathcal{L}_R(y_n^*, z_{l_n}+\delta y^{l_n}_n)+\mathcal{L}_C(l_n^*,l_n)\right] MG+:WminN1n∑[αLR(yn∗,zln+δynln)+LC(ln∗,ln)]
一种简单的模型,采用四个关键位姿的Geodesic Bin & Delta Model为:
Riemannian Bin & Delta Model
采用指数映射建立结合函数:
g ( z l , δ y ) = log ( exp ( z l ) exp ( δ y ) ) g(z_l, \delta_y)=\log(\exp(z_l)\exp(\delta y)) g(zl,δy)=log(exp(zl)exp(δy))
旋转量的输出为: R = R ~ exp ( δ y ) R = \tilde{R}\exp(\delta y) R=R~exp(δy)
模型为:
M G : min W 1 N ∑ n [ α L R ( R n ∗ , z l n + R ~ l n exp ( δ y n ) ) + L C ( l n ∗ , l n ) ] \mathcal{M}_G: \min_W\frac{1}{N}\sum_n\left[\alpha\mathcal{L}_R(R_n^*, z_{l_n}+\tilde{R}_{l_n}\exp(\delta y_n))+\mathcal{L}_C(l_n^*,l_n)\right] MG:WminN1n∑[αLR(Rn∗,zln+R~lnexp(δyn))+LC(ln∗,ln)]
M G + : min W 1 N ∑ n [ α L R ( R n ∗ , z l n + R ~ l n exp ( δ y n l n ) ) + L C ( l n ∗ , l n ) ] \mathcal{M}_G+: \min_W\frac{1}{N}\sum_n\left[\alpha\mathcal{L}_R(R_n^*, z_{l_n}+\tilde{R}_{l_n}\exp(\delta y^{l_n}_n))+\mathcal{L}_C(l_n^*,l_n)\right] MG+:WminN1n∑[αLR(Rn∗,zln+R~lnexp(δynln))+LC(ln∗,ln)]
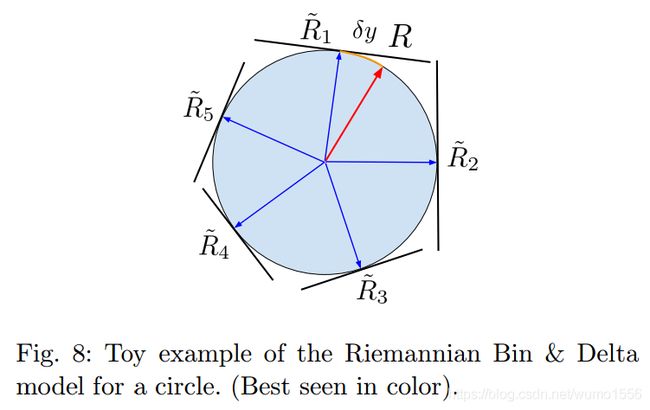
由于指数映射只能在旋转角的表示下使用,因此这种模型不能使用四元数。
Probabilistic Bin & Delta Model
该模型是Geodesic Bin & Delta model的变种,使用 B i n Bin Bin网络输出的标签得分对 D e l t a Delta Delta网络进行加权。对第n张输出图像,第k个bin的得分为 p n k p_{nk} pnk,其中 k = 1 , 2 , … , K k=1, 2, \dots, K k=1,2,…,K。以 B i n Bin Bin网络对最终输出的位姿进行加权,得到的模型为:
M G : min W 1 N ∑ n [ α ∑ k p n k L R ( y n ∗ , z k + δ y n ) + L C ( l n ∗ , l n ) ] \mathcal{M}_G: \min_W\frac{1}{N}\sum_n\left[\alpha\sum_kp_{nk}\mathcal{L}_R(y_n^*, z_k+\delta y_n)+\mathcal{L}_C(l_n^*,l_n)\right] MG:WminN1n∑[αk∑pnkLR(yn∗,zk+δyn)+LC(ln∗,ln)]
M G + : min W 1 N ∑ n [ α ∑ k p n k L R ( y n ∗ , z k + δ y n k ) + L C ( l n ∗ , l n ) ] \mathcal{M}_G+: \min_W\frac{1}{N}\sum_n\left[\alpha\sum_kp_{nk}\mathcal{L}_R(y_n^*, z_k+\delta y^k_n)+\mathcal{L}_C(l_n^*,l_n)\right] MG+:WminN1n∑[αk∑pnkLR(yn∗,zk+δynk)+LC(ln∗,ln)]
RelaXed Bin & Delta
前几种模型都是采用了对每张图片分配了关键位姿,一种更加灵活的模型采用柔性的分配方法,为每幅图像分配一个概率图,方法为:
p n k ∗ = exp ( − γ ∥ y n ∗ − z k ∥ 2 2 ) ∑ k exp ( − γ ∥ y n ∗ − z k ∥ 2 2 ) p^*_{nk}=\frac{\exp{(-\gamma\|y_n^*-z_k\|_2^2)}}{\sum_k\exp{(-\gamma\|y_n^*-z_k\|_2^2)}} pnk∗=∑kexp(−γ∥yn∗−zk∥22)exp(−γ∥yn∗−zk∥22)
两种模型为:
M X : min W 1 N ∑ n [ α L R ( R n ∗ , z l n + δ y n ) + L K D ( p n ∗ , p n ) ] \mathcal{M}_X: \min_W\frac{1}{N}\sum_n\left[\alpha\mathcal{L}_R(R_n^*, z_{l_n}+\delta y_n)+\mathcal{L}_{KD}(p_n^*,p_n)\right] MX:WminN1n∑[αLR(Rn∗,zln+δyn)+LKD(pn∗,pn)]
M X + : min W 1 N ∑ n [ α L R ( R n ∗ , z l n + δ y n l n ) + L K D ( p n ∗ , p n ) ] \mathcal{M}_X+: \min_W\frac{1}{N}\sum_n\left[\alpha\mathcal{L}_R(R_n^*, z_{l_n}+\delta y^{l_n}_n)+\mathcal{L}_{KD}(p_n^*,p_n)\right] MX+:WminN1n∑[αLR(Rn∗,zln+δynln)+LKD(pn∗,pn)]
其中, L K D ( ⋅ , ⋅ ) \mathcal{L}_{KD}(\cdot, \cdot) LKD(⋅,⋅)为真值与预测值Kullback-Leibler divergence; p n ∗ = [ p n k ∗ ] k = 1 K p_n^*=[p^*_{nk}]^K_{k=1} pn∗=[pnk∗]k=1K, p n = [ p n k ] k = 1 K p_n=[p_{nk}]^K_{k=1} pn=[pnk]k=1K。
RelaXed Probabilistic Bin & Delta Model
对于RelaXed Bin & Delta Model也可以采用 B i n Bin Bin网络输出的概率分布对 D e l t a Delta Delta网络进行加权:
M X : min W 1 N ∑ n [ α ∑ k p n k L R ( R n ∗ , z l n + δ y n ) + L K D ( p n ∗ , p n ) ] \mathcal{M}_X: \min_W\frac{1}{N}\sum_n\left[\alpha\sum_kp_{nk}\mathcal{L}_R(R_n^*, z_{l_n}+\delta y_n)+\mathcal{L}_{KD}(p_n^*,p_n)\right] MX:WminN1n∑[αk∑pnkLR(Rn∗,zln+δyn)+LKD(pn∗,pn)]
M X + : min W 1 N ∑ n [ α ∑ k p n k L R ( R n ∗ , z l n + δ y n l n ) + L K D ( p n ∗ , p n ) ] \mathcal{M}_X+: \min_W\frac{1}{N}\sum_n\left[\alpha\sum_kp_{nk}\mathcal{L}_R(R_n^*, z_{l_n}+\delta y^{l_n}_n)+\mathcal{L}_{KD}(p_n^*,p_n)\right] MX+:WminN1n∑[αk∑pnkLR(Rn∗,zln+δynln)+LKD(pn∗,pn)]
Simple Bin & Delta Model
前面几种模型的 Δ \Delta Δ网络损失是定义在结合函数之后,即损失是针对整体网络输出而言。另外一种的建立 D e l t a Delta Delta网络的损失:
M X : min W 1 N ∑ n [ α ∥ δ y n ∗ − δ y n ∥ 2 2 + L C ( l n ∗ , l n ) ] \mathcal{M}_X: \min_W\frac{1}{N}\sum_n\left[\alpha \|\delta y^*_n -\delta y_n\|_2^2+\mathcal{L}_{C}(l_n^*,l_n)\right] MX:WminN1n∑[α∥δyn∗−δyn∥22+LC(ln∗,ln)]
M X + : min W 1 N ∑ n [ α ∥ δ y n ∗ − δ y n l n ∥ 2 2 + L C ( l n ∗ , l n ) ] \mathcal{M}_X+: \min_W\frac{1}{N}\sum_n\left[\alpha\|\delta y^*_n -\delta y^{l_n}_n\|_2^2+\mathcal{L}_{C}(l_n^*,l_n)\right] MX+:WminN1n∑[α∥δyn∗−δynln∥22+LC(ln∗,ln)]
Log-Euclidean Bin & Delta Model
Riemannian Bin & Delta 模型中,旋转量真值与预测值间的测地距离可以由切空间在单位1上的欧式距离近似:
L ( R n ∗ , R ~ l n exp ( δ y n ) ) = L ( R ~ l n T R n ∗ , exp ( δ y n ) ) ≈ ∥ log ( R ~ l n T R n ∗ ) − log ( exp ( δ y n ) ) ∥ 2 \mathcal{L}(R^*_n, \tilde{R}_{l_n}\exp(\delta y_n))=\mathcal{L}(\tilde{R}_{l_n}^TR^*_n, \exp(\delta y_n))\approx \|\log(\tilde{R}_{l_n}^TR^*_n) - \log(\exp(\delta y_n))\|_2 L(Rn∗,R~lnexp(δyn))=L(R~lnTRn∗,exp(δyn))≈∥log(R~lnTRn∗)−log(exp(δyn))∥2
当 ( R ~ l n T R n ∗ ) (\tilde{R}_{l_n}^TR^*_n) (R~lnTRn∗)越接近与 I I I,近似程度越高,其实就是李群李代数里的一套。
M X : min W 1 N ∑ n [ α ∥ log ( R ~ l n T R n ∗ ) − δ y n ∥ 2 2 + L K D ( l n ∗ , l n ) ] \mathcal{M}_X: \min_W\frac{1}{N}\sum_n\left[\alpha \|\log(\tilde{R}_{l_n}^TR^*_n) -\delta y_n\|_2^2+\mathcal{L}_{KD}(l_n^*,l_n)\right] MX:WminN1n∑[α∥log(R~lnTRn∗)−δyn∥22+LKD(ln∗,ln)]
M X + : min W 1 N ∑ n [ α ∥ log ( R ~ l n T R n ∗ ) − δ y n l n ∥ 2 2 + L K D ( l n ∗ , l n ) ] \mathcal{M}_X+: \min_W\frac{1}{N}\sum_n\left[\alpha\|\log(\tilde{R}_{l_n}^TR^*_n) -\delta y^{l_n}_n\|_2^2+\mathcal{L}_{KD}(l_n^*,l_n)\right] MX+:WminN1n∑[α∥log(R~lnTRn∗)−δynln∥22+LKD(ln∗,ln)]
3D Pose Jittering 数据增强
三维的旋转为 R ( a z , e l , c t ) = R Z ( c t ) R X ( e l ) R Y ( a z ) R(az, el, ct) = R_Z(ct)R_X(el)R_Y(az) R(az,el,ct)=RZ(ct)RX(el)RY(az)。绕z轴的旋转会造成相平面内的旋转,而绕x、y轴的旋转会造成图像外的变化,即深度上的变化。作者在camera-tilt和azimuth上进行微小扰动,得到3D pose jittering。
实验
数据集:Pascal3D+
评价指标:
- M e d E r r = m e d i a n n = 1 N ∠ ( R n ∗ , R n ) = m e d i a n n = 1 N ∣ cos − 1 ( t r ( R n T R n ∗ ) − 1 2 ) ∣ MedErr=\mathrm{median}^N_{n=1}\angle(R^*_n, R_n)=\mathrm{median}^N_{n=1}\left|\cos^{-1}(\frac{tr(R_n^TR_n^*)-1}{2})\right| MedErr=mediann=1N∠(Rn∗,Rn)=mediann=1N∣∣∣cos−1(2tr(RnTRn∗)−1)∣∣∣
- A c c π 6 = 1 N ∑ n = 1 N 1 [ ∠ ( R n ∗ , R n ) ≤ 3 0 ∘ ] Acc_\frac{\pi}{6}=\frac{1}{N}\sum_{n=1}^N\mathbf{1}[\angle(R^*_n, R_n)\le30^\circ] Acc6π=N1∑n=1N1[∠(Rn∗,Rn)≤30∘]
- A R P θ ARP_\theta ARPθ: detected bbox I O U > 0.5 IOU > 0.5 IOU>0.5 and ∠ ( R n ∗ , R n ) ≤ θ \angle(R^*_n, R_n)\le \theta ∠(Rn∗,Rn)≤θ, θ = 3 0 ∘ \theta =30^\circ θ=30∘
- A V P K AVP_K AVPK: detected bbox I O U > 0.5 IOU > 0.5 IOU>0.5 and l ( a z ∗ ) = = l ( a z ) \mathcal{l}(az*) == \mathcal{l}(az) l(az∗)==l(az),即 a z az az的标签正确, K=4, 8, 16, 32
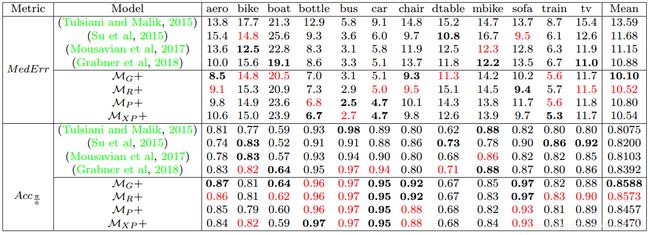
结合文章中的其他实验,表现比较好的模型是Riemannian Bin & Delta Model和Geodesic Bin & Delta Model。概率加权、松弛等对两种基础模型的效果并不好。