论文笔记:ROI-10D: Monocular Lifting of 2D Detection to 6D Pose and Metric Shape
1introduction
这篇cvpr2019文章提出了一种度量精确的单目3D目标检测端对端方法。(arxiv:1812.02781)
主要贡献有三点:
- 一种度量精确的单目3D目标检测端对端方法,包括一种可微分的2D ROI到3D ROI 提升映射,并提供了用于回归3D box 实例的所有组件;
- 一种用于在度量空间对其3D box的损失函数,直接优化其关于真值的误差;
- 扩展模型,将其用于预测度量纹理面片,保证了进一步的3D 推理,包括3D 一致性仿真数据增强。
称该模型为"ROI-10D",将2D ROI提升到3D ROI需要6自由度的位姿参数,3个自由度的空间体积,和一个形状自由度。
2 相关工作
3 用于位姿和形状估计的单目10D提升
分三个部分介绍了方法:
- 模型结构
- 用于3D的损失函数
- 学习得到的度量形状空间,以及如何使用估计的形状参数进行3D重建
3.1 端到端的单目结构
类似于Faster RCNN,首先检测2D区域的proposals,然后为每个proposal region执行分支预测。2D proposals使用了FPN-ResNet34,并使用了focal loss加权。对每个检测到的proposal region使用ROIAlign 提取用于预测分支的特征。
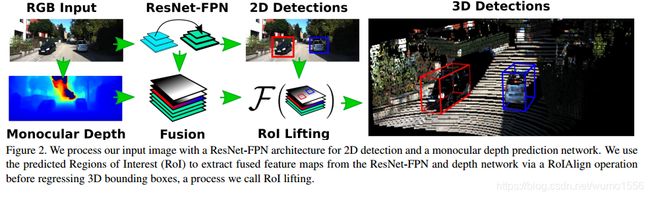
由于信息缺失和重投影模糊,从单目图像中直接回归3D信息是病态、不稳定的。该文献使用了state-of-the-art的SuperDepth 网络预测输入图像中逐像素的深度值。然后将FPN网络输出的特征与深度特征堆积在一起,使用带有Group Normalization 的两个卷基层处理得到融合特征,最后使用检测到的2D bbox和ROI Align在ROI Lifting中提取对应的特征,回归3D旋转、平移、目标的绝对尺度以及目标形状。
3.2 由单目2D实例到6D位姿
该问题其实是一个可微分的提升映射, F : R 4 → R 8 × 3 \mathcal{F}: \mathbb{R}^4\rightarrow \mathbb{R}^{8\times 3} F:R4→R8×3,即从一个2D的ROI X \mathcal{X} X到一个3D的bounding box B : = { B 1 , … , B 8 } \mathcal{B}:=\{B_1, \dots, B_8\} B:={B1,…,B8}。将旋转编码为4D的四元数,将平移编码为2D物体中心的相对深度。此外,使用到数据集平均体积的偏差描述物体三维体积。
给定一个2D ROI X \mathcal{X} X,使用ROIAlign提取指定区域特征,分别预测出旋转量 q q q、相对于ROI的2D中心 ( x , y ) (x, y) (x,y)、深度值 z z z和物体的绝对尺度 ( w , h , l ) (w, h, l) (w,h,l),提升映射为:
B i : = q ⋅ ( ± w / 2 ± h / 2 ± l / 2 ) ⋅ q − 1 + K − 1 ( x ⋅ z y ⋅ z z ) B_i :=q\cdot \begin{pmatrix} \pm w/2\\ \pm h/2\\ \pm l/2 \end{pmatrix}\cdot q^{-1} + K^{-1} \begin{pmatrix} x\cdot z\\ y\cdot z\\ z \end{pmatrix} Bi:=q⋅⎝⎛±w/2±h/2±l/2⎠⎞⋅q−1+K−1⎝⎛x⋅zy⋅zz⎠⎞
其中 K K K为相机内参矩阵
损失函数
当仅从单目图像中估计位姿参数时,像素空间中的微小误差可以导致位姿参数的剧烈变化。我们将问题提升到了3D,并使用了6D自由度的代理损失函数。因此,没有同时对所有预测项进行优化,而是让网络在训练期间自己调整。给定一个3D bbox B ∗ : = { B 1 ∗ , … , B 8 ∗ } \mathcal{B^*}:=\{B^*_1, \dots, B^*_8\} B∗:={B1∗,…,B8∗}和对应的2D检测框 X \mathcal{X} X,其到3D的提升映射为 F \mathcal{F} F,在度量空间关于八个3D角点的损失函数为:
L ( F ( X ) , B ∗ ) = 1 8 ∑ i = 1 8 ∥ F ( X ) i − B i ∗ ∥ \mathcal{L}(\mathcal{F}(\mathcal{X}), \mathcal{B}^*)=\frac{1}{8}\sum_{i=1}^8\|\mathcal{F}(X)_i-\mathcal{B}^*_i\| L(F(X),B∗)=81i=1∑8∥F(X)i−Bi∗∥

在训练过程中,需要一个warm up过程以得到稳定的数值流形。因此训练单个的预测项,直到得到稳定的3D box实例。
Allocentric 回归 and Egocentric 提升
相机光轴是否对准目标中心,Egocentric 以相机为中心,相机光轴不一定对准目标中心,allocentric是以目标为中心。两者的区别在于当发生与相机之间的位移时,Allocentric中相机光轴随着目标位移而移动,目标的形状变化不大,而Egocentric中相机光轴不变,目标的形状变化较大。
大视场条件下,Allocentric pose estimation很重要。(Allocentric Pose Estimation. ICCV 2013.)

由于ROI缺少全局的信息,在回归时认为四元数是Allocentric的,然后结合推理出来的平移量矫正为Egocentric,然后提升到3D boxes。
3.3 目标形状学习与检索
介绍了如何将端到端的单目3D目标检测模型扩展到预测三角面片,并用于数据增强。
学习一个光滑的形状
给定了50种商用模型,我们创建了一个映射受限的带符号的距离场(TSDF) ϕ i \phi_i ϕi,大小为 128 × 128 × 256 128\times 128\times 256 128×128×256。首先使用PCA学习低维的形状,实验中发现形状空间很快地偏离了均值。使用PCA生成形状要求评价每一维度的标准差。因此,我们使用一个3D自编码/解码器 E E E和 D \mathcal{D} D,对输出的TSDF强制不同的约束。 E E E和 D \mathcal{D} D都使用了1,8, 16, 32四种卷基层。此外我们使用核为6的全卷积层作为隐藏层。在训练过程中将所有的隐藏层映射到半球上,以保证连续性。对输出层的跳跃通过总方差进行惩罚,损失函数为:
L ( E , D , ϕ ) = ∣ D ( E ( ϕ ) − ϕ ) ∣ + ∣ ∥ E ( ϕ ) ∥ − 1 ∣ + ∣ ▽ D ( E ( ϕ ) ∣ \mathcal{L}(E, D, \phi) = |\mathcal{D}(E(\phi)-\phi)|+|\|E(\phi)\|-1|+|\triangledown \mathcal{D}(E(\phi)| L(E,D,ϕ)=∣D(E(ϕ)−ϕ)∣+∣∥E(ϕ)∥−1∣+∣▽D(E(ϕ)∣
形状真值的标注
对于3D 提升器的形状分支,预测形状 s s s和形状真值 s ∗ s^* s∗间的相似度由两点在半球上的角度决定:
L s h a p e ( s , s ∗ ) = arccos ( ⟨ s , s ∗ ⟩ 2 − 1 ) \mathcal{L}_{shape}(s, s^*)=\arccos(\langle s, s^*\rangle^2 -1) Lshape(s,s∗)=arccos(⟨s,s∗⟩2−1)
在推理时,我们预测了低维的隐藏层向量,并将其传递给解码器以得到TSDF表示。
简单面片纹理
模型可以得到目标的尺度与形状,可以投影检索得到的3D面片。我们将朝向相机的定点映射到图像平面,并赋予相应的值。
3.4 仿真3D 数据增强
KITTI3D数据集较小,且3D真值获取耗时耗力,采用仿真数据是一种常用方法。文章使用提取得到的面片以生成真实的渲染,而不是写固定的CAD模型。此外,仿真目标的摆放没有太多限制。使用allocentric pose移动目标,不改变视角。