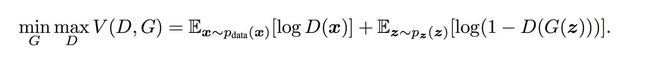淦?GAN!一文搞懂生成对抗网络的思想(文末附基于PaddlePaddle的手写数字生成案例)

最参加了百度顶会论文复现营,经过一个星期的学习,我学到了很多知识,因此我打算把学到的内容好好整理整理,也就有了这篇文章。

点击链接加入课程:
https://aistudio.baidu.com/aistudio/education/group/info/1340

1. 什么是GAN?
2. GAN的基本原理
3. GAN的应用场景
4. 基于飞桨的手写数字生成案例

1. 什么是GAN?

GAN的全拼是GenerativeAdversarialNetworks,翻译过来就是生成对抗网络

换句话说就是通过对抗的方式去学习数据分布的生成式模型

GAN的核心思想是通过 生成网络G (Generator) 和 判别网络D (Discriminator) 不断博弈，来达到生成类真数据的目的

类比监督学习来了解GAN

GAN其实是非监督学习,相较于有标签的监督学习来说,非监督学习对机器来说,没有一个所谓的标准答案。

非监督学习的一个典型案例是鸢尾花分类,机器可以在海量的数据中根据鸢尾花的特征(花萼、花瓣的大小),最后将鸢尾花细分成3个不同的品种:

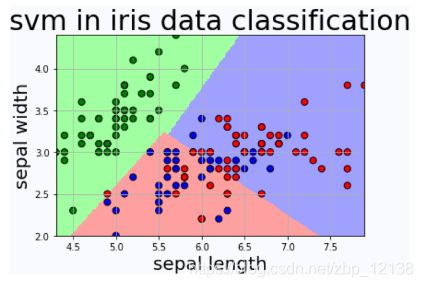
GAN也是类似的,它也没有一个确定的标签,只能通过数据去寻找特征,不过不一样的地方就在于,GAN是对抗式的,这里举个例子吧:

比如钞票和验钞机。验钞机要做的就是验出钞票的真伪,而有些不法分子就妄想着做假钞来骗过验钞机。GAN网络里就有这样的结构,生成网络G就像是不法分子,做假钞;而判别网络D就像是验钞机,判断钞票的真假。这其中就有对抗,当钞票做的越来越真实时,验钞机也要提高自己的辨别能力,换句话说,这种对抗是一个持续的过程,一方变强时,另一方要变得更强。我们期望对抗的最终结果是达到一个纳什均衡点。

类比强化学习来了解GAN

强化学习中,也有类似的结构即Actor-Critic,演员-评论家结构。

有所不同的是,AC结构是一种类似合作的关系,它不存在所谓的竞争。就像是足球场上的球员和教练,教练指导球员做动作,从而让球员拿高分。

而生成对抗网络是一个存在竞争关系的网络结构,没有合作,就像上面那个钞票和验钞机的例子,这两者本身就是竞争关系,不能存在合作的关系。

2. GAN的基本原理

在讲原理之前,先来看看GAN的发展脉络:

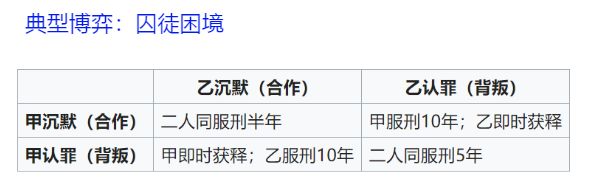
GAN 的思想启发自博弈论中的零和游戏

零和游戏指参与博弈的各方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加总和永远为“零”，双方不存在合作的可能。

纳什均衡

纳什均衡是指博弈中这样的局面，对于每个参与者来说，只要其他人不改变策略，他就无法改善自己的状况。

在一个博弈过程中，无论对方的策略选择如何，当事人一方都会选择某个确定的策略，则该策略被称作支配性策略。如果任意一位参与者在其他所有参与者的策略确定的情况下，其选择的策略是最优的，那么这个组合就被定义为纳什平衡即纳什均衡点。

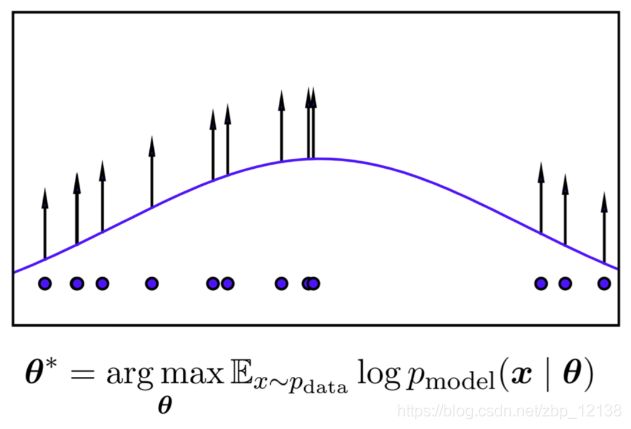
最大似然估计

在统计学中，最大似然估计（Maximum Likelihood Estimation，缩写为MLE），也称最大概似估计，是用来估计一个概率模型的参数的一种方法

就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值

GAN的原理概述

GAN 的思想就启发自博弈论中的零和游戏，它包含一个生成网络G和一个判别网络D

• G是一个生成式的网络，它接收一个随机的噪声Z，通过Generator生成假数据Xfake
• D是一个判别网络，判别输入数据的真实性。它的输入是X，输出D(X)代表X为真实数据的概率
• 训练过程中，生成网络G的目标是尽量生成真实的数据去欺骗判别网络D。而D的目标就是尽量辨别出G生成的假数据和真数据。这个博弈过程最终的平衡点是纳什均衡点。

从更具体的例子看GAN原理

假设我们有两个网络，G和D。

• G是一个生成图片的网络，它接收一个随机的噪声z，通过这个噪声生成图片，记做G(z)
• D是一个判别网络，判别一张图片是不是“真实的”。它的输入x代表一张图片，输出D(x)代表x为真实图片的概率:
  如果输出为1，就代表100%是真实的图片;
  而输出为0，就代表不可能是真实的图片。

在训练过程中，生成网络G的目标就是尽量生成真实的图片去欺骗判别网络D。而D的目标就是尽量把G生成的图片和真实的图片分别开来。这样，G和D构成了一个动态的“博弈过程”。

最后博弈的结果是什么？在最理想的状态下，G可以生成足以“以假乱真”的图片G(z)。对于D来说，它难以判定G生成的图片究竟是不是真实的，因此D(G(z)) = 0.5。

GAN的目标函数

• x表示真实图片，z表示输入G网络的噪声，而G(z)表示G网络生成的数据。
• D(x)表示D网络判断真实数据是否真实的概率，而D(G(z))是D网络判断G生成的数据是否真实的概率。
• G的目的：G希望自己生成的数据“越接近真实越好”。也就是说，G希望D(G(z))尽可能得大，这时V(D, G)会变小。因此我们看到式子的最前面的记号是min G。
• D的目的：D的能力越强，D(x)应该越大，D(G(x))应该越小。这时V(D,G)会变大。因此式子对于D来说是求最大(max D)

GAN的训练方法

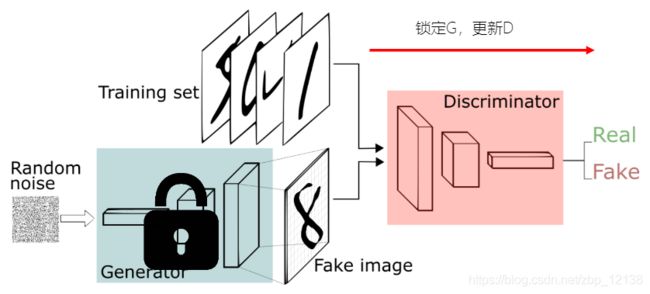
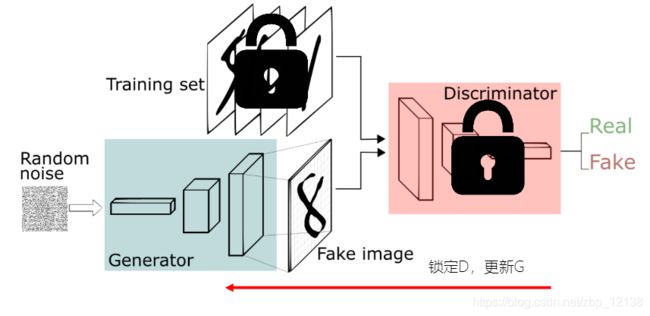
GAN里有两个网络,分别是G网络和D网络,两个都需要训练，而且彼此依赖,这时我们可以分开训练:

• 先锁定G网络,更新D网络
  
• 然后锁定D网络,更新G网络
  

GAN的训练细节

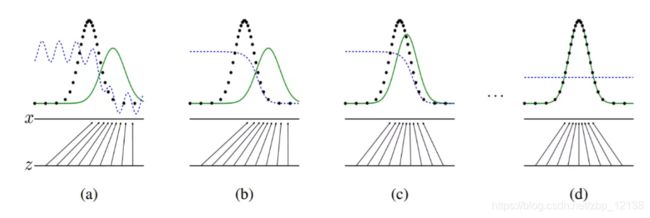
GAN的训练可视化

• 虚线点为真实的数据分布，蓝色虚线是判别器，绿色实线为生成器。
• 由左至右可以看到生成的分布越来越接近真实分布，而判别器的概率最后变为0.5

GAN的优点

GAN存在的问题

不收敛

训练GAN需要达到纳什均衡,有时候可以用梯度下降法做到,有时候做不到.我们还没有找到很好的达到纳什均衡的方法,所以训练GAN相比VAE是不稳定的:

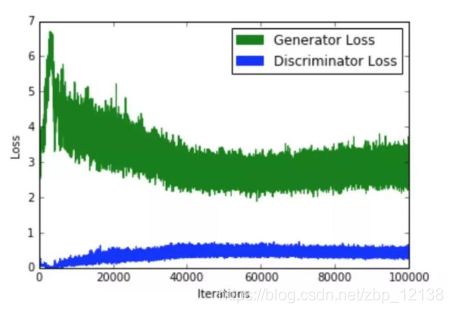
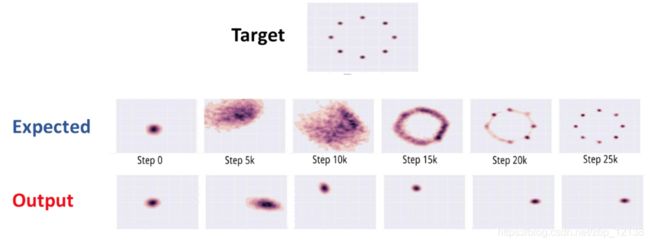
模式坍塌

模式坍塌可以理解为生成的内容没有多样性,一般出现在GAN训练不稳定的时候，具体表现为生成出来的结果非常差，但是即使加长训练时间后也无法得到很好的改善。

模式坍塌的原因

• GAN采用的是对抗训练的方式，G的梯度更新来自D，所以G生成的好不好，依赖于D的评价。
• 如果某一次G生成的样本可能并不是很好，但是D给出了很好的评价，或者是G生成的结果中一些特征得到了D的认可，这时候G就会认为我输出的正确的，那么接下来我就这样输出肯定D还会给出比较高的评价（实际上G生成的并不好）
• 进入一种“死循环”，最终生成结果缺失一些信息，特征不全。

模式坍塌的解决方案

针对目标函数的改进方法

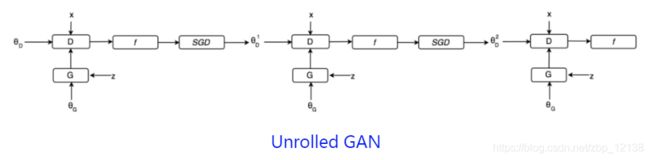
为了避免前面提到的由于优化maxmin导致mode 跳来跳去的问题，UnrolledGAN采用修改生成器loss 来解决。具体而言，UnrolledGAN在更新生成器时更新k 次生成器，参考的Loss 不是某一次的loss，是判别器后面k 次迭代的loss。

注意，判别器后面k 次迭代不更新自己的参数，只计算loss 用于更新生成器。这种方式使得生成器考虑到了后面k 次判别器的变化情况，避免在不同mode 之间切换导致的模式崩溃问题。

针对网络结构的改进方法(1)

Multi agent diverse GAN (MAD-GAN) 采用多个生成器，一个判别器以保障样本生成的多样性。

相比于普通GAN，多了几个生成器，且在loss 设计的时候，加入一个正则项。正则项使用余弦距离惩罚三个生成器生成样本的一致性。

针对网络结构的改进方法(2)

• MRGAN 则添加了一个判别器来惩罚生成样本的mode collapse 问题
• 输入样本x 通过一个Encoder 编码为隐变量E(x) ，然后隐变量被Generator 重构，训练时有三个loss
• $D_M$和R （重构误差）用于指导生成real-like 的样本。而$D_D$则对E(x) 和z 生成的样本进行判别

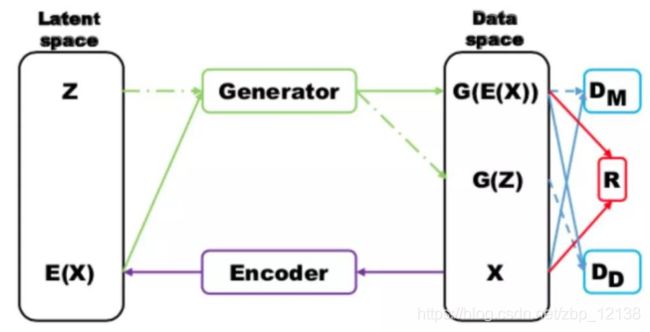
显然二者生成样本都是fake samples，所以这个判别器主要用于判断生成的样本是否具有多样性，即是否出现mode collapse。

GAN常见的模型结构

DeepConvolutionalGAN(DCGAN)

核心思想:

1. 使用卷积层替换全连接层
2. 在每层后使用BatchNormalization。将特征层的输出归一化到一起，加速了训练，提升了训练的稳定性。（生成器的最后一层和判别器的第一层不加batchnorm）
3. G的隐藏层使用ReLU；G的输出层使用Tanh；D使用leakrelu激活函数，而不是RELU，防止梯度稀疏

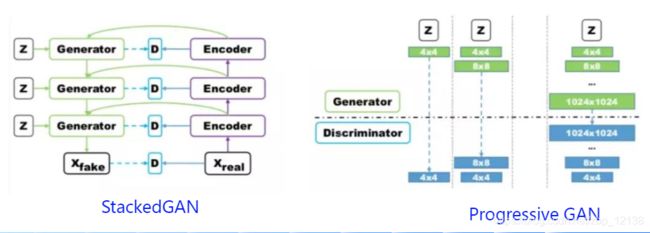
层级结构

GAN 对于高分辨率图像生成一直存在许多问题，层级结构的GAN 通过逐层次，分阶段生成，一步步提生图像的分辨率。典型的使用多对GAN 的模型有StackGAN，GoGAN。使用单一GAN，分阶段生成的有ProgressiveGAN

自编码结构

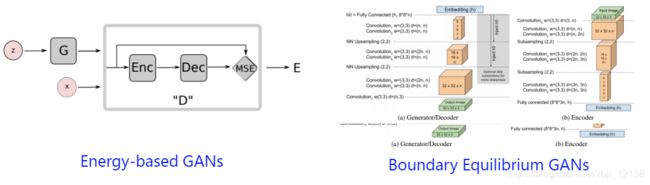
经典的GAN 结构里面，判别网络通常被当做一种用于区分真实/生成样本的概率模型。而在自编码器结构里面，判别器（使用AE 作为判别器）通常被当做能量函数（Energy function）。

对于离数据流形空间比较近的样本，其能量较小，反之则大。有了这种距离度量方式，自然就可以使用判别器去指导生成器的学习。典型的自编码器结构的GAN 有：BEGAN，EBGAN，MAGAN 等。

3. GAN的应用场景

GAN的潜力巨大，因为它们能去学习模仿任何数据分布，因此，GANs能被教导在任何领域创造类似于我们的世界，比如图像、音乐、演讲、散文。在某种意义上，他们是机器人艺术家，他们的输出令人印象深刻，甚至能够深刻的打动人们。

4. 基于飞桨的手写数字生成案例

任务描述

GAN全称是 Generative Adversarial Network，即生成对抗网络。在14年被Goodfellow等提出后即热度不断一经推出便引爆全场，此后各种花式变体DCGAN、WGAN、CGAN、CYCLEGAN、STARGAN、LSGAN等层出不穷，在“换脸”、“换衣”、“换天地”等应用场景下生成的图像、视频以假乱真，好不热闹。

生成对抗网络一般由一个生成器（生成网络），和一个判别器（判别网络）组成。

生成器的作用是，通过学习训练集数据的特征，在判别器的指导下，将随机噪声分布尽量拟合为训练数据的真实分布，从而生成具有训练集特征的相似数据。而判别器则负责区分输入的数据是真实的还是生成器生成的假数据，并反馈给生成器。两个网络交替训练，能力同步提高，直到生成网络生成的数据能够以假乱真，并与与判别网络的能力达到一定均衡。

数据准备

训练集数据使用飞桨框架内置函数paddle.dataset.mnist.train()、paddle.reader.shuffle()和paddle.batch()进行读取、打乱和划分batch。读取图片数据处理为 [N,W,H] 格式。

要喂入生成器高斯分布的噪声隐变量z的维度设置为100。

import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph import Conv2D, Pool2D, Linear
import numpy as np
import matplotlib.pyplot as plt

# 噪声维度
Z_DIM = 100
BATCH_SIZE = 128
# 读取真实图片的数据集，这里去除了数据集中的label数据，因为label在这里使用不上，这里不考虑标签分类问题。
def mnist_reader(reader):
    def r():
        for img, label in reader():
            yield img.reshape(1, 28, 28)
    return r

# 噪声生成，通过由噪声来生成假的图片数据输入。
def z_reader():
    while True:
        yield np.random.normal(0.0, 1.0, (Z_DIM, 1, 1)).astype('float32')                #正态分布，正态分布的均值、标准差、参数

# 生成真实图片reader
mnist_generator = paddle.batch(
        paddle.reader.shuffle(mnist_reader(paddle.dataset.mnist.train()), 30000),
        batch_size=BATCH_SIZE)

# 生成假图片的reader
z_generator = paddle.batch(z_reader, batch_size=BATCH_SIZE)

测试下数据读取器和高斯噪声生成器:

import matplotlib.pyplot as plt
%matplotlib inline

pics_tmp = next(mnist_generator())
print('一个batch图片数据的形状：batch_size =', len(pics_tmp), ', data_shape =', pics_tmp[0].shape)

plt.imshow(pics_tmp[0][0]) # (28,28)
plt.show

z_tmp = next(z_generator())
print('一个batch噪声z的形状：batch_size =', len(z_tmp), ', data_shape =', z_tmp[0].shape)

GAN网络

GAN性能的提升从生成器G和判别器D进行左右互搏、交替完善的过程得到的。所以其G网络和D网络的能力应该设计得相近，复杂度也差不多。这个项目中的生成器，采用了两个全链接层接两组上采样和转置卷积层，将输入的噪声Z逐渐转化为1×28×28的单通道图片输出。

• 生成器结构：
  

class G(fluid.dygraph.Layer):
    def __init__(self, name_scope):
        super(G, self).__init__(name_scope)
        name_scope = self.full_name
        self.fc1 = Linear(input_dim=100, output_dim=1024)
        self.bn1 = fluid.dygraph.BatchNorm(num_channels=1024, act='tanh')
        self.fc2 = Linear(input_dim=1024, output_dim=128*7*7)
        self.bn2 = fluid.dygraph.BatchNorm(num_channels=128*7*7, act='tanh')
        self.conv1 = Conv2D(num_channels=128, num_filters=64, filter_size=5, padding=2)
        self.bn3 = fluid.dygraph.BatchNorm(num_channels=64, act='tanh')
        self.conv2 = Conv2D(num_channels=64, num_filters=1, filter_size=5, padding=2, act='tanh')

    def forward(self, z):
        z = fluid.layers.reshape(z, shape=[-1, 100])
        y = self.fc1(z)
        y = self.bn1(y)
        y = self.fc2(y)
        y = self.bn2(y)
        y = fluid.layers.reshape(y, shape=[-1, 128, 7, 7])
        y = fluid.layers.image_resize(y, scale=2)
        y = self.conv1(y)
        y = self.bn3(y)
        y = fluid.layers.image_resize(y, scale=2)
        y = self.conv2(y)
        return y

判别器的结构正好相反，先通过两组卷积和池化层将输入的图片转化为越来越小的特征图，再经过两层全链接层，输出图片是真是假的二分类结果。

• 判别器结构：
  

class D(fluid.dygraph.Layer):
    def __init__(self, name_scope):
        super(D, self).__init__(name_scope)
        name_scope = self.full_name()
        self.conv1 = Conv2D(num_channels=1, num_filters=64, filter_size=3)
        self.bn1 = fluid.dygraph.BatchNorm(num_channels=64, act='relu')
        self.pool1 = Pool2D(pool_size=2, pool_stride=2)

        self.conv2 = Conv2D(num_channels=64, num_filters=128, filter_size=3)
        self.bn2 = fluid.dygraph.BatchNorm(num_channels=128, act='relu')
        self.pool2 = Pool2D(pool_size=2, pool_stride=2)

        self.fc1 = Linear(input_dim=128*5*5, output_dim=1024)
        self.bnfc1 = fluid.dygraph.BatchNorm(num_channels=1024, act='relu')
        self.fc2 = Linear(input_dim=1024, output_dim=1)

    def forward(self, img):
        y = self.conv1(img)
        y = self.bn1(y)
        y = self.pool1(y)
        y = self.conv2(y)
        y = self.bn2(y)
        y = self.pool2(y)
        y = fluid.layers.reshape(y, shape=[-1,128*5*5])
        y = self.fc1(y)
        y = self.bnfc1(y)
        y = self.fc2(y)
        return y

测试生成器G网络和判别器D网络的前向计算结果。一个batch的数据，输出一张图片。

# 测试生成网络G和判别网络D
with fluid.dygraph.guard():
    g_tmp = G('G')
    tmp_g = g_tmp(fluid.dygraph.to_variable(np.array(z_tmp))).numpy()
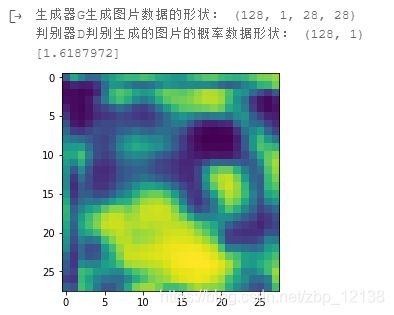
    print('生成器G生成图片数据的形状：', tmp_g.shape)
    plt.imshow(tmp_g[0][0])
    plt.show()
    
    d_tmp = D('D')
    tmp_d = d_tmp(fluid.dygraph.to_variable(tmp_g)).numpy()
    print('判别器D判别生成的图片的概率数据形状：', tmp_d.shape)
    print(max(tmp_d))

# 显示图片，构建一个16*n大小(n=batch_size/16)的图片阵列，把预测的图片打印到note中。
import matplotlib.pyplot as plt
%matplotlib inline

def show_image_grid(images, batch_size=128, pass_id=None):
    fig = plt.figure(figsize=(8, batch_size/32))
    fig.suptitle("Pass {}".format(pass_id))
    gs = plt.GridSpec(int(batch_size/16), 16)
    gs.update(wspace=0.05, hspace=0.05)

    for i, image in enumerate(images):
        ax = plt.subplot(gs[i])
        plt.axis('off')
        ax.set_xticklabels([])
        ax.set_yticklabels([])
        ax.set_aspect('equal')
        plt.imshow(image[0], cmap='Greys_r')    
    plt.show()

show_image_grid(tmp_g, BATCH_SIZE)

网络训练

网络的训练优化目标就是如下公式：

公式出自Goodfellow在2014年发表的论文Generative Adversarial Nets。
这里简单介绍下公式的含义和如何应用到代码中。

下面是训练模型的代码，有详细的注释。大致过程是：先用真图片训练一次判别器d的参数，再用生成器g生成的假图片训练一次判别器d的参数，最后用判别器d判断生成器g生成的假图片的概率值更新一次生成器g的参数，即每轮训练先训练两次判别器d，再训练一次生成器g，使得判别器d的能力始终稍稍高于生成器g一些。

def train(mnist_generator, epoch_num=1, batch_size=128, use_gpu=True, load_model=False):
    place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
    with fluid.dygraph.guard(place):
        # 模型存储路径
        model_path = './output/'
        d = D('D')
        d.train()
        g = G('G')
        g.train()
        # 创建优化方法
        real_d_optimizer = fluid.optimizer.AdamOptimizer(learning_rate=2e-4, parameter_list=d.parameters())
        fake_d_optimizer = fluid.optimizer.AdamOptimizer(learning_rate=2e-4, parameter_list=d.parameters())
        g_optimizer = fluid.optimizer.AdamOptimizer(learning_rate=2e-4, parameter_list=g.parameters())
        
        # 读取上次保存的模型
        if load_model == True:
            g_para, g_opt = fluid.load_dygraph(model_path+'g')
            d_para, d_r_opt = fluid.load_dygraph(model_path+'d_o_r')
            # 上面判别器的参数已经读取到d_para了,此处无需再次读取
            _, d_f_opt = fluid.load_dygraph(model_path+'d_o_f')
            g.load_dict(g_para)
            g_optimizer.set_dict(g_opt)
            d.load_dict(d_para)
            real_d_optimizer.set_dict(d_r_opt)
            fake_d_optimizer.set_dict(d_f_opt)

        iteration_num = 0
        for epoch in range(epoch_num):
            for i, real_image in enumerate(mnist_generator()):
                # 丢弃不满整个batch_size的数据
                if(len(real_image) != BATCH_SIZE):
                    continue               
                iteration_num += 1                
                '''
                判别器d通过最小化输入真实图片时判别器d的输出与真值标签ones的交叉熵损失，来优化判别器的参数，
                以增加判别器d识别真实图片real_image为真值标签ones的概率。
                '''
                # 将MNIST数据集里的图片读入real_image，将真值标签ones用数字1初始化
                real_image = fluid.dygraph.to_variable(np.array(real_image))
                ones = fluid.dygraph.to_variable(np.ones([len(real_image), 1]).astype('float32'))
                # 计算判别器d判断真实图片的概率
                p_real = d(real_image)
                # 计算判别真图片为真的损失
                real_cost = fluid.layers.sigmoid_cross_entropy_with_logits(p_real, ones)
                real_avg_cost = fluid.layers.mean(real_cost)
                # 反向传播更新判别器d的参数
                real_avg_cost.backward()
                real_d_optimizer.minimize(real_avg_cost)
                d.clear_gradients()
                
                '''
                判别器d通过最小化输入生成器g生成的假图片g(z)时判别器的输出与假值标签zeros的交叉熵损失，
                来优化判别器d的参数，以增加判别器d识别生成器g生成的假图片g(z)为假值标签zeros的概率。
                '''
                # 创建高斯分布的噪声z，将假值标签zeros初始化为0
                z = next(z_generator())
                z = fluid.dygraph.to_variable(np.array(z))
                zeros = fluid.dygraph.to_variable(np.zeros([len(real_image), 1]).astype('float32'))
                # 判别器d判断生成器g生成的假图片的概率
                p_fake = d(g(z))
                # 计算判别生成器g生成的假图片为假的损失
                fake_cost = fluid.layers.sigmoid_cross_entropy_with_logits(p_fake, zeros)
                fake_avg_cost = fluid.layers.mean(fake_cost)
                # 反向传播更新判别器d的参数
                fake_avg_cost.backward()
                fake_d_optimizer.minimize(fake_avg_cost)
                d.clear_gradients()

                '''
                生成器g通过最小化判别器d判别生成器生成的假图片g(z)为真的概率d(fake)与真值标签ones的交叉熵损失，
                来优化生成器g的参数，以增加生成器g使判别器d判别其生成的假图片g(z)为真值标签ones的概率。
                '''
                # 生成器用输入的高斯噪声z生成假图片
                fake = g(z)
                # 计算判别器d判断生成器g生成的假图片的概率
                p_confused = d(fake)
                # 使用判别器d判断生成器g生成的假图片的概率与真值ones的交叉熵计算损失
                g_cost = fluid.layers.sigmoid_cross_entropy_with_logits(p_confused, ones)
                g_avg_cost = fluid.layers.mean(g_cost)
                # 反向传播更新生成器g的参数
                g_avg_cost.backward()
                g_optimizer.minimize(g_avg_cost)
                g.clear_gradients()
                
                # 打印输出
                if(iteration_num % 200 == 0):
                    print('epoch =', epoch, ', batch =', i, ', real_d_loss =', real_avg_cost.numpy(),
                     ', fake_d_loss =', fake_avg_cost.numpy(), 'g_loss =', g_avg_cost.numpy())
                    show_image_grid(fake.numpy(), BATCH_SIZE, epoch)                             
        
        # 存储模型
        fluid.save_dygraph(g.state_dict(), model_path+'g')
        fluid.save_dygraph(g_optimizer.state_dict(), model_path+'g')
        fluid.save_dygraph(d.state_dict(), model_path+'d_o_r')
        fluid.save_dygraph(real_d_optimizer.state_dict(), model_path+'d_o_r')
        fluid.save_dygraph(d.state_dict(), model_path+'d_o_f')
        fluid.save_dygraph(fake_d_optimizer.state_dict(), model_path+'d_o_f')

train(mnist_generator, epoch_num=100, batch_size=64, use_gpu=True)

训练效果: