【学习笔记】Pytorch深度学习—损失函数(一)
【学习笔记】Pytorch深度学习—损失函数(一)
- 损失函数概念
- 交叉熵损失函数
- 其他损失函数NLL、BCE、BCEWithLogits Loss
前面学习了如何构建模型、模型初始化,本章学习损失函数。本章从3个方面学习,(1)损失函数的概念以及作用;(2)学习交叉熵损失函数;(3)学习其他损失函数NLL、BCE、BCEWithLogits Loss
损失函数概念
损失函数:衡量模型输出与真实标签的差异。

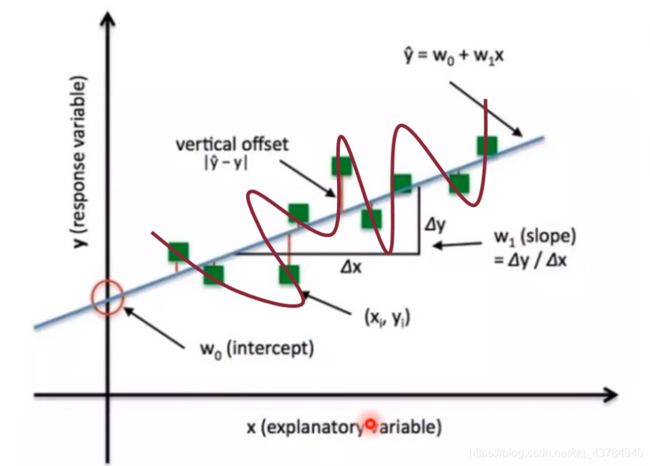
如图1所示,一元线性回归模型中绿色点是训练样本,蓝色曲线是训练好的模型,从图中可以看出,该模型并未完全拟合到每1个数据点,即未能使得所有数据点都在模型上,因此,数据点产生了Loss。如第5个数据点,模型输出与真实输出产生了差异,这里采用了绝对值损失函数 ∣ y ^ − y ∣ \vert \hat{y}-y\vert ∣y^−y∣ 来衡量模型输出与真实标签之前的差异。
通常,说到损失函数会出现3个概念:
(1)损失函数(Loss Function):计算单样本的差异
L o s s = f ( y ^ , y ) Loss=f(\hat{y},y) Loss=f(y^,y)
(2)代价函数(Cost Function):计算整个训练集、样本集(所有样本)Loss的平均值
C o s t = 1 N ∑ i N f ( y i ^ , y i ) Cost=\frac{1}{N} \sum_{i}^N f(\hat{y_i},y_i) Cost=N1i∑Nf(yi^,yi)
(3)目标函数(Objective Function):训练模型的最终目标—目标包含cost和Regularization
O b j = C o s t + R e g u l a r i z a t i o n T e r m Obj=Cost+Regularization \quad Term Obj=Cost+RegularizationTerm
①Cost代价函数衡量模型输出与真实标签之间的差异,即要求模型输出与真实标签之间的差异要尽量小。那么,是不是模型输出与真实标签之间的差异越小越好呢? 其实,并不一定,因为有时候可能会造成模型过拟合。
如图2,模型完全拟合了每个数据点,代价函数Cost为0,但却不是1个好的模型,模型太复杂而造成过拟合。
②正则项Regularization Term:在追求模型输出与真实标签之间差异较小时,同时也要对模型做出限制、约束(抑制过拟合),这些约束项就称之为正则项。通常采用L1、L2加在Cost项之后,构成目标函数。
后文,不失一般性,用损失函数Loss Function代替代价函数Cost Function。衡量模型输出与真实标签之间差异统称为Loss Function。
交叉熵损失函数
Pytorch中交叉熵损失函数的实现
1、nn.CrossEntropyLoss
nn.CrossEntropyLoss
功能:nn.LogSoftmax()与nn.NLLLoss()结合,进行交叉熵计算
将nn模块中的Logsoftmax激活函数与NLL结合,这一函数并不是公式意义上的交叉熵函数计算,不同之处在于,它采用了softmax对数据进行了归一化:将数据值归一化到概率输出的区间。这是因为交叉熵函数常用于分类任务中,分类任务通常需要计算两个输出的概率值,交叉熵衡量两个概率分布之间的差异。交叉熵值越低,两个分布越相似。
1.1 分析
①交叉熵

观察上述公式, P P P是训练集中样本真实概率分布, Q Q Q是模型输出分布,机器学习模型中优化、最小化交叉熵等价于优化相对熵。由于训练集是固定,P的信息熵 H ( P ) H(P) H(P)是常数,在优化时常数可忽略,因此,优化交叉熵则等价于优化相对熵。
②Logsoftmax函数
softmax可以将输出数据值可以归一到概率区间,再根据Log、NLLLoss计算交叉熵。
H ( P , Q ) = − ∑ i N P ( x i ) l o g Q ( x i ) H(P,Q)=-\sum_i^NP(x_i)logQ(x_i) H(P,Q)=−i∑NP(xi)logQ(xi)
l o s s ( x , c l a s s ) = − l o g ( e x p ( x [ c l a s s ] ) ∑ j e x p ( x [ j ] ) ) = − x [ c l a s s ] + l o g ( ∑ j e x p ( x [ j ] ) ) loss(x,class)=-log(\frac{exp(x[class])}{\sum_jexp(x[j])})=-x[class]+log(\sum_jexp(x[j])) loss(x,class)=−log(∑jexp(x[j])exp(x[class]))=−x[class]+log(j∑exp(x[j]))

在没有weight权值时,接收输出概率值x、class类别值,然后对其取指数exp即softmax,在取-log即得到交叉熵损失函数(这里计算时取了某1个样本,故 P ( x i ) P(x_i) P(xi)=1)
nn.CrossEntropyLoss主要参数
nn.CrossEntropyLoss(weight=None,
size_average=None,
ignore_index=-100,
reduce=None,
reduction='mean')
功能:nn.LogSoftmax()与nn.NLLLoss()结合,进行交叉熵计算
主要参数:
weight:各个类别的Loss设置权值
ignore_index:忽略某个类别
reduction:计算模式可为none/sum/mean
none-逐个元素计算
sum-所有元素求和,返回标量
mean-加权平均,返回标量
解释
(1)weight:为各个类别的Loss设置权值
l o s s ( x , c l a s s ) = w e i g h t [ c l a s s ] ( − x [ c l a s s ] + l o g ( ∑ j e x p ( x [ j ] ) ) ) loss(x,class)=weight[class](-x[class]+log(\sum_jexp(x[j]))) loss(x,class)=weight[class](−x[class]+log(j∑exp(x[j])))比如,想让第0类的Loss更大一些,模型更关注第0类,可以设置该类别的权值weight=1.2,可以使得Loss被放大1.2倍。
(2)ignore_index:用来指示某个类别不计算Loss。例如1000类分类任务中,不想计算第999类的Loss,即可设置ignore_index=999;
(3)reduction:用来计算Loss的模型,具体有3类none/sum/mean。 none逐个样本计算Loss,有多少个独立样本,就返回多少个Loss;sum、mean均返回标量。
(4)现在函数中仍存在的size_average和reduce在早期是用来设定计算模式的,现已通过reduction来设置。
1.2 实验
1.2.1 通过实验认识CrossEntropyLoss交叉熵的不同计算模式reduction
3个样本分别是输入输出神经元,即第1个样本输入为1,输出值为3,第2个样本输入为1,输出为3,第3个样本输入为1,输出为3。
//构建虚拟数据 batch_size=3即3个样本
inputs = torch.tensor([[1, 2], [1, 3], [1, 3]], dtype=torch.float)
//设置标签、类型为长整型,第1个样本为第0类,第2、3个样本为第1类,注意类别数class是从0算起的
target = torch.tensor([0, 1, 1], dtype=torch.long)
//通过nn.CrossEntropyLoss构造损失函数,观察3种reduction模式下Loss计算
# ----------------------------------- CrossEntropy loss: reduction -----------------------------------
# flag = 0
flag = 1
if flag:
# def loss function
loss_f_none = nn.CrossEntropyLoss(weight=None, reduction='none')//维度上不衰减,有3个样本就有3个Loss
loss_f_sum = nn.CrossEntropyLoss(weight=None, reduction='sum')//求和模式:把所有样本的Loss加起来
loss_f_mean = nn.CrossEntropyLoss(weight=None, reduction='mean')//默认模式-均分
# forward
loss_none = loss_f_none(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)
# view
print("Cross Entropy Loss:\n ", loss_none, loss_sum, loss_mean)
实验结果

1.2.2 通过实验认识CrossEntropyLoss交叉熵中weight参数的作用
# flag = 0
flag = 1
if flag:
# def loss function
//weight设置时需要注意是“向量形式”,有多少个类别就需要设置多长的向量,每个类别都需要设置weight,不想关注的类别可以设置为1.设置weight,不需要关注尺度,只需要关注各类别之间的比例。
//设置第0类权重为1,第1类权重为2
weights = torch.tensor([1, 2], dtype=torch.float)
# weights = torch.tensor([0.7, 0.3], dtype=torch.float)
loss_f_none_w = nn.CrossEntropyLoss(weight=weights, reduction='none')
loss_f_sum = nn.CrossEntropyLoss(weight=weights, reduction='sum')
loss_f_mean = nn.CrossEntropyLoss(weight=weights, reduction='mean')
# forward
loss_none_w = loss_f_none_w(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)
# view
print("\nweights: ", weights)
print(loss_none_w, loss_sum, loss_mean)
实验结果

在带有权值weight模式下求均值不是求样本的个数,而是求样本占的权值份数。
其他损失函数NLL、BCE、BCEWithLogits Loss
一、NLL实现负对数似然函数中负号功能
nn.NLLLoss
nn.NLLLoss
功能:实现负对数似然函数中负号功能
主要参数(与nn.CrossEntropyLoss相似):
weight:各个类别的Loss设置权限
ignore_index:忽略某个类别
reduction:计算模式可为none-逐个元素计算/sum-所有元素求和,返回标量/mean-加权平均,返回标量
实验
# fake data
inputs = torch.tensor([[1, 2], [1, 3], [1, 3]], dtype=torch.float)
target = torch.tensor([0, 1, 1], dtype=torch.long)
flag = 1
if flag:
weights = torch.tensor([1, 1], dtype=torch.float)
loss_f_none_w = nn.NLLLoss(weight=weights, reduction='none')
loss_f_sum = nn.NLLLoss(weight=weights, reduction='sum')
loss_f_mean = nn.NLLLoss(weight=weights, reduction='mean')

二、二分类交叉熵损失函数BCE
它是交叉熵损失函数的特例,BCELoss是真正意义上的(和公式定义上一样的)求取给定inputs和target标签之间的交叉熵。

nn.BCELoss
nn.BCELoss
注意事项:输入输出取值在[0,1]
主要参数(与nn.CrossEntropyLoss相似):
weight:各个类别的Loss设置权限
ignore_index:忽略某个类别
reduction:计算模式可为none-逐个元素计算/sum-所有元素求和,返回标量/mean-加权平均,返回标量
解释:由于交叉熵衡量两个概率分布之间的差异,所以给BCELoss函数输入值取值范围应为[0,1],如果不在这个范围,则会报错。
实验
flag = 1
if flag:
# 虚拟输入:二分类所以有2个神经元,4个样本,第1个样本:第1个神经元输出值为1,第2个神经元输出值为2
inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
# BCE与CrossEntropyLoss的标签不同,是浮点类数据,每个神经元一一对应的计算Loss,而非一整个神经元向量计算Loss
target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)
target_bce = target
weights = torch.tensor([1, 1], dtype=torch.float)
loss_f_none_w = nn.BCELoss(weight=weights, reduction='none')
loss_f_sum = nn.BCELoss(weight=weights, reduction='sum')
loss_f_mean = nn.BCELoss(weight=weights, reduction='mean')
# forward
loss_none_w = loss_f_none_w(inputs, target_bce)
loss_sum = loss_f_sum(inputs, target_bce)
loss_mean = loss_f_mean(inputs, target_bce)
实验结果

输入值并没有在[0,1]之间,由于BCE二分类交叉熵损失函数衡量的是两个概率分布之间的差异,因此输入应当在[0,1]之间。因此,需要将输入值经过激活函数 sigmoid()进行压缩,使其输出值在(0,1)之间。
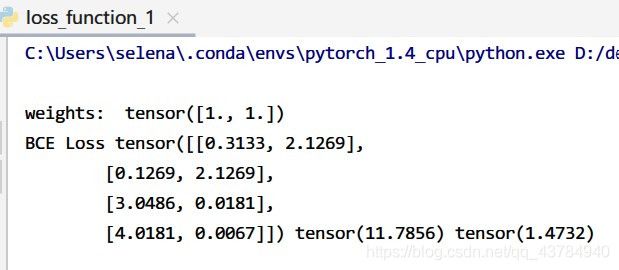
从图中可以看出Loss是8个数值,1个样本有2个神经元,4个样本共计8个神经元,正好也计算了8个Loss。对于每个神经元一一对应计算Loss。总和为8个Loss求和,均分为总和除以8。
三、BCEWithLogits Loss
如果输入不在[0,1]之间,BCELoss就会报错,为此Pytorch专门提供了一种函数BCEWithLogits Loss结合sigmoid函数、BCE二分类交叉熵函数。因此,该损失函数网络的最后一层不能再加sigmoid。由于有时候希望模型最后一层是sigmoid,但是求取Loss又需要输入值在[0,1]区间,因此Pytorch提供了将sigmoid放入到损失函数中的BCEWithLogits Loss。
nn.BCEWithLogits Loss
注意事项:网络最后不加sigmoid函数
主要参数(与nn.CrossEntropyLoss相似):
与其它不同:pos_weight:正样本的权值
weight:各个类别的Loss设置权限
ignore_index:忽略某个类别
reduction:计算模式可为none-逐个元素计算/sum-所有元素求和,返回标量/mean-加权平均,返回标量
解释:pos_weight正样本的权值,该参数用来均衡正负样本,对正样本的Loss乘以该系数。比如,正样本有100个,负样本有300个,正负样本比例1:3;若设置pos_weight=3,对正样本的Loss乘以该系数3,这样等价于正、负样本均有300个,从而实现正负样本的均衡性。
实验
①BCEWithLogits Loss网络最后不加sigmoid
if flag:
inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)
target_bce = target
weights = torch.tensor([1, 1], dtype=torch.float)
loss_f_none_w = nn.BCEWithLogitsLoss(weight=weights, reduction='none')
loss_f_sum = nn.BCEWithLogitsLoss(weight=weights, reduction='sum')
loss_f_mean = nn.BCEWithLogitsLoss(weight=weights, reduction='mean')
# forward
loss_none_w = loss_f_none_w(inputs, target_bce)
loss_sum = loss_f_sum(inputs, target_bce)
loss_mean = loss_f_mean(inputs, target_bce)

②BCEWithLogits Loss网络最后加sigmoid
if flag:
inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)
target_bce = target
inputs = torch.sigmoid(inputs)
weights = torch.tensor([1, 1], dtype=torch.float)
loss_f_none_w = nn.BCEWithLogitsLoss(weight=weights, reduction='none')
loss_f_sum = nn.BCEWithLogitsLoss(weight=weights, reduction='sum')
loss_f_mean = nn.BCEWithLogitsLoss(weight=weights, reduction='mean')
# forward
loss_none_w = loss_f_none_w(inputs, target_bce)
loss_sum = loss_f_sum(inputs, target_bce)
loss_mean = loss_f_mean(inputs, target_bce)
BCEWithLogits Loss本就结合了sigmoid函数,如果在网络后又再一次进行了sigmoid,那么求解得到Loss就是错误结果。
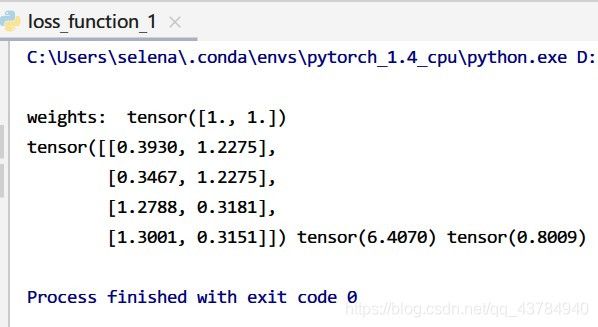
③BCEWithLogits Loss之pos_weight参数
# flag = 0
flag = 1
if flag:
inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)
target_bce = target
# itarget
# inputs = torch.sigmoid(inputs)
weights = torch.tensor([1], dtype=torch.float)
pos_w = torch.tensor([3], dtype=torch.float) # 3
loss_f_none_w = nn.BCEWithLogitsLoss(weight=weights, reduction='none', pos_weight=pos_w)
loss_f_sum = nn.BCEWithLogitsLoss(weight=weights, reduction='sum', pos_weight=pos_w)
loss_f_mean = nn.BCEWithLogitsLoss(weight=weights, reduction='mean', pos_weight=pos_w)
# forward
loss_none_w = loss_f_none_w(inputs, target_bce)
loss_sum = loss_f_sum(inputs, target_bce)
loss_mean = loss_f_mean(inputs, target_bce)
