Nowcoder 5477E. 弦（卡特兰数、组合数学）

题目描述：

给定一个圆，圆上有2N个互不重叠的点。每次操作随机选择两个先前未选择过的点连一条弦，共连成N条弦，求所有弦不交的概率。

输入描述:
一行，只有一个整数N（1≤N≤10^7）。

输出描述:
一行，即答案。答案应以模10 ^ 9+7的形式输出。正式的说，令M=10 ^ 9+7，答案可以表示为最简分数p/q的形式，其中p和q为整数且q与M互质。输出整数x满足 0≤x

示例1
输入

2

输出

666666672

算法标签：卡特兰数、组合数学

首先确定思考方向，要用合法方案/总方案来计算出概率，那么关键在于如何计算合法的方案数。

不妨先将题目中的圆和2N个点，转换为一个正2N边形，这样就得到了一个比较经典的卡特兰数模型，即用不相交的直线连接多边形的顶点，问一共多少种划分方式。

以N=3构成的正六边形为例，可以得到下图的五种合法方案。

怎样来计算合法的方案数呢（令f(N)为2N个结点的合法方案数）。可以以左下角红点为基点，分类讨论与红点相连的结点是哪个。

很明显，合法的连接方法只有三条绿边，因为如果和蓝点相连，正六边形被分割成的两个区域内结点个数都是奇数，一定会发生边相交的情况。

于是依次考虑三条绿边左右两边的连接方案，由于左右区域不可能互相连接（否则与绿边相交）于是可以分别视作两个独立的区域，将各自的方案数相乘，并相加后得到f(3)=f(0)*f(2)+f(1)*f(1)+f(2)*f(0)=1*2+1*1+2*1=5。

将其推广到n的情况，得到这样一个公式：
$$f(n)=\sum _{i=0}^{n-1}f(i)\ast f(n-i-1)$$

这种形式的递推数列即称之为卡特兰数。其相对应的应用还有很多，这里可以展开讨论一下，并尝试找到其本质含义。

比如在一个堆栈中，元素入栈的顺序依次为1、2、3、…、n，问出栈方法总共有多少种？

求解思路依然是一个分类讨论思想。假设最后一个出栈的数为k，那么，将整个过程可以分为四个部分

1. 1、2、3、…、k-1 进栈并按某种顺序出栈
2. k进栈
3. k+1、k+2、…、n进栈，并按某种顺序出栈
4. k出栈

不难发现第一步的方案数为f(k-1)，第三步的方案数为f(n-k)，其乘积f(k-1)*f(n-k)即为“最后一个出栈的数为k”的方案数，k从1取至n，则有

$$f(n)=\sum _{i=1}^{n}f(i-1)\ast f(n-i)=\sum _{i=0}^{n-1}f(i)\ast f(n-i-1)$$

同样符合卡特兰数的情形。

那么进一步思考一下，为什么两个看似无关的问题，最终的解是一样的呢？为了揭示其本质意义，我们换一种角度来看待以上两个问题。

考虑堆栈入栈和出栈方案时，实际上可以认为是n次入栈与n次出栈所组成的组合。那么，令入栈为“1”，出栈为“0”，任何一种方案，都可以等价刻画为一串长度为2n的“01”串，如下图，出栈顺序为1、3、4、2，则对应的“01”串为10110100。

从图中可以看到，01串中的每一位对应了每个时刻，堆栈内发生的操作（入或出）。该串具有以下两个性质：

1. 由n个“1”和n个“0”组成，长度为2n。
2. 取出串的任意前k位，“1”的个数>="0"的个数（否则意味着某时刻对空栈做了pop操作，无实际意义）

01串表现的是对堆栈的操作方法，而所有满足以上两个条件的01串，可以证明与出栈的方案是一一对应的。（任何一种出栈方案都可以找到一种操作方法，且不同的操作方法所产生的出栈顺序总是不同的）因此，“01”串的方案数就是堆栈问题方案数的等价刻画。

同样，我们找一种方法来刻画正多边形连边方案数的问题。选择一个点作为起始点，从起始点出发，逆时针绕多边形一周，对于某一个结点，如果之前访问过与它相连的另一个结点，则记为“0”，如果是第一次访问这条边，则记为“1”。

如图中这种连法对应的“01”串就是“10110010”，该串同样也具有以上两个性质，并且这种刻画方法与原问题的方案也一一对应。

于是总结一下，卡特兰数f(n)的一个本质含义，就是满足

1. 由n个“1”和n个“0”组成，长度为2n。

2. 取出串的任意前k位，“1”的个数>="0"的个数

这两个条件的01串的个数。

为啥要绕这么一大圈呢，一方面是加深一下对卡特兰数的理解，另一方面是因为，单纯从递推的角度，计算f(n)的时间复杂度是O(n^2)，把问题转换成这样，才便于我们找到卡特兰数通项公式。

$$f(n)=\sum _{i=0}^{n-1}f(i)\ast f(n-i-1)=C_{2n}^n-C_{2n}^{n+1}$$

下面来看一下这个公式的神仙推导方法

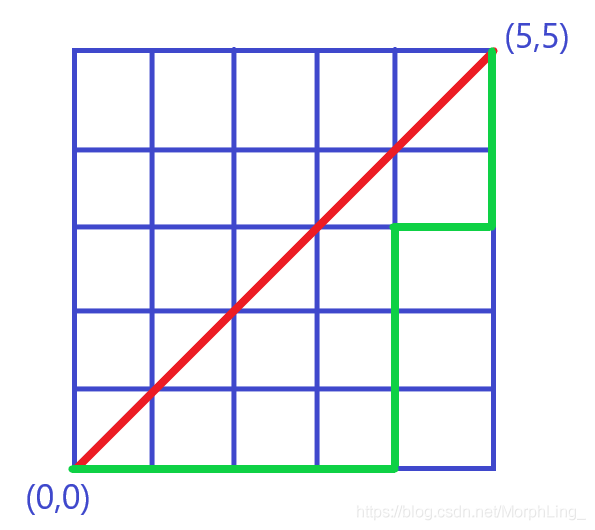
我们再给这样的“01”串赋予一个比较熟悉的实际意义，即从（0，0）沿着网格线，每一步向上或向右走到（n，n）的一种方案。我们令“1”是向右走一步，“0”是向上走一步，那么由性质可知，所有合法的路线都不能穿过红色对角线。只有红线以下（如绿色的线）才是合法的

这里的计算方法是先计算出总共的方案数$C_{2n}^n$，再减去不合法（即越过红线的）方案数。

问题转换后，就有了下图这样一个构造方法：

观察上图不合法的紫线，找到它第一处越过红线的位置，将从这一点起到(5,5)的路径沿着y=x+1这条粉线对称翻转一下，得到了黄线。由对称翻转可知，终点一定被翻转到了(n-1,n+1)也就是(4,6)这一点上。

再把黄线和下半段紫线拼起来，发现这就是一条从(0,0)到(4,6)的路线（即图中绿线）。

由此我们再反过来想，对于每一条从(0,0)到(4,6)的路线，必然会在某一点越过红线，将这一点到(4,6)的部分对称翻转并和前半段拼接，不就得到了一种从(0,0)到(5,5)，且越过红线的方案了嘛。（此处还是有一个经过对称翻转后，两种路线一一对应的关系存在，避免太啰嗦就不展开说了，应该挺好理解的）

总之，通过这样一种构造，可以得到非法方案就是$C_{2n}^{n+1}$（$C_{2n}^{n+1}$=$C_{2n}^{n-1}$）种。用总方案减去非法的，就是合法方案的个数了，如果把组合数再展开一下，就能得到最后的阶乘公式了。
$$f(n)=\sum _{i=0}^{n-1}f(i)\ast f(n-i-1)=C_{2n}^n-C_{2n}^{n+1}=\frac{(2n)!}{n!(n+1)!}$$
（题外话：卡特兰数前几项是：1、2、5、42、132、429、1430、4862…，所以有时手推前几项，可以反过来发现是用卡特兰数来做的）

把卡特兰数讲清楚之后这道题就很显然了。合法方案数就是f(n)，直接代入公式计算。

总方案数是从2n个结点中两两选一组连边，再除以n!消除先后顺序
$$\frac{C_{2n}^2\cdot C_{2n-2}^2\cdot ...\cdot C_2^2}{n!}=\frac{(2n)!}{2^n\cdot n!}$$

合法方案/总方案后得到答案，O (n)计算即可。
$$ans=\frac{2^n}{(n+1)!}$$

#include
using namespace std;
const int MOD=1e9+7;
typedef long long ll;
ll qpower(int x,int p)
{
    ll base=x,ret=1;
    while(p){
        if (p&1==1) ret=(ret*base)%MOD;
        base=(base*base)%MOD;
        p=p>>1;
    }
    return ret;
}
int main(){
    int n;
    ll ans=1,div=1;
    cin>>n;
    for (int i=1;i<=n;i++) ans=(ans*2)%MOD;
    for (int i=1;i<=n+1;i++) div=(div*i)%MOD;
    ans=(ans*qpower(div,MOD-2))%MOD;
    printf("%lld",ans);
    return 0;
}