22降维算法-PCA主成分分析
唐宇迪《python数据分析与机器学习实战》学习笔记
22降维算法-PCA主成分分析
一、算法讲解
比如（3,2）是建立在我的基上，一旦改变就不能这么表达那个点了。
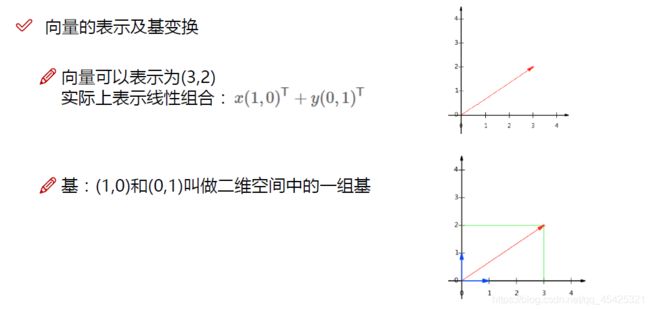
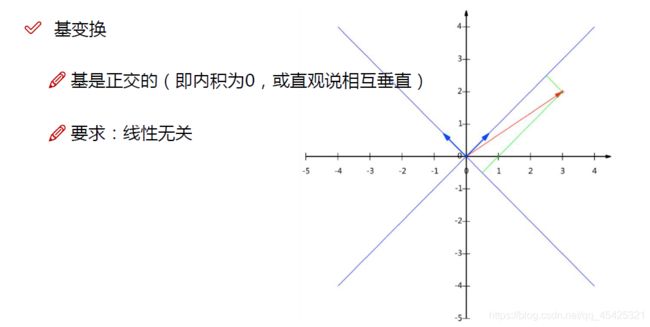
线性无关，X轴Y轴的数据不相互影响。
做事要有依据，既然映射到基，那就要 找最合适的基
一堆密集的点希望投影后得到一堆比较分散的点，因此方差越大越好，方差代表一个特征的分散程度，协方差代表两个变量之间的关系，如果A、B的变化趋势类似则协方差越大，协方差的值在-1到1之间。
协方差计算：第一列减去第一列均值，第二列减去第二列均值，本来应该是（ai-μa）（bi-μb）这里假设均值为0所以直接aibi
之所以要引入协方差是因为：比如10维-2维选方差最大的当轴，第一个轴方差最大，第二个轴次大，两个轴肯定接近重合，即使多个轴也会大部分接近重合，不利于建模。
优化目标
使方差尽可能大、使协方差为0。对角线上是各自的方差（默认μ为0），非对角线上就是两个字段的协方差
让对角线上有值，而非对角线的位置是协方差因此让其所有为0。
数据以0为中心化，再用1/m乘数据乘数据转置得到协方差矩阵，对角线为方差、非对角线为协方差。随后对协方差矩阵进行矩阵分解得到特征值和特征向量。现在想2维变1维，所以取最大的为2那个，然后将1的基单位化（归一化）。降维=基数据。
二、PCA实例
2.1数据获取及展示
数据的读取及查看，150个，4个维度
import numpy as np
import pandas as pd
df = pd.read_csv('iris.data')
df.head()
赋予数据列名
df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
df.head()
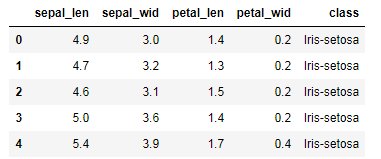
获得XY数据，x是一个150 x4 的矩阵，每一行都是一个样本，y是一个 150 x1 是向量，每个都是一个分类。
X = df.ix[:,0:4].values
y = df.ix[:,4].values
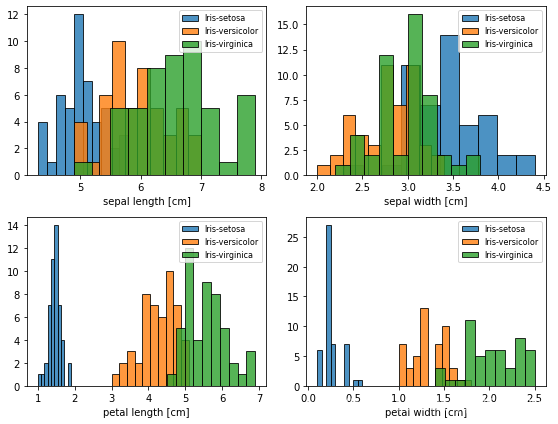
看一下3个类型花（Y）的在每个特征（X）上的分布情况
from matplotlib import pyplot as plt
import math
#Y
label_dict = {1: 'Iris-Setosa', #3个类型的花
2: 'Iris-Versicolor',
3: 'Iris-Virgnica'}
#X
feature_dict = {0: 'sepal length [cm]', #花萼长宽
1: 'sepal width [cm]',
2: 'petal length [cm]', #花瓣长宽
3: 'petal width [cm]'}
plt.figure(figsize=(8, 6)) #图形大小
for cnt in range(4):
plt.subplot(2, 2, cnt+1) #绘图位置
for lab in ('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'): #3个类别遍历绘图
plt.hist(X[y==lab, cnt], #柱形图绘制，依次传入xy
label=lab,
bins=10,
alpha=0.8,
edgecolor='black',)
plt.xlabel(feature_dict[cnt]) #标题名
plt.legend(loc='upper right', fancybox=True, fontsize=8)
plt.tight_layout() #会自动调整子图参数,使之填充整个图像区域
plt.show()
2.2数据标准化
我们将数据转化为 mean=0 and variance=1 的数据
from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)
print (X_std)
2.3特征分解—主成分选择—投影矩阵构造—投影
第一步X乘以XT乘以(1/m)，这里用的1/(m-1) ，得到协方差矩阵
mean_vec = np.mean(X_std, axis=0) #均值为0，X_std.std(axis=0) 则方差为1
cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
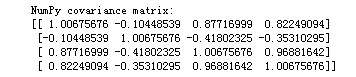
print('Covariance matrix \n%s' %cov_mat)
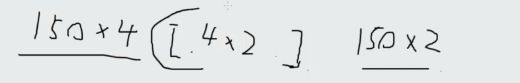
150x4的想变成150x2的需要乘以一个4x2矩阵，接下来求这个4x2的投影矩阵
print('NumPy covariance matrix: \n%s' %np.cov(X_std.T))#上面操作的简化
由特征矩阵分解为：特征值和特征向量
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)#获取特征值和特征向量
print('Eigenvectors \n%s' %eig_vecs)#特征向量
print('\nEigenvalues \n%s' %eig_vals)#特征值
4个特征向量对应4个特征值，需要选出来两个，特征值衡量其重要程度
下面把特征值和特征向量一一对应起来：
# (特征值，特征向量列)元组
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
print (eig_pairs)
print ('----------')
# 依据特征值排序
eig_pairs.sort(key=lambda x: x[0], reverse=True)
# 看看是不是真的递减排序了
print('Eigenvalues in descending order:')
for i in eig_pairs:
print(i[0])
特征重要性可视化操作
tot = sum(eig_vals)
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)] #转为特征所占的百分比
print (var_exp)
cum_var_exp = np.cumsum(var_exp) #[1,2,3,4]cumsum后为[1,3,6,10] 依次叠加前面的
cum_var_exp
可视化：
plt.figure(figsize=(6, 4))
plt.bar(range(4), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(4), cum_var_exp, where='mid',
label='cumulative explained variance')
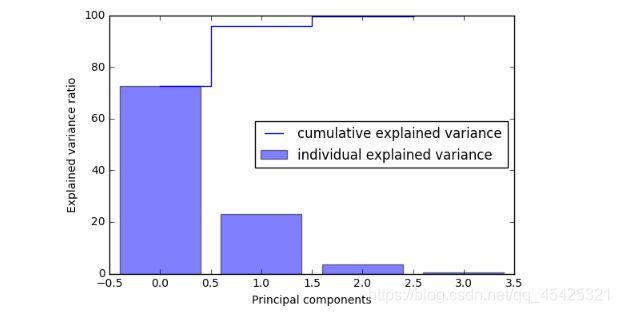
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
然后把排名前2的两个拿出来组合为4x2的
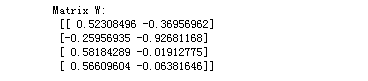
matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1),
eig_pairs[1][1].reshape(4,1))) #将[1,4]结构转为[4,1]再组合起来
print('Matrix W:\n', matrix_w)
接下来变换维度，变为150x2的了
Y = X_std.dot(matrix_w)
Y
2.4效果展示
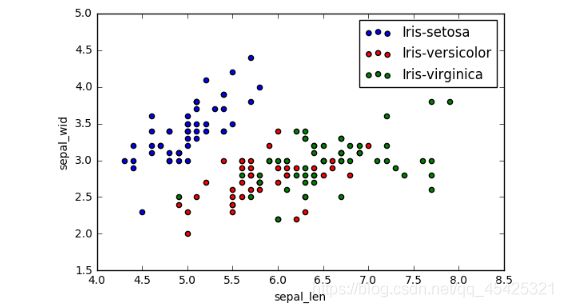
变换前
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(X[y==lab, 0],
X[y==lab, 1],
label=lab,
c=col)
plt.xlabel('sepal_len')
plt.ylabel('sepal_wid')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
变换后
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(Y[y==lab, 0],
Y[y==lab, 1],
label=lab,
c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()
总结：分辨能力更强了