2020牛客暑假多校第二场补题
比赛链接:link
题目
- A kmp + Hash
- B 几何
- C dfs
- D 签到题
- F 单调区间 + gcd筛
- G bitset神奇用法
- H 权值线段树(动态开点/离散化)
- J 群论
A kmp + Hash
题意是说,定义了两个字符串间的函数 f ( s , t ) f(s, t) f(s,t) 表示字符串 s s s 的前缀和字符串 t t t 后缀能相等的最大长度,而总共有 n n n 个串,求 ∑ i = 1 n ∑ j = 1 n f ( s i , s j ) \sum_{i = 1}^{n} \sum_{j=1}^{n} f(s_i, s_j) ∑i=1n∑j=1nf(si,sj)。其中 1 ≤ n ≤ 1 e 5 1 ≤ n ≤ 1e5 1≤n≤1e5, ∑ ∣ s i ∣ ≤ 1 e 6 \sum|s_i| ≤ 1e6 ∑∣si∣≤1e6。
比赛中这题过的人不是很多,感觉也没有很巧的解法。暴力的话,我们可以先将每个字符串的后缀处理出来,由于 ∑ ∣ s i ∣ ≤ 1 e 6 \sum|s_i| ≤ 1e6 ∑∣si∣≤1e6,那么最多有 1 e 6 1e6 1e6 个后缀,然后再遍历前缀来和存下来的后缀匹配。但是这样的话一定是会重复的,比如只有一个串 a b a aba aba,我存的后缀有 a a a, b a ba ba, a b a aba aba, 那么我遍历前缀的时候 a a a 和 a b a aba aba 都可以匹配到,但是我们只需要长度最大的那个,这该如何去重呢?
我们可以再举一个例子来看一看,比如 a b a b a ababa ababa 与自身匹配,进行遍历前缀时:
① a a a 匹配到,所以 a n s [ 1 ] + + ans[1]++ ans[1]++(记录个数);
② a b ab ab匹配不到;
③ a b a aba aba 匹配得到,所以我们现在知道 a a a 会重复,所以 a n s [ 1 ] − − , a n s [ 3 ] + + ans[1]--, ans[3]++ ans[1]−−,ans[3]++;
④ a b a b abab abab 匹配不到;
⑤ a b a b a ababa ababa 匹配到,所以我们现在知道 a b a aba aba 重复,所以 a n s [ 3 ] − − , a n s [ 5 ] + + ans[3]--, ans[5]++ ans[3]−−,ans[5]++。
所以我们每匹配到一个前缀,就要减去其能相等的最大长度的前后缀的计数(不包括自身),而这正好就是 kmp 算法里的 next 数组(或者叫 fail 失败链接)。
而存后缀的话,翻了翻 AC 代码,大部分人都是通过函数 ∑ i = 0 l e n − 1 s [ i ] ∗ 13 1 i \sum_{i = 0}^{len-1} s[i] * 131^i ∑i=0len−1s[i]∗131i 将字符串转为 unsigned long long, 然后用 map 进行映射,所以我也采取了这种哈希方式,这样的映射稍微长一点的字符串肯定会自然溢出,但是相等的字符串一定能映射成相同的数值。
需要注意的是,用普通的 map 花了 2.4 s 2.4s 2.4s, 而用 unordered_map 花了 0.9 s 0.9s 0.9s,所以如果卡 map 的常数,一定要用
unordered_map。
#include 然后还有很多大佬用了自己写的 Hash_map…还有 AC 自动机的做法, 待补。
B 几何
题目大意是给了 n ( n ≤ 2000 ) n \ (n ≤ 2000) n (n≤2000) 个二维坐标点,问最多多少个点可以共圆 (这个圆必须经过原点)。
看这个数据量,应该是平方的,可以枚举。由于三点不共线确定一个圆,而圆必过原点,只要枚举剩下两个顶点就好了。当确定了原点和点 i i i 之后,如果原点,点 i i i,点 j 1 j_1 j1 确定的圆心与原点,点 i i i,点 j 2 j_2 j2 确定的圆心相等,那么 i i i, j 1 j_1 j1, j 2 j_2 j2 就可以共圆。
所以我们需要记录圆心,通过数学推导, ( 0 , 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) (0, 0), (x_1, y_1), (x_2, y_2) (0,0),(x1,y1),(x2,y2) 若是不共线,即 k = x 1 y 2 − x 2 y 1 ≠ 0 k = x_1 y_2 - x_2 y_1 ≠ 0 k=x1y2−x2y1=0:
X = y 2 ( x 1 2 + y 1 2 ) − y 1 ( x 2 2 + y 2 2 ) 2 k X = \frac{y_2 (x_1^2 + y_1^2) - y_1 (x_2^2 + y_2^2)}{2k} X=2ky2(x12+y12)−y1(x22+y22) Y = x 1 ( x 2 2 + y 2 2 ) − x 2 ( x 1 2 + y 1 2 ) 2 k Y = \frac{x_1 (x_2^2 + y_2^2) - x_2 (x_1^2 + y_1^2)}{2k} Y=2kx1(x22+y22)−x2(x12+y12)
这个算出来是浮点数,我比赛的时候觉得用 map 去存肯定有精度误差,所以就不敢(但是居然这样可以过…),我是记录完再排序,若是两个相邻点的误差在 eps 范围内,就认为相等。其实更精确的方法是用分数形来记录,但是这样会超时…
由于遍历记录完还要排序,那么总复杂度为 O ( n l o g n ) O(nlogn) O(nlogn), wa 了好多发的原因是没有开 long long,哎…
#include
C dfs
题目是说给定一棵树,求最少的链,保证每个点都至少被一条链覆盖。
由于树可能很大,那么树的形状那么多,所以觉得可能和具体的树的形状无关。考虑到叶子结点必须被覆盖,且叶子结点至少占了一条链的一端,那么至少需要 c e i l ( n u m ( l e a f ) 2 ) ceil(\frac{num(leaf)}{2}) ceil(2num(leaf)) 条链。试了很多树,发现这么多链是可以覆盖所有树的。
但是并非任意的叶子结点相连形成链都可以,比如下图:
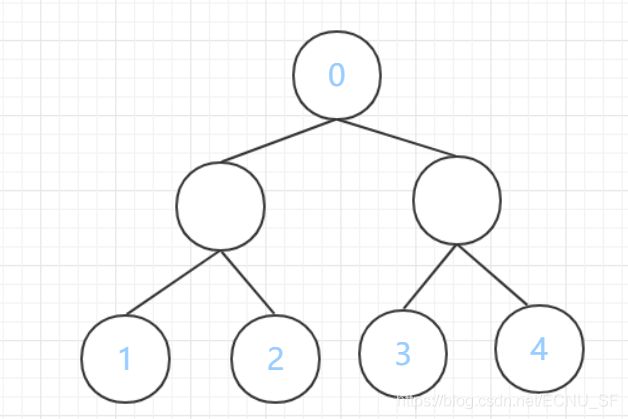
如果链 1-2, 3-4 的话,结点 0 就不会覆盖到,必须要 1 与 3 连接, 2 与 4 连接,所以我们可以 dfs 记录所有的叶子结点,然后让前半部分的叶子结点与后半部分的叶子结点相连,如 1 与 3, 2 与 4。
#include
D 签到题
只需要把时间换成秒一剪就好啦,用 scanf 读就很舒服,可以处理掉 :。
#include
F 单调区间 + gcd筛
题意是说给定一个 n × m n×m n×m 的矩阵 A A A,其中 A i j = l c m ( i , j ) A_{ij} = lcm(i, j) Aij=lcm(i,j),对于大矩阵每一个 k × k k × k k×k 的子矩阵,都有一个最大值,我们求这些最大值的和。
感觉矩阵里的每个元素还是要算出来的, 要是直接算的话,复杂度为 O ( n m l o g n ) O(nmlogn) O(nmlogn), 可以用对称相等来稍微优化一下。标程给了一种筛法,可以去掉那个log, 感觉有点像埃筛:
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
if (!A[i][j])
for (int k = 1; k * i <= n && k * j <= m; k ++)
A[k * i][k * j] = k;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
A[i][j] = i * j / A[i][j];
带个 log 也能过,接下来就是找最大值了。对于一维区间,遍历长度为 k k k 的最大值 可以用经典的单调队列来做,而这个二维矩阵我们只需要对两维都来一遍就好了,这里对单调队列有一个比较详细的说明,就不赘述(link)
#include
G bitset神奇用法
题目大意是给定长度为 n n n 的序列 A 和长度为 m m m 的序列 B,其中 n ≥ m n ≥ m n≥m, A中可以截取长度为 m m m 的连续区间 S S S, 问满足对于任意 1 ≤ i ≤ m 1 ≤i ≤ m 1≤i≤m, 都有 S i ≥ B i S_i ≥ B_i Si≥Bi 的区间个数。其中 m ≤ 4 e 4 , n ≤ 1.5 e 5 m ≤ 4e4,n ≤ 1.5e5 m≤4e4,n≤1.5e5。
看了好久才看懂标程…首先为了之后的状态转移,对于每一个 A i A_i Ai,都有一个 bitset I [ i ] I[i] I[i],若 I [ i ] [ j ] = 1 I[i][j] = 1 I[i][j]=1, 表示 A i ≥ B j A_i ≥ B_j Ai≥Bj, 反之为 0 表示 A i < B j A_i < B_j Ai<Bj。若是单纯的暴力匹配得 bitset 的值,我们的空间复杂度和时间复杂度都是 O ( n m 64 ) O(\frac{nm}{64}) O(64nm), 所以我们可以考虑先排序,用双指针的方式进行遍历。因为若 A i 1 ≤ A i 2 A_{i_1} ≤ A_{i_2} Ai1≤Ai2,那么 I [ i 1 ] I[i_1] I[i1] 为 1 的地方, I [ i 2 ] I[i_2] I[i2] 也一定为1, 所以排序之后,后一个数的 bitset 可以在前一个数 bitset 的基础上进行修改。
而其实我们也不需要 n n n 个 bitset, 因为序列 B 长度为 m m m, 所以最多有 m + 1 m + 1 m+1 个不同的 bitset, 这样空间复杂度可以降到 O ( m 2 64 ) O(\frac{m^2}{64}) O(64m2)。
接下来比较重要的就是这个转移方法了,我们用一个长度为 m + 1 m + 1 m+1 的 bitset,来记录状态,若第 i i i 位为 1,表示当前可以匹配到 序列B 的前 i i i 位,否则表示没有匹配到。这个还是需要例子来说明,若 A = [ 1 , 2 , 2 , 3 , 5 ] , B = [ 1 , 2 , 3 ] A = [1, 2, 2, 3, 5], B = [1, 2, 3] A=[1,2,2,3,5],B=[1,2,3], bitset 初始为 [ 1 , 0 , 0 , 0 ] [1, 0, 0, 0] [1,0,0,0](第 0 位为 1 表示可以匹配到的区间长度为0)
①当前匹配到区间长度为0,我们尝试去扩展区间,由于 A [ 1 ] ≥ B [ 1 ] A[1] ≥ B[1] A[1]≥B[1],bitset 变成 [ 1 , 1 , 0 , 0 ] [1, 1, 0, 0] [1,1,0,0];
②当前匹配到区间长度为0或1,我们尝试去扩展区间,由于 A [ 2 ] ≥ B [ 1 ] , A [ 2 ] ≥ B [ 2 ] A[2] ≥ B[1],A[2] ≥ B[2] A[2]≥B[1],A[2]≥B[2], bitset 变成 [ 1 , 1 , 1 , 0 ] [1, 1, 1, 0] [1,1,1,0]
③当前匹配到区间长度为0或1或2,我们尝试去扩展区间,由于 A [ 3 ] ≥ B [ 1 ] , A [ 3 ] ≥ B [ 2 ] A[3] ≥ B[1],A[3] ≥ B[2] A[3]≥B[1],A[3]≥B[2],但 A [ 3 ] < B [ 3 ] A[3] < B[3] A[3]<B[3], bitset 变成 [ 1 , 1 , 1 , 0 ] [1, 1, 1, 0] [1,1,1,0]
④当前匹配到区间长度为0或1或2,我们尝试去扩展区间,由于 A [ 4 ] ≥ B [ 1 ] , A [ 4 ] ≥ B [ 2 ] , A [ 4 ] ≥ B [ 3 ] A[4] ≥ B[1],A[4] ≥ B[2],A[4] ≥ B[3] A[4]≥B[1],A[4]≥B[2],A[4]≥B[3],bitset 变成 [ 1 , 1 , 1 , 1 ] [1, 1, 1, 1] [1,1,1,1], 答案+1;
④当前匹配到区间长度为0或1或2,我们尝试去扩展区间,由于 A [ 5 ] ≥ B [ 1 ] , A [ 5 ] ≥ B [ 2 ] , A [ 5 ] ≥ B [ 3 ] A[5] ≥ B[1],A[5] ≥ B[2],A[5] ≥ B[3] A[5]≥B[1],A[5]≥B[2],A[5]≥B[3],bitset 变成 [ 1 , 1 , 1 , 1 ] [1, 1, 1, 1] [1,1,1,1], 答案+1;
扩展区间操作相当于将当前 bitset 向左移一位,然后与 I [ i ] I[i] I[i] 进行与操作: c u r = ( c u r < < 1 ) & I [ i ] cur = (cur<<1) \& I[i] cur=(cur<<1)&I[i]
#include 然后翻别的大佬的 AC 代码,看到一个只用两个 bitset 就过了的…太神仙了,理解了好久,不太能写出来…大致思路是设置一个长度为 n n n 的 bitset, 一开始全部初始化为 1,第 i i i 位为1表示从当前开始长度为 m m m 的区间满足要求,然后通过从大到小遍历来去掉不可能的位置。这内存压的太nb了。
#include
H 权值线段树(动态开点/离散化)
大致题意是说给定一个允许有重复整数元素的集合,第一种操作是增加一个整数,第二种操作是删除一个整数,第三种操作是给定一个整数,判断是否能从集合内再找两个整数组成一个三角形。
第一种操作和第二种操作直接用 STL 的 multiset 就可以做到,但是第三种操作就不好维护了。
若是判断的整数 x x x是三角形的最大边,那么只需要在小于等于 x x x 的集合元素中挑选两个最大的相加判断是否大于 x x x;若是判断的整数是中间边,只需要挑选小于等于 x x x 的最大元素和大于等于 x x x 的最小元素就可以;若是最小边的话,在大于等于 x x x 的元素里挑选,一定是挑选两条差值最小的边。所以最关键的还是动态的记录相邻边的差值。
赛后看了别人的解法,也是类似的,第一种第二种操作用 map 来记录个数即可,若记第三种操作挑选的元素是 a , b ( b ≥ a ) a, b \ (b ≥ a) a,b (b≥a),那么能组成三角形等价于 b − a < x < b + a b - a < x < b + a b−a<x<b+a,若是我们记 b b b 的前驱结点为 b ′ b' b′ (小于等于 b b b 的最大整数,可以相等),那么我们有 b − b ′ ≤ b − a < x < b + a ≤ b + b ′ b - b' ≤ b - a < x < b + a ≤ b + b' b−b′≤b−a<x<b+a≤b+b′,那么若存在 a a a 可以, b ′ b' b′ 一定可以。
我们记 k = l o w e r _ b o u n d ( x / 2 + 1 ) k = lower \_ bound(x / 2 + 1) k=lower_bound(x/2+1),那么 b m i n ≥ k b_{min} ≥ k bmin≥k, 若是 k + k ′ ≤ x k + k' ≤ x k+k′≤x,那么 b m i n = k . n e x t b_{min} = k.next bmin=k.next,否则 b m i n = k b_{min} = k bmin=k (这里可以仔细想一想),而我们只需要判断在 大于等于 b m i n b_{min} bmin 的元素中,有没有和前驱元素差值小于 x x x 的,这个就由权值线段树来维护。
由于区间可以到 1 e 9 1e9 1e9,所以采取了动态开点的方式(也是第一次学了这种操作),大部分与普通线段树差不多,理解理解代码就好啦。若是添加一个元素集合里没有,那么对后面,自身元素有影响,若是集合里只有一个,那么对自身有影响;若是删除一个元素后集合里只有一个,那么对自身有影响,若是集合里就没有了,那么对自身和后面元素有影响。
#include 除了动态开点还有离散化的做法,待补。
J 群论
题意是说一开始给你一个排列 { 1 , 2 , 3... n } \{1, 2, 3...n\} {1,2,3...n},经过 k k k 次置换,变成 { a 1 , a 2 . . . . a n } \{a_1, a_2....a_n\} {a1,a2....an},问若是将原来的排列只置换一次,会变成什么?( 1 ≤ n ≤ 1 e 5 1 ≤ n ≤ 1e5 1≤n≤1e5, k k k 为质数)
首先什么是排列的置换呢?根据抽象代数里的定义,一个集合的排列置换是自身对自身的一个双射。 这可以理解成将一个排列的元素打乱顺序,得到一个新的排列。比如排列 { 1 , 2 , 3 , 4 , 5 } \{1, 2, 3, 4, 5\} {1,2,3,4,5} 可以经过 k k k 次置换变成了 { 5 , 3 , 4 , 1 , 2 } \{5, 3,4,1,2\} {5,3,4,1,2}。
而排列是可以分解成若干 cycle 的。比如上面的排列,原来的第 1 位 变成了原来的第 5 位, 第 5 位变成了原来的第 2 位,第 2 位变成了原来的第 3 位,第 3 位变成了原来的第 4 位,第 4 位变成了原来的第 1 位,这样就可以写作一个 cycle : ( 1 , 5 , 2 , 3 , 4 ) (1, 5, 2, 3, 4) (1,5,2,3,4)。再比如 k k k 次置换变成了 { 5 , 3 , 4 , 2 , 1 } \{5, 3,4,2,1\} {5,3,4,2,1}, 可以写作 2 个 cycle: ( 1 , 5 ) ( 2 , 3 , 4 ) (1,5)(2,3,4) (1,5)(2,3,4)。
我们可以发现,若经过 k k k 次置换变成了 { 5 , 3 , 4 , 1 , 2 } \{5, 3,4,1,2\} {5,3,4,1,2},那么经过 5 k 5k 5k 次置换可以变回 { 1 , 2 , 3 , 4 , 5 } \{1,2,3,4,5\} {1,2,3,4,5}。其实 k k k 次置换可以看成一个双射函数,而 t k tk tk 次置换就是一个复合函数,接下来就推一推。
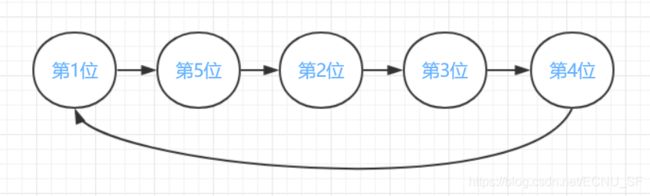
k k k次变换对应的 cycle 即为上图,以第 1 1 1 位为例,一开始是 1 1 1:
①经过 k k k 次变换后变成了原来的第 5 5 5 位,所以 k k k 次变换后为 5 5 5;
②经过 2 k 2k 2k 次变换后变成了 k k k次变换后的 第 5 5 5 位,即没有变换时的第 2 2 2 位,所以 2 k 2k 2k 次变换后为 2 2 2;
③经过 3 k 3k 3k 次变换后变成了 2 k 2k 2k次变换后的 第 5 5 5 位,即 k k k次变换后的 第 2 2 2 位,没有变换时的第 3 3 3 位,所以 3 k 3k 3k 次变换后为 3 3 3;
④经过 4 k 4k 4k 次变换后变成了 3 k 3k 3k次变换后的 第 5 5 5 位,即 2 k 2k 2k次变换后的 第 2 2 2 位, k k k次变换后的 第 3 3 3 位,没有变换时的第 4 4 4 位,所以 4 k 4k 4k 次变换后为 4 4 4;
⑤经过 5 k 5k 5k 次变换后又回到了 1 1 1。
若记上述的 cycle 的变换关系为 b [ ] = { 1 , 5 , 2 , 3 , 4 } b[] = \{1, 5, 2, 3, 4\} b[]={1,5,2,3,4},那么 经过 t k tk tk 次变换后 a [ 1 ] = b [ ( t + 1 ) % 5 ] a[1] = b[(t +1)\% \ 5] a[1]=b[(t+1)% 5],推广一下可以得到 经过 t k tk tk 次变换后: a [ i ] = b [ ( t + i ) % l e n ( c y c l e ) ] a[i] = b[(t + i)\% \ len(cycle)] a[i]=b[(t+i)% len(cycle)]。
我们在这里可以知道,一个 cycle 的元素要返回原来的位置,要经过 l e n ( c y c l e ) ∗ k len(cycle) * k len(cycle)∗k 次变换;若得到所有 cycle 的 lcm, 那么整个排列要返回自身就是 l c m ∗ k lcm * k lcm∗k 次变换。
当我们知道了一个 cycle t k tk tk 次变化后对应到什么,那么对于一个排列可以分解为若干 cycle, 分开处理即可。我们最终要求的是置换 1 1 1 次的结果,即对于每一个 cycle,长度为 l i l_i li, 都进行 t i k t_ik tik 次变换,其中 t i k ≡ 1 ( m o d l i ) t_ik ≡ 1 \ (mod \ l_i) tik≡1 (mod li), 即 k k k 对于 l i l_i li 的逆元,若是有一个同余方程无解,则说明解不存在,但是由于 k k k 为质数,所以 t i t_i ti 肯定有解,可以通过枚举或者扩展欧几里得的方法得到 t i t_i ti。
由于对于每一个 cycle 都可以线性时间得到逆元和进行置换,所以总复杂度为 O ( n ) O(n) O(n)
#include