交叉熵/二分类交叉熵及各自对应的focal loss(附pytorch代码)
对于二分类问题,使用softmax或者sigmoid,在实验结果上到底有没有区别(知乎上相关问题讨论还不少)。最近做的相关项目也用到了这一块,从结果上来说应该是没什么区别,但是在模型上还是存在一定差异性的(可以应用于多模型融合、在相关比赛项目当中还是可以使用的)。相关知识和代码总结如下。
以下主要分为4个部分:交叉熵损失、二分类交叉熵损失、Focal loss及二分类Focal loss
1. CE_loss
import torch.nn.functional as F

F.cross_entropy是log_softmax和nll_loss的组合,log_softmax就是log和softmax的组合,nll_loss为:

注意,这里面包括了将output进行Softmax操作的,所以直接输入output即可。其中还包括将label转成one-hot编码,所以直接输入label。该函数限制了target的类型为torch.LongTensor。label_tgt = make_variable(torch.ones(feat_tgt.size(0)).long())可在后边直接.long()。其output,label的shape可以不一致。

里面有一个weight参数,默认为0,是为解决类别样本不平衡问题的,对于含有样本非常多的某一类别,可以使其在loss中weight更低一些。
1.1 任务为二分类时,y为标签(0/1),p为模型预测概率
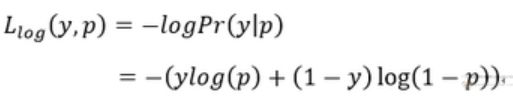
1.2 任务为多元分类时,样本标签为one-hot向量,则N个样本,在K个类别情况下,其总体损失如下;
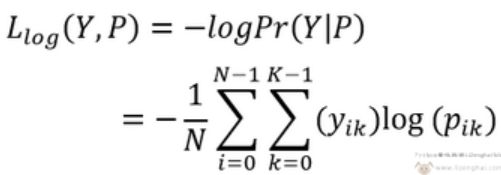
1.3 任务为多标签分类时,比如一张图象同时含有猫和狗等,与之前不一样的是,预测不再通过softmax计算,而是采用sigmoid把输出限制到(0,1)。正因此预测值得加和不再是1。这里交叉熵单独对每一个类别计算,每一个类别有两种可能的类别,即属于这个类的概率或不属于这个类的概率。

2. BCE_loss

注意这里的二分类损失,跟上面的二分类损失计算有一些区别,上面默认的使用了softmax函数,其一个样本对应2个类别的概率,且加和为1。 而这里的logit的对应输出可以是一维的sigmoid输出,值以0.5为界分为2个类别。
注意input,target的shape必须相等,且input应该为FloatTensor的类型。
3. CE_focal_loss
Focal loss是在交叉熵损失函数上进行的修改,主要是为了解决正负样本严重失衡的问题,降低了简单样本的权重,是一种困难样本的挖掘。
二分类交叉熵、交叉熵损失及对应focal loss分别如下:
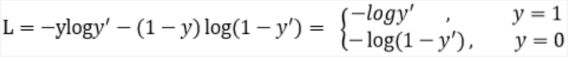
![]()
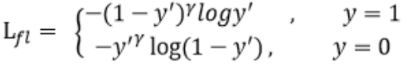
![]()
可以看到损失前面增加了一个系数,且系数有个次幂。
以二分类focal loss=L_fl为例,y’表示模型预测结果,当标签y=1时,预测结果y’越接近于1则整体损失系数值越小,表示为简单样本;反之当y=1,而预测y’越接近于0,则其损失系数值越大。

注意这里的alpha设置,还是需要考虑清楚一些的,对于样本数量少的类别(如文中提到的正样本比负样本少),反而其权重要设置的小一些,为什么呢:因为系数的设置,样本少的类别可以理解为困难样本,对于困难样本focal loss本身设置的系数比较大,所以对应的alpha要设置小一些。
class FocalLoss(nn.Module):
def __init__(self, num_class=2, alpha=0.6, gamma=2, balance_index=0, smooth=None, size_average=True):
super(FocalLoss, self).__init__()
self.num_class = num_class
self.alpha = alpha
self.gamma = gamma
self.smooth = smooth
self.size_average = size_average
if self.alpha is None:
self.alpha = torch.ones(self.num_class, 1)
elif isinstance(self.alpha, (list, np.ndarray)):
assert len(self.alpha) == self.num_class
self.alpha = torch.FloatTensor(alpha).view(self.num_class, 1)
self.alpha = self.alpha / self.alpha.sum()
elif isinstance(self.alpha, float):
alpha = torch.ones(self.num_class, 1)
alpha = alpha * (1 - self.alpha)
alpha[balance_index] = self.alpha
self.alpha = alpha
else:
raise TypeError('Not support alpha type')
if self.smooth is not None:
if self.smooth < 0 or self.smooth > 1.0:
raise ValueError('smooth value should be in [0,1]')
def forward(self, input, target):
logit = F.softmax(input, dim=1)
if logit.dim() > 2:
logit = logit.view(logit.size(0), logit.size(1), -1)
logit = logit.permute(0, 2, 1).contiguous()
logit = logit.view(-1, logit.size(-1))
target = target.view(-1, 1)
epsilon = 1e-10
alpha = self.alpha
if alpha.device != input.device:
alpha = alpha.to(input.device)
idx = target.cpu().long()
one_hot_key = torch.FloatTensor(target.size(0), self.num_class).zero_()
one_hot_key = one_hot_key.scatter_(1, idx, 1)
if one_hot_key.device != logit.device:
one_hot_key = one_hot_key.to(logit.device)
if self.smooth:
one_hot_key = torch.clamp(
one_hot_key, self.smooth, 1.0 - self.smooth)
pt = (one_hot_key * logit).sum(1) + epsilon
logpt = pt.log()
gamma = self.gamma
alpha = alpha[idx]
loss = -1 * alpha * torch.pow((1 - pt), gamma) * logpt
if self.size_average:
loss = loss.mean()
else:
loss = loss.sum()
return loss
4. BCE_focal_loss
class BCEFocalLoss(torch.nn.Module):
def __init__(self, gamma=2, alpha=0.6, reduction='elementwise_mean'):
super().__init__()
self.gamma = gamma
self.alpha = alpha
self.reduction = reduction
def forward(self, _input, target):
pt = torch.sigmoid(_input)
#pt = _input
alpha = self.alpha
loss = - alpha * (1 - pt) ** self.gamma * target * torch.log(pt) - \
(1 - alpha) * pt ** self.gamma * (1 - target) * torch.log(1 - pt)
if self.reduction == 'elementwise_mean':
loss = torch.mean(loss)
elif self.reduction == 'sum':
loss = torch.sum(loss)
return loss