本系列是台湾大学资讯工程系林軒田(Hsuan-Tien Lin)教授开设的《机器学习基石》课程的梳理。重在梳理,而非详细的笔记,因此可能会略去一些细节。
该课程共16讲,分为4个部分:
- 机器什么时候能够学习?(When Can Machines Learn?)
- 机器为什么能够学习?(Why Can Machines Learn?)
- 机器怎样学习?(How Can Machines Learn?)
- 机器怎样可以学得更好?(How Can Machines Learn Better?)
本文是第1部分,对应原课程中的1-3讲。虽然第4讲在原课程中也放入了第1部分,但我认为它与后面第2部分的连贯性更强,因此移到后面。
本部分的主要内容:
- 介绍机器学习的概念与流程,并将它和其他几个相似的领域进行比较;
- 介绍感知机模型,说明普通的感知机学习算法PLA在什么条件下可以停下,如果不满足条件该怎么办;
- 列举机器学习的类别。
1 机器学习的概念
1.1 定义
机器学习的定义:improving some performance measure with experience computed from data。
什么时候可以用机器学习?有几个关键的地方:
- 确实存在一些需要学习的“潜在模式”,如预测下一次丢骰子的点数,就不能用机器学习;
- 没有简单的可编程的定义,如判断一张图像中是否包含了圆,就可以直接通过编程解决,不需要使用机器学习;
- 有一些关于要学习的模式的数据,如预测未来核能的滥用是否会导致地球毁灭,就不能用机器学习,因为没有历史数据。
1.2 组成部分
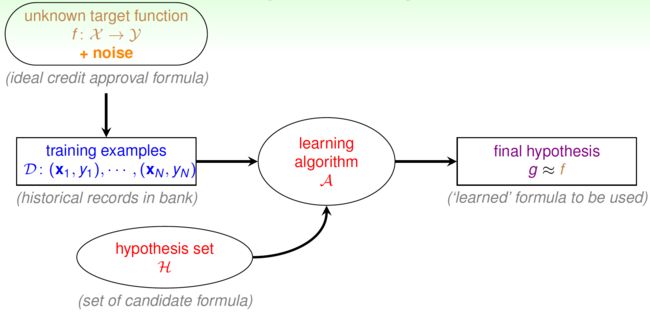
机器学习的实用定义如下图(灰字是以信用卡审批为例):
可以看到,机器学习有以下几个要素:
- 未知的目标函数\(f: \mathcal X\rightarrow\mathcal{Y}\),在例中为理想的信用卡审批规则;
- 训练样本\(\mathcal{D}\),在例中为银行中信用卡审批的历史记录;
- 假设集\(\mathcal{H}\),在例中为一系列的候选规则;
- 学习算法\(\mathcal{A}\);
- 最终挑选出的假设\(g\),满足\(g\approx f\),在例中为最终“学习”出的规则。
机器学习的实用定义:使用数据计算出最接近于目标函数\(f\)的假设\(g\)。
1.3 和其他领域的关系
1.3.1 数据挖掘(DM)
数据挖掘:用(大)数据寻找感兴趣的性质。
- 如果这里所说的“感兴趣的性质”就是“接近目标函数的假设”,那么机器学习就等同于数据挖掘;
- 如果“感兴趣的性质”与“接近目标函数的假设”是相关的,那么数据挖掘可用来帮助机器学习,反之亦然;
- 传统的数据挖掘还关注在大数据库中的有效计算。
在现实中,很难区分ML和DM。
1.3.2 人工智能(AI)
人工智能:计算一些的有智能行为的东西。
如果\(g\approx f\)就是那个有智能行为的东西,那么ML可用于实现AI。
如下棋,传统AI的做法是做博弈树,而ML的做法是从大量数据中进行学习。因此,机器学习是实现人工智能的一种途径。
1.3.3 统计学(Statistics)
统计学:使用数据对未知过程进行推断。
- 如果推断的结果就是\(g\),\(f\)是未知的,那么统计学就可以就用来实现机器学习;
- 传统的统计学聚焦于在数学假设下可证明的结果,而不太关注计算。
统计学为机器学习提供了很多有用的工具。
2 分类学习之感知机模型
2.1 PLA
这里介绍一个简单的分类模型:感知机(Perceptron)。
回顾上一节,在假设集\(\mathcal{H}\)中,我们可以使用哪些假设?
在分类问题中,要预测的变量是正/负,或表示成\(+1\)/\(-1\)。我们可以对自变量做线性加权求和,然后设定一个阈值,若高于阈值,则分类为正,若低于阈值,则分类为负。若将“阈值”也看作在自变量中补入的常数项(\(\mathbb{w}\)中补入对应的常数1),则这个模型可以写作\(h(x)=\text{sign}(\mathbf{w}^T\mathbf{x})\)。
每一个\(\mathbb{w}\),都对应了一个假设。
那么,要如何从假设集\(\mathcal{H}\)中找出最接近于目标函数的\(g\)呢?也就是如何找出最好的\(\mathbb{w}\)?
可以这样做,先任意设一个初始的\(\mathbf{w}_0\)(比如\(\mathbf{0}\)),然后:
- 从该点开始,寻找错误分类的样本点,即找到满足\(\text{sign}(\mathbf{w}^T_t \mathbf{x}_{n(t)})\ne y_{n(t)}\)的点\((\mathbf{x}_{n(t)}, y_{n(t)})\);
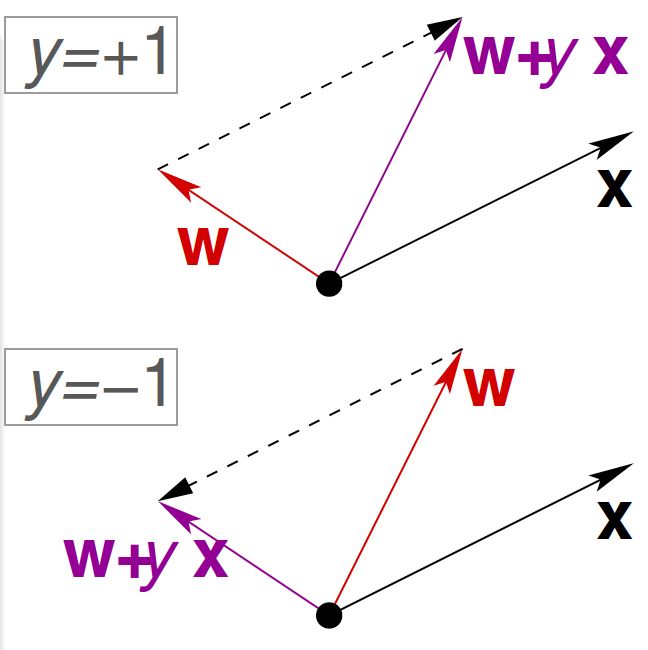
- 利用找到的错误分类点对\(\mathbf{w}\)进行更新,更新规则是:\(\mathbf{w}_{t+1}\leftarrow\mathbf{w}_t +y_{n(t)}\mathbf{x}_{n(t)}\)。
- 不断重复上述过程,直到找不出错误分类的点为止,最终得到要找的\(\mathbf{w}_{PLA}\),把它作为\(g\)。
这就是感知机学习算法PLA(Perceptron Learning Algorithm)。更新规则的图示如下:
但是,以上算法仍然有不少问题:
- 该如何遍历所有的样本点?
- 它最终会停下来吗?需要满足什么条件?
- 停下来说明在样本\(\mathcal{D}\)内已经没有错误了,\(g\approx f\),那么在样本\(\mathcal{D}\)外有用吗?
- 如果不满足使它能停下的条件怎么办?
2.2 PLA会停下吗?
PLA能停下来的必要条件是,存在一些\(\mathbf{w}\)可以在\(\mathcal{D}\)内不会犯错。这叫线性可分(linear separable)条件。那么,线性可分是PLA能停下来的充分条件吗?
答案是肯定的。证明的思路是,既然数据集线性可分,则一定存在某个\(\mathbf{w}\)将样本完美分开,记为\(\mathbf{w}_f\),只需证明在经过有限次的迭代后的\(\mathbf{w}\)和\(\mathbf{w}_f\)的夹角的余弦的下限会超过1即可(因为余弦无法超过1,如果在经过特定次数的迭代后余弦的下限超过了1,说明在上一次迭代之后必定已经完成了完美的分类,无法找出错误分类的点进行迭代了),而余弦可以从分子(两个向量的内积)和分母(两个向量模的乘积)分别突破。具体证明如下:
因为\(\mathbf{w}_f\)能完美分开数据集中的样本,即满足
可令\(\min_\limits{n} y_n \dfrac{\mathbf{w}_f^T}{\Vert \mathbf{w}_f\Vert} \mathbf{x}_n=\rho\),则有
而更新一定是在犯错的点处,所以触发第t次更新的样本一定满足\(y_{n(t-1)}\mathbf{w}^T_{t-1} \mathbf{x}_{n(t-1)}\le 0\)。令\(R^2=\max_\limits{n} \Vert x_n\Vert^2\)(\(R>0\)),则有
接下来就看一看在经过\(T\)次迭代后得到的\(\mathbf{w}_{T}\),它和\(\mathbf{w}_f\)的夹角的余弦:
而余弦必定小于1,因此必有迭代次数\(T\le \dfrac{R^2}{\rho^2}\),证明完毕。
从直觉上理解,PLA算法通过不断迭代,可以使得\(\mathbf{w}\)越来越接近于\(\mathbf{w}_f\)。
PLA算法的优点是简单、快、对任意维度的数据都可用,但缺点在于,一方面我们假设了数据集\(\mathcal{D}\)是线性可分的,而现实中我们不知道是否真的如此,另一方面我们不知道它到底多久会停下,尽管在实践中算法往往很快停下。
2.3 Pocket算法
如果数据中有噪声,导致数据集不是线性可分的,怎么办?
当然,可以直接取\(\mathop{\arg\min}\limits_{w}\sum\limits_{n=1}^{N}{\mathbf{1}_{[y_n\ne \text{sign}(\mathbf{w}^T\mathbf{x}_n)]}}\)作为\(\mathbf{w}_g\),但由于要一一遍历所有样本,这是个NP-hard问题。
那怎么办呢?可以对PLA做一些修改:
- 把当下找到的最佳\(\hat{\mathbf{w}}\)先存起来,就好比放在口袋里;
- 在找到一个使\(\mathbf{w}_t\)分类错误的样本之后,进行和PLA一样的更新,即\(\mathbf{w}_{t+1}\leftarrow\mathbf{w}_t +y_{n(t)}\mathbf{x}_{n(t)}\);
- 比较\(\mathbf{w}_{t+1}\)和\(\hat{\mathbf{w}}\)在整个数据集上谁犯的错误较少,若前者少,则将前者放入口袋,反之仍保留\(\hat{\mathbf{w}}\)在口袋中;
- 不断循环,在经过一定次数的迭代后,停止上述过程,最终在口袋中的\(\hat{\mathbf{w}}\)就取为\(g\)。
由于始终有一个\(\hat{\mathbf{w}}\)在口袋中,因此这种算法被称为Pocket算法。
3. 学习的分类
依据输出空间\(\mathcal{Y}\)的不同来分:
- 二分类问题:\(\mathcal{Y}\)为\(+1\)或\(-1\);
- 多分类问题:\(\mathcal{Y}\)有更多的类别;
- 回归:\(\mathcal{Y}=\mathbb{R}\)或\(\mathcal{Y}=[\text{lower}, \text{upper}]\subset\mathbb{R}\);
- 结构学习(Structured Learning):\(\mathcal{Y}\)是某种结构,如学习出句子的结构等。
依据数据标签\(y_n\)的不同来分:
- 监督(Supervised)学习:每个\(\mathbf{x}_n\)都有对应的\(y_n\);
- 无监督(Unsupervised)学习,没有标签\(y_n\),如聚类、密度估计、离群点检测等;
- 半监督(Semi-supervised)学习:只有一小部分数据有标签,需要充分利用无标签数据,避免代价昂贵的手动打标签;
- 强化学习(Reinforcement Learning):\(y_n\)被隐含在goodness\((\tilde{y}_n)\)中。
依据\(f\Rightarrow (\mathbf{x}_n, y_n)\)的不同来分:
- Batch:所有的数据都是已知的;
- Online:被动获取的序列数据;
- Active Learning:通过策略不断主动询问某个\(\mathbf{x}_n\)的\(y_n\)是什么,来获得序列数据。
依据输入空间\(\mathcal{X}\)的不同来分:
- 具体的(Concrete)特征:\(\mathcal{X}\subseteq \mathbb{R}^d\)的每个维度都有复杂的物理意义。
- 原始的(Raw)特征:只有简单的物理意义,如手写数字识别,特征是每个像素点的灰度,往往需要人或机器将它转换为具体的特征。
- 抽象的特征:没有或几乎没有物理意义,如打分预测系统,\(\mathcal{X}\)是用户id,\(\mathcal{Y}\)是对某部电影的评分,也需要做特征转换/抽取/构造。