pytorch框架学习（8）——nn网络层

1. 卷积层

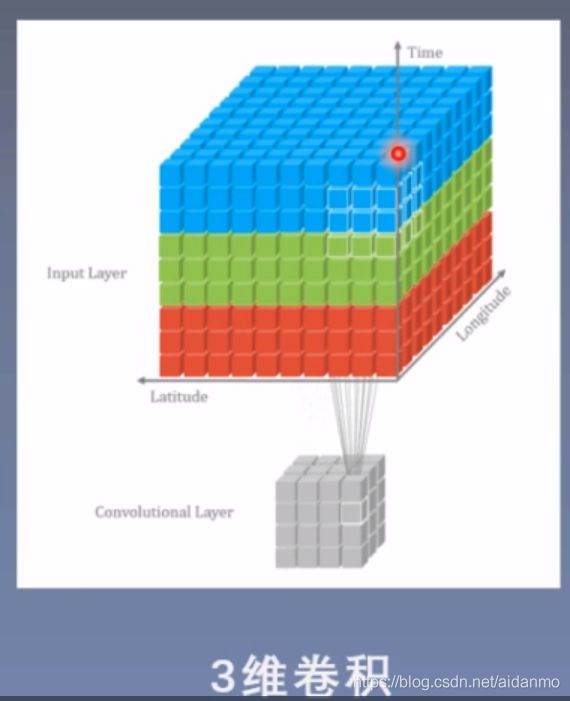
1.2 1d/2d/3d卷积

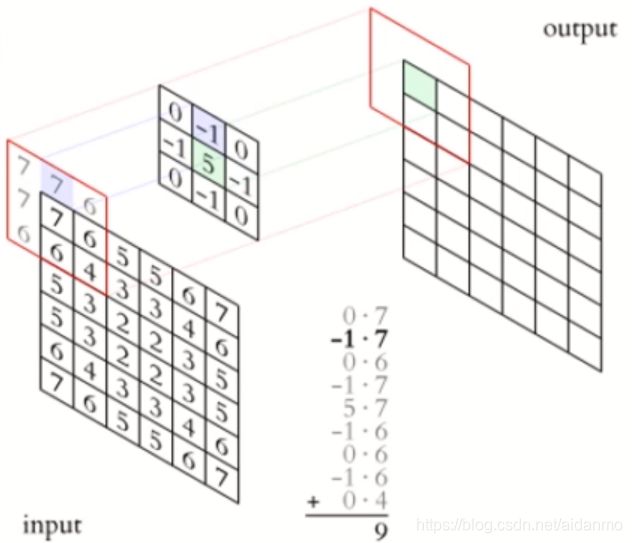
• 卷积运算：卷积核在输入信号（图像）上滑动，相应位置上进行乘加

• 卷积核：又称为滤波器，过滤器，可认为是某种模式，某种特征
  

• 卷积过程类似于用一个模板去图像上寻找与它相似的区域，与卷积核模式越相似，激活值越高，从而实现特征提取。
  
  上图是AlexNet卷积核可视化图像，发现卷积核学习到的是边缘，条纹，色彩这一些细节模式。

• 卷积维度：一般情况下，卷积核在几个维度上滑动，就是几维卷积
  

1.3 卷积-nn.Conv2d()

• nn.Conv2d
  • 功能：对多个二维信号进行二维卷积
  • in_channels：输入通道数
  • out_channels：输出通道数，等价于卷积核个数
  • kernel_size：卷积核尺寸
  • stride：步长
  • padding：填充个数
  • dilation：空洞卷积大小
  • groups：分组卷积设置
  • bias：偏置
• 尺寸计算：
  简化版：$ou{t}_{size}=\frac{I{n}_{size}-kerne{l}_{size}}{stride}+1$

# load img
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), 'lena.png')
img = Image.open(path_img).convert('RGB')

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# 创建卷积层
# 2d
flag = 1
# flag = 0
if flag:
    conv_layer = nn.Conv2d(3, 1, 3)     # input:(i, o, size)
    nn.init.xavier_normal_(conv_layer.weight.data)   # 正态分布初始化

    # calculation
    img_conv = conv_layer(img_tensor)

卷积前尺寸：torch.Size([1, 3, 512, 512])
卷积后尺寸：torch.Size([1, 1, 510, 510])

1.4 转置卷积-ConvTranspose

• 转置卷积用于对图像进项上采样
  
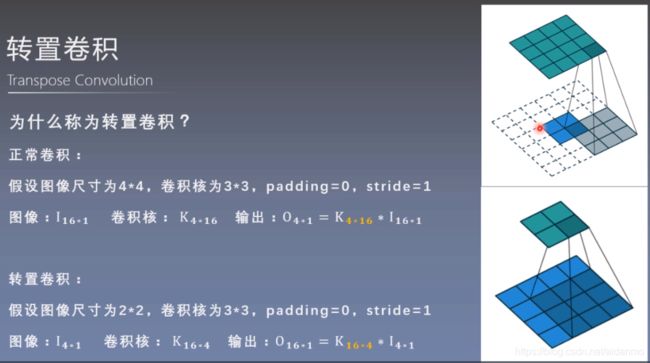
• nn.ConvTranspose2d
  • 功能：转置卷积实现上采样
  • in_channels：输入通道数
  • out_channels：输出通道数
  • kernel_size：卷积核尺寸
  • stride：步长
  • padding：填充个数
  • dilation：空洞卷积大小
  • groups：分组卷积设置
  • bias：偏置
• 尺寸计算：
  简化版: $ou{t}_{size}=(i{n}_{size}-1)\ast stride+kerne{l}_{size}$

# transposed
flag = 1
# flag = 0
if flag:
    conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2)
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

卷积前尺寸：torch.Size([1, 3, 512, 512])
卷积后尺寸：torch.Size([1, 1, 1025, 1025])

2. 池化层——Pooling Layer

• 池化运算：对信号进行“收集”并“总结”，类似水池收集水资源，因而得名池化层。
• 收集：多变少
• 总结：最大值/平均值
  
  
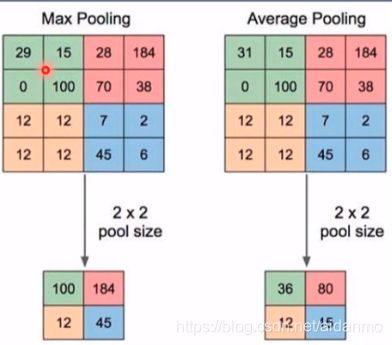
• nn.MaxPool2d
  • 功能：对二维信号进行最大值池化
  • kernel_size：池化核尺寸
  • stride：步长
  • padding：填充个数
  • dilation：池化核间隔大小
  • ceil_mode：尺寸向上取整
  • return_indices：记录池化像素索引

    maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2))
    img_pool = maxpool_layer(img_tensor)

池化前尺寸:torch.Size([1, 3, 512, 512])
池化后尺寸:torch.Size([1, 3, 256, 256])

• nn.AvgPool2d
  • 功能：对二维信号进行平均值池化
  • kernel_size：池化核尺寸
  • stride：步长
  • padding：填充个数
  • ceil_mode：尺寸向上取整
  • count_include_pad：填充值用于计算
  • divisor_override：除法因子

    avgpool_layer = nn.AvgPool2d((2, 2), stride=(2, 2))
    img_pool = avgpool_layer(img_tensor)

池化前尺寸:torch.Size([1, 3, 512, 512])
池化后尺寸:torch.Size([1, 3, 256, 256])

• nn.MaxUnpool2d（反池化）
  • 功能：对二维信号进行最大值池化上采样，根据索引进行反池化
  • kernel_size：池化核尺寸
  • stride：步长
  • padding：填充个数
    

    # pooling
    img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)
    maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)
    img_pool, indices = maxpool_layer(img_tensor)	# indices为坐标信息

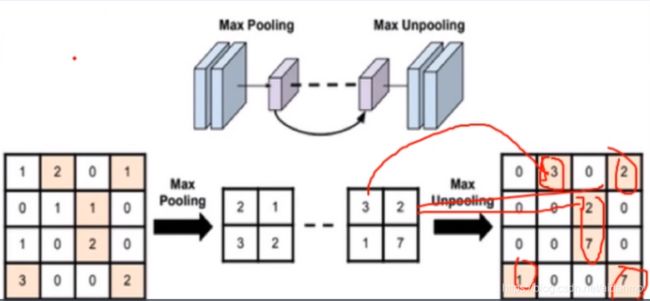
    # unpooling
    img_reconstruct = torch.randn_like(img_pool, dtype=torch.float)
    maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))
    img_unpool = maxunpool_layer(img_reconstruct, indices)

执行结果：

raw_img:
tensor([[[[0., 4., 4., 3.],
          [3., 3., 1., 1.],
          [4., 2., 3., 4.],
          [1., 3., 3., 0.]]]])
img_pool:
tensor([[[[4., 4.],
          [4., 4.]]]])
img_reconstruct:
tensor([[[[-1.0276, -0.5631],
          [-0.8923, -0.0583]]]])
img_unpool:
tensor([[[[ 0.0000, -1.0276, -0.5631,  0.0000],
          [ 0.0000,  0.0000,  0.0000,  0.0000],
          [-0.8923,  0.0000,  0.0000, -0.0583],
          [ 0.0000,  0.0000,  0.0000,  0.0000]]]])

3. 线性层——Linear Layer

• 线性层又称全连接层，其每个神经元与上一层所有神经元相连，实现对前一层的线性组合，线性变换。
  
  计算方式如下：
  
• nn.Linear
  • 功能：对一维信号（向量）进行线性组合
  • in_features：输入结点数
  • out_features：输出结点数
  • bias：是否需要偏置
  • 计算公式：$y=x{W}^T+bias$

    inputs = torch.tensor([[1., 2, 3]])
    linear_layer = nn.Linear(3, 4)
    linear_layer.weight.data = torch.tensor([[1., 1., 1.],
                                             [2., 2., 2.],
                                             [3., 3., 3.],
                                             [4., 4., 4.]])

    linear_layer.bias.data.fill_(0.5)
    output = linear_layer(inputs)
    print(inputs, inputs.shape)
    print(linear_layer.weight.data, linear_layer.weight.data.shape)
    print(output, output.shape)

结果为：

tensor([[1., 2., 3.]]) torch.Size([1, 3])
tensor([[1., 1., 1.],
        [2., 2., 2.],
        [3., 3., 3.],
        [4., 4., 4.]]) torch.Size([4, 3])
tensor([[ 6.5000, 12.5000, 18.5000, 24.5000]], grad_fn=<AddmmBackward>) torch.Size([1, 4])

4. 激活函数层——Activation Layer

• 激活函数对特征进行非线性变换，赋予多层神经网络具有深度的意义。
  
  如果没有激活函数层，那么多个线性层的叠加相当于一个线性层。
• nn.Sigmoid
  • 公式：$y=\frac{1}{1+e^{-x}}$
  • 梯度公式：KaTeX parse error: Expected group after '^' at position 2: y^̲' = y * (1-y)
  • 特性：
    1. 输出值在（0,1），符合概率
    2. 导数范围[0, 0.25]，易导致梯度消失
    3. 输出为非0均值，破坏数据分布
       
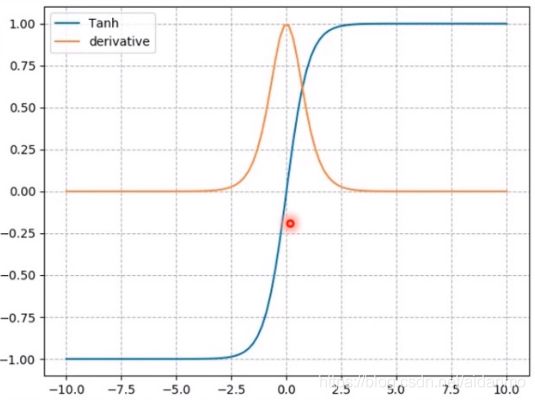
• nn.tanh
  • 公式：$y=\frac{sinx}{cosx}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{2}{1+e^{-2x}}+1$
  • 梯度公式：KaTeX parse error: Expected group after '^' at position 2: y^̲' = 1-y^2
  • 特性：
    1. 输出值在（-1,1），数据符合0均值
    2. 导数范围是（0,1），易导致梯度消失
       
       为了解决梯度消失的问题，提出了nn.ReLU（修正线性单元）
• nn.ReLU
  • 公式：$y=max(0,x)$
  • 梯度公式：$f(x)=\{\begin{array}{ll}1& \text{x>0}\\ undefined& \text{x=0}\\ 0& \text{x<0}\end{array}$
  • 特性：
    1. 输出值均为正数，负半轴导致死神经元
    2. 导数是1，缓解梯度消失，但是容易引发梯度爆炸
       
       3中改进的ReLU
• nn.LeakyReLU
  • negative_slope:负半轴斜率
• nn.PReLU
  • init：可学习斜率
• nn.RReLU
  • lower：均匀分布下限
  • upper：均匀分布上限