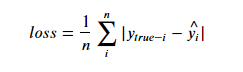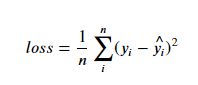如何从0-1构建自己的”pytorch“(自己专属的深度学习框架)——part01
整体学习目标
- 建立属于你自己的深度学习框架
- Python创建线性回归模型,L1损失函数,L2损失函数
- 参数初始化
- 掌握梯度下降算法,创建优化器函数
- 学会设置学习率以避免梯度爆炸
- 掌握多个常用激活函数,Sigmoid, Relu,Tanh,Leaky_Relu,避免梯度消失
- 掌握链式法则,计算图,拓扑,前馈/反向网络
创建线性回归模型
概念:首先该模型主要解决的情况是:你有一堆线性数据,你需要根据已知的样本数据,去拟合出一个模型或者说一条线,这样当你有新的数据点的时候,你就可以根据之前拟合出的模型也就是线,来进行预测,比如根据房屋面积来预测房价。
解析:
- 你要寻找到一条线,你就需要知道这条线的斜率k和截距b,这样你才能画出这条线
- 如何找到或者说怎么算好的斜率k和截距b(也就是我们常说的参数),你需要损失函数,对应的损失函数越小,证明参数越好
- 损失函数可以选则,L2-loss和L1-loss,一会儿后面会解释什么是l1和l2
- 然后你还需要梯度下降法来更新参数即可
- 如下图,左图为l1-loss,右图为l2-loss
整体流程:
随机初始化参数,斜率k和截距b,然后通过y=kx+b这一公式,将样本点(x,y)中的x带入,然后会得到一个预测值y_predict,通过损失函数获得损失值,然后再反向梯度求导,获得参数的更新值,即可完成参数一次更新。
代码:
#Linear-regression 线性回归代码
#加载数据,波士顿-房价预测数据
from sklearn.datasets import load_boston
data = load_boston()
#这是对应的训练数据,X和y
X, y = data['data'], data['target']
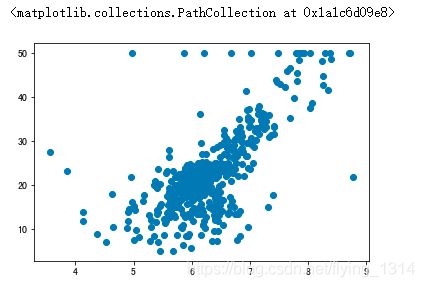
#将数据以散点图呈现,这里X数据有13个特征,我们只用了第5个特征,room_size,也就是房间面积
%matplotlib inline
import matplotlib.pyplot as plt
plt.scatter(X[:, 5], y)
画出的散点图如下:
#定义损失函数,来衡量参数是否好,这里是l2-loss
def loss(y, y_hat):
sum_ = sum([(y_i - y_hat_i) ** 2 for y_i, y_hat_i in zip(y, y_hat)])
return sum_ / len(y)
#下面是分别对k和b求梯度,这样保证每次,k和b都能朝着loss减小的方向更新
def partial_k(x, y, y_hat):
gradient = 0
for x_i, y_i, y_hat_i in zip(list(x), list(y), list(y_hat)):
gradient += (y_i - y_hat_i) * x_i
return -2 / len(y) * gradient
def partial_b(y, y_hat):
gradient = 0
for y_i, y_hat_i in zip(list(y), list(y_hat)):
gradient += (y_i - y_hat_i)
return -2 / len(y) * gradient#最后训练即可
#该函数计算房价
def price(x, k, b):
# Operation : CNN, RNN, LSTM, Attention 比KX+B更复杂的对应关系
return k*x + b
#训练次数
trying_times = 50000
#初始loss值
min_cost = float('inf')
losses = []
scala = 0.3
# 参数初始化问题! Weight Initizalition 问题!这也是一个大问题,这里我们先这样
k, b = random.random() * 100 - 200, random.random() * 100 - 200
best_k, best_b = None, None
#学习率
learning_rate = 1e-3 # Optimizer Rate
for i in range(trying_times):
price_by_random_k_and_b = [price(r, k, b) for r in X_rm]
cost = loss(list(y), price_by_random_k_and_b)
if cost < min_cost:
# print('在第{}, k和b更新了'.format(i))
min_cost = cost
#获得最好的k和b
best_k, best_b = k, b
losses.append((i, min_cost))
#获得参数需要更新的梯度
k_gradient = partial_k(X_rm, y, price_by_random_k_and_b) # 变化的方向
b_gradient = partial_b(y, price_by_random_k_and_b)
#更新参数
k = k + (-1 * k_gradient) * learning_rate
## 优化器: Optimizer 这块也是一个研究方向
## Adam 动量 momentum
b = b + (-1 * b_gradient) * learning_rate总结
至此,我们就完成了线性回归模型,大家感兴趣可以去尝试将loss函数修改成l1-loss并进行调试,降低loss,欢迎大家随时交流后,后面会陆续把这个部分更完,此次内容来自开课吧的训练营。