Methods for Vehicle Scheduling in PT System

//Author: 宋绪杰 @ BJTU

在Public Transport System中，存在如何调度车辆使得所需车辆总数(fleet size)最少的问题。本文设计3种图论算法解决以上问题，作为“Planing & Operating Public Transport Systems”课程大作业的一部分。同时也在“交通网络分析与设计”Assignment 7中使用。

Method	Node	Model	Solver	Time complexity	Remark
1	End/Start time (终到/出发时间)	Max. bipartite matching (最大二分图匹配)	Hungarian Algorithm (匈牙利算法)	O(n*m)
2	End/Start time (终到/出发时间)	Max. flow (最大流)	Ford-Fulkerson(EK) / Dinic	O(n^2*m)
3	End/Start time (终到/出发时间)	Max. flow with min. cost (最小费用最大流)	EK+Dijkstra+Heap (EK+堆优化Dijkstra)	O(f*m*log(n))	with min. DH trips (允许空载且次数最少)

Method 1

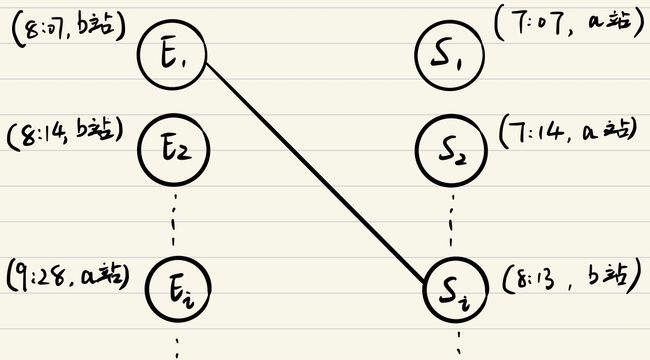
在Method1中，图中节点被分为两类，左边一类节点仅包含trips的终到时间，右边一列节点仅包含trips的出发时间，同时每个节点记录了对应此时间的站名（a站/b站）。
若两个节点Ei和Sj满足以下条件，则表明trip j能接续trip i，那么在Ei和Sj间连一条边，称作左边的节点Ei和右边的节点Sj“匹配”。

1. Ei和Sj所在站一致
2. Sj的出发时间晚于Ei的到达时间

且每个点最多只能和一个点匹配（仅能接续/被接续一次），同类节点不能匹配。
初始有N个trips待安排，最差情况下一辆车跑一个trip则需N辆车；图中每多一个匹配，则可以少用一辆车。即：Min fleet size = N - 最大匹配数。

经典的二分图匹配问题，用匈牙利算法即可求解。
时间复杂度O(n*m)，其中n为点数，m为可匹配的边数。

Method 2

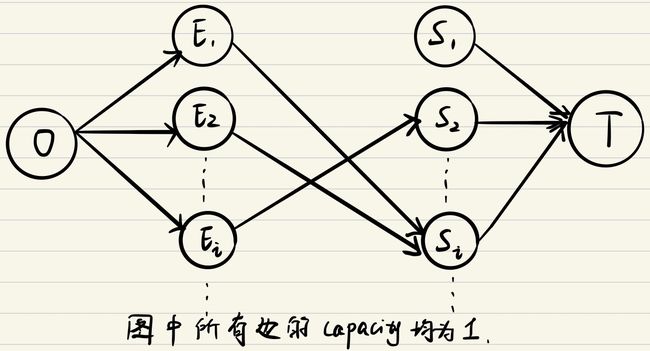
Method2将Method1的建图做如下转化，使其能够用网络流算法求解。

1. 建立一个源点O、一个汇点T。
2. 将Method1中的边改为有向边，方向为Ei -> Sj，且设置其容量(capacity)为1。
3. 从O向所有Ei顶点连一条容量为1的有向边。
4. 从所有Sj顶点向T连一条容量为1的有向边。

因为节点流量守恒，所以通过设置容量为1即可限制每一Ei/Sj顶点不可接续/被接续多次。
则从O向T的最大流等价于Method1中最大匹配数。即：Min fleet size = N - 最大流。

经典的最大流问题，用Ford-Fulkerson(Edmonds-Karp) / Dinic即可求解。
Dinic由于采用分层图、多路增广等策略，时间复杂度比其他网络流算法较优，因此这里使用Dinic。
使用Dinic的时间复杂度为O(n^2*m)，其中n为点数，m为边数。

Method 3

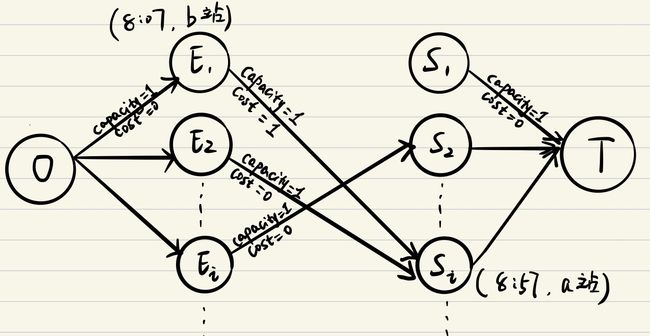
Method3相比Method2而言，不但允许DH trips，而且可以使得在fleet size最小的情况下DH trips的数量最少。
若点Ei和Sj满足以下条件之一，则表明trip j能接续trip i，那么由Ei向点Sj连一条容量为1的有向边。

1. （普通接续）点Ei的终到站是点Sj的出发站，且Ei的终到时间早于Sj的出发时间。
2. （DH 接续）点Ei的终到站不是点Sj的出发站，但Ei的终到时间+DH time<=Sj的出发时间。
   （注：Method1、Method2也可通过此种建图方法考虑DH trips，但不能保证DH trips最少。为了简化未在前两个Method中使用。）

若为“普通接续”边，设置此边的cost为0；若为“DH接续”边，设置此边的cost为1。
建立源点O和汇点T，由O分别向每个Ei连接一条容量为1、cost为0的有向边，由每个Sj分别向T连接一条容量为1、cost为0的有向边。
然后求O->T的最小费用最大流。则Min fleet size = N - 最大流，DH trips数量 = 总最小费用。

经典的最小费用最大流问题，用Dinic+堆优化的Dijkstra即可求解。
时间复杂度为O(f*m*log(n))，其中f为最大流量，n为点数，m为边数。

实验结果

Method 1

Method 2

Method 3

Code

//Author: 宋绪杰 17252048 @ BJTU

#include 
using namespace std;

typedef long long llong;
const int tmax=1005;

int na,nb;//上下行trips数量
int start_time[2][tmax],end_time[2][tmax];
int father[tmax],child[tmax];//前驱后继

void print(int x)
{
    if(x<=na)
        printf("[%02d:%02d,a -> %02d:%02d,b]",start_time[0][x]/60,start_time[0][x]%60,end_time[0][x]/60,end_time[0][x]%60);
    else
        printf("[%02d:%02d,b -> %02d:%02d,a]",start_time[1][x-na]/60,start_time[1][x-na]%60,end_time[1][x-na]/60,end_time[1][x-na]%60);
    
    if(child[x]!=0)
    {
        printf(" -> ");
        print(child[x]);
    }
    
    return;
}

//-------Method 1----------
int s[tmax],ans;
bool mmap[tmax][tmax],v[tmax];

bool dfs(int x)
{
    int i;
    
    for(i=1;i<=na+nb;i++)
    {
        if(!v[i]&&mmap[x][i])
        {
            v[i]=true;
            if(s[i]==0||dfs(s[i]))
            {
                s[i]=x;
                return true;
            }
        }
    }
    
    return false;
}
void Hungarian()
{
    ans=0;
    
    memset(s,0,sizeof(s));
    memset(mmap,0,sizeof(mmap));
    
    for(int i=1;i<=na;i++)
        for(int j=1;j<=nb;j++)
    {
        if(start_time[1][j]>=end_time[0][i])
            mmap[i][na+j]=true;
        if(start_time[0][i]>=end_time[1][j])
            mmap[na+j][i]=true;
    }

    for(int i=1;i<=na+nb;i++)
    {
        memset(v,0,sizeof(v));
        if(dfs(i)) ans++;
    }

    printf("\n-------Answer of Method 1-------\n\n");
    printf("Min. fleet size = %d.\n",na+nb-ans);
    
    int num=0;
    
    memset(father,0,sizeof(father));
    memset(child,0,sizeof(child));
    
    for(int i=1;i<=na+nb;i++)
        if(s[i]!=0)
        {
            father[i]=s[i];
            child[s[i]]=i;
        }
    
    for(int i=1;i<=na+nb;i++)
        if(father[i]==0)
        {
            printf("\nChain #%d: ",++num);
            print(i);
        }
    printf("\n--------------------------------\n\n");
    return;
}
//-------------------------

//-------Method 2----------
const int inf_int=1e9+5;
const llong inf=1e16;

struct edge2{
    int to,cap,rev;
};

vector<edge2> G[tmax];
int level[tmax],iter[tmax];

void add(int from,int to,int cap)
{
    G[from].push_back((edge2){to,cap,G[to].size()});
    G[to].push_back((edge2){from,0,G[from].size()-1});
    return;
}

void bfs(int s)
{
    memset(level,-1,sizeof(level));

    queue<int> que;
    level[s]=0;
    que.push(s);

    while(!que.empty())
    {
        int v=que.front();
        que.pop();

        for(int i=0;i<G[v].size();i++)
        {
            edge2 &e=G[v][i];
            if(e.cap>0&&level[e.to]<0)
            {
                level[e.to]=level[v]+1;
                que.push(e.to);
            }
        }
    }

    return;
}

int dfs2(int v,int t,int f)
{
    if(v==t) return f;

    for(int &i=iter[v];i<G[v].size();i++)
    {
        edge2 &e=G[v][i];

        if(e.cap>0&&level[v]<level[e.to])
        {
            int d=dfs2(e.to,t,min(f,e.cap));

            if(d>0)
            {
                e.cap-=d;
                G[e.to][e.rev].cap+=d;
                return d;
            }
        }
    }
    return 0;
}

void Dinic()
{
    for(int i=1;i<=na;i++)
        for(int j=1;j<=nb;j++)
    {
        if(start_time[1][j]>=end_time[0][i])
            add(i,na+nb+na+j,1);

        if(start_time[0][i]>=end_time[1][j])
            add(na+j,na+nb+i,1);
    }

    for(int i=1;i<=na+nb;i++)
    {
        add(0,i,1);
        add(na+nb+i,na*2+nb*2+1,1);
    }

    int flow=0;
    while(1)
    {
        bfs(0);
        if(level[na*2+nb*2+1]<0) break;

        memset(iter,0,sizeof(iter));

        int f;
        while((f=dfs2(0,na*2+nb*2+1,inf_int))>0)
            flow+=f;
    }

    printf("\n-------Answer of Method 2-------\n\n");
    printf("Min. fleet size = %d.\n",na+nb-flow);

    int num=0;
    memset(father,0,sizeof(father));
    memset(child,0,sizeof(child));

    for(int i=1;i<na+nb;i++)
        for(int j=0;j<G[i].size();j++)
            if(G[i][j].cap==0&&G[i][j].to!=0)
            {
                father[G[i][j].to-na-nb]=i;
                child[i]=G[i][j].to-na-nb;
            }

    for(int i=1;i<=na+nb;i++)
        if(father[i]==0)
        {
            printf("\nChain #%d: ",++num);
            print(i);
        }
    printf("\n--------------------------------\n\n");

    return;
}
//-------------------------

//-------Method 3----------
const int INF = 0x7fffffff;
int k,data[tmax];

struct edge {
	int to, capacity, cost, rev;
	edge() {}
	edge(int to, int _capacity, int _cost, int _rev) :to(to), capacity(_capacity), cost(_cost), rev(_rev) {}
};

struct Min_Cost_Max_Flow
{
	int V, H[tmax + 5], dis[tmax + 5], PreV[tmax + 5], PreE[tmax + 5];
	vector<edge> G[tmax + 5];

	//调用前初始化
	void Init(int n)
	{
		V = n;
		for (int i = 0; i <= V; ++i)G[i].clear();
	}

	//加边
	void Add_Edge(int from, int to, int cap, int cost) 
	{
		G[from].push_back(edge(to, cap, cost, G[to].size()));
		G[to].push_back(edge(from, 0, -cost, G[from].size() - 1));
	}

	//flow是自己传进去的变量，就是最后的最大流，返回的是最小费用
	int Min_cost_max_flow(int s, int t, int f, int& flow) 
	{
		int res = 0; fill(H, H + 1 + V, 0);

		while (f)
		{
			priority_queue <pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > q;
			fill(dis, dis + 1 + V, INF);
			dis[s] = 0; q.push(pair<int, int>(0, s));

			while (!q.empty()) {
				pair<int, int> now = q.top(); q.pop();
				int v = now.second;

				if (dis[v] < now.first)continue;

				for (int i = 0; i < G[v].size(); ++i) 
				{
					edge& e = G[v][i];

					if (e.capacity > 0 && dis[e.to] > dis[v] + e.cost + H[v] - H[e.to]) 
					{
						dis[e.to] = dis[v] + e.cost + H[v] - H[e.to];
						PreV[e.to] = v;
						PreE[e.to] = i;
						q.push(pair<int, int>(dis[e.to], e.to));
					}
				}
			}

			if (dis[t] == INF)break;
			for (int i = 0; i <= V; ++i)H[i] += dis[i];

			int d = f;
			for (int v = t; v != s; v = PreV[v])d = min(d, G[PreV[v]][PreE[v]].capacity);
			f -= d; flow += d; res += d*H[t];

			for (int v = t; v != s; v = PreV[v]) {
				edge& e = G[PreV[v]][PreE[v]];
				e.capacity -= d;
				G[v][e.rev].capacity += d;
			}
		}

		return res;
	}
};

void EK()
{
    Min_Cost_Max_Flow Network;
    Network.Init(na*2+nb*2+2);

    for(int i=1;i<=na;i++)
        for(int j=1;j<=nb;j++)
    {
        if(start_time[1][j]>=end_time[0][i])
            Network.Add_Edge(i,na+nb+na+j,1,0);
        if(start_time[0][i]>=end_time[1][j])
            Network.Add_Edge(na+j,na+nb+i,1,0);
    }

    for(int i=1;i<=na;i++)
        for(int j=1;j<=na;j++)
    {
        if(i==j) continue;
        if(start_time[0][j]>=end_time[0][i]+20)
            Network.Add_Edge(i,na+nb+j,1,1);
    }

    for(int i=1;i<=nb;i++)
        for(int j=1;j<=nb;j++)
    {
        if(i==j) continue;
        if(start_time[1][j]>=end_time[1][i]+20)
            Network.Add_Edge(na+i,na+nb+na+j,1,1);
    }

    for(int i=1;i<=na+nb;i++)
    {
        Network.Add_Edge(0,i,1,0);
        Network.Add_Edge(na+nb+i,na*2+nb*2+1,1,0);
    }

    int flow=0;
    int sum_cost=Network.Min_cost_max_flow(0,na*2+nb*2+1,INF,flow);

    printf("\n-------Answer of Method 3-------\n\n");
    printf("Min. fleet size = %d with %d DH trips.\n",na+nb-flow,sum_cost);

    int num=0;
    memset(father,0,sizeof(father));
    memset(child,0,sizeof(child));

    for(int i=1;i<na+nb;i++)
        for(int j=0;j<Network.G[i].size();j++)
            if(Network.G[i][j].capacity==0&&Network.G[i][j].to!=0)
            {
                father[Network.G[i][j].to-na-nb]=i;
                child[i]=Network.G[i][j].to-na-nb;
            }

    for(int i=1;i<=na+nb;i++)
        if(father[i]==0)
        {
            printf("\nChain #%d: ",++num);
            print(i);
        }

    printf("\n--------------------------------\n\n");

    return;
}
//-------------------------

void init()
{
    int full_time[2]={0,0};

    printf("请输入上行平均全程时间(min):");
    scanf("%d",&full_time[0]);
    printf("请输入上行发车数量:");
    scanf("%d",&na);
    printf("请输入%d个发车时间:",na);

    int hh,mm;
    for(int i=1;i<=na;i++)
    {
        scanf("%d:%d",&hh,&mm);
        start_time[0][i]=hh*60+mm;
        end_time[0][i]=start_time[0][i]+full_time[0];
    }

    printf("\n请输入下行平均全程时间(min):");
    scanf("%d",&full_time[1]);
    printf("请输入下行发车数量:");
    scanf("%d",&nb);
    printf("请输入%d个发车时间:",nb);

    for(int i=1;i<=nb;i++)
    {
        scanf("%d:%d",&hh,&mm);
        start_time[1][i]=hh*60+mm;
        end_time[1][i]=start_time[1][i]+full_time[1];
    }
    return;
}

int main()
{
    printf("//Author: 宋绪杰 @ BJTU\n");

    while(1)
    {
        printf("\n-------------选择模式-----------\n\n");
        printf("Method 1: 最大二分图匹配 ( 匈牙利算法 ) \n");
        printf("Method 2: 最大流 ( Dinic算法 ) \n");
        printf("Method 3: 最小费用最大流 ( EK+Dijkstra+Heap ) - Enable DH trips\n");
        printf("\n--------------------------------\n\n");

        int kase=1;

        printf("选择模式：");
        scanf("%d",&kase);

        system("clear");

        switch(kase)
        {
        case 1:
            printf("\n已进入Method 1: 最大二分图匹配 ( 匈牙利算法 ) \n\n");
            init();
            Hungarian();
            break;

        case 2:
            printf("\n已进入Method 2: 最大流 ( Dinic算法 ) \n\n");
            init();
            Dinic();
            break;

        case 3:
            printf("\n已进入Method 3: 最小费用最大流 ( EK+Dijkstra+Heap ) - Enable DH trips \n\n");
            init();
            EK();
            break;

        default:
            printf("\n请输入正确的序号\n");
        }

    }

    return 0;
}