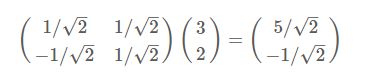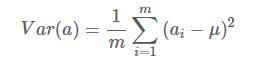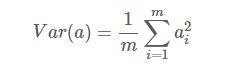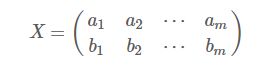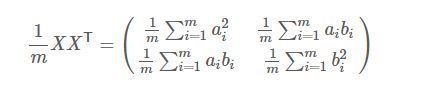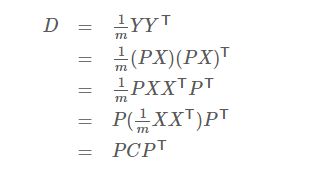PCA(主成分分析-principal components analysis)学习笔记以及源代码实战讲解
PCA(主成分分析-principal components analysis)学习笔记以及源代码实战讲解
文章目录
- PCA(主成分分析-principal components analysis)学习笔记以及源代码实战讲解
- 前言
- PCA(主成分分析) 原理分析
- PCA 是什么？
- PCA优点
- PCA原理（主要涉及线性代数得的知识，大家耐心看）
- 代码解读
前言
在看完吴恩达讲解的PCA(主成分分析)方法后，想着能够用代码的方式实践一下。紧接着就借阅了一下《机器学习实战》里面对PCA的流程的讲解和代码。现在对PCA的运算过程还是比较明白的，也希望这份学习笔记能够帮助刚开始学习PCA的同学们。
源代码已上传到github，有需要的同学可以去下载，别忘了给个⭐哦
源代码地址
PCA(主成分分析) 原理分析
-
PCA 是什么？
PCA即主成分分析，是一种数据降维的方法，可以将多指标转化为少指标。这里举个例子吧，在我们使用数据做分析前，需要对数据进行一系列的处理。假如我们手上有一组房屋数据，房屋指标分别有建筑面积、实际面积、长、宽等等。这些指标中，建筑面积和实际面积之间有很强的正相关性，那也就说，我们其实可以使用一个指标来取代这两个指标。
-
PCA优点
- 能够降低算法的计算开销。我们在使用深度网络训练模型时，使用1000层网络消耗的计算资源远远大于100层消耗的资源。
- 能够去除一些噪声。PCA的思想就决定了我们所取得特征都是能够尽可能区分数据得特征，在我们得数据中，有一些指标并没有实际作用。
- 使得数据集更易使用。
-
PCA原理（主要涉及线性代数得的知识，大家耐心看）
内积：也称数量积，两个向量对应元素的的乘积之和百度百科-内积。计算很简单，但是我们这里说一下它在几何中的作用。看下面这张图：
这里有两个向量，分别是向量A和向量B，二者的内积为：A·B = |A| ·|B|·cos(a)
这里我们令B向量为单位向量(或模长为1)，即|B|=1，所以有A·B = |A|·cos(a)
此时结果等于向量A在向量B上的投影长度。
也就是说当B向量的模长为1时，A与B的内积等于向量A在向量B上的投影的长度
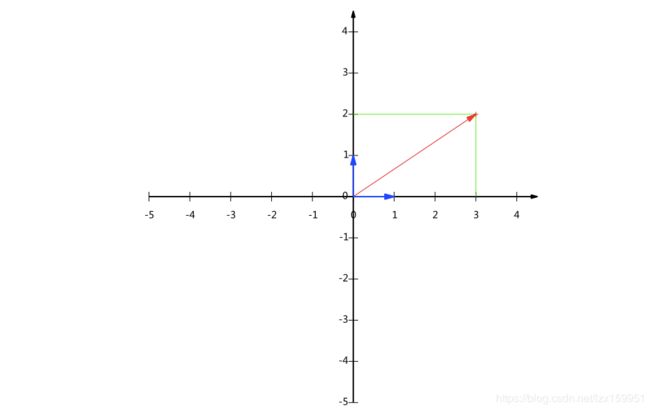
坐标轴的基：在我们平常见到的x-y坐标轴，(1,0)和(0,1)为该坐标轴的一组基。坐标轴上的任意一个向量都能够用这与一组基来表示。
图中的向量为(3,2)，可以用两个(0,1)和三个(1,0)来表示。我们将这个向量分别向这两个基做投影，所得到的投影的长度就是我们可以用来表示的数量。
前面的内积公式大家没忘记吧，A**·B = |A|·|B|·**cos(a) 。我们令B向量为一个基(1,0)，A向量为图中(3,2)。
A**·B = |A|·**cos(a)=3.
也就是说，只要我们确定一组基，给出向量在这组基上的投影长度，就能够描述这个向量。
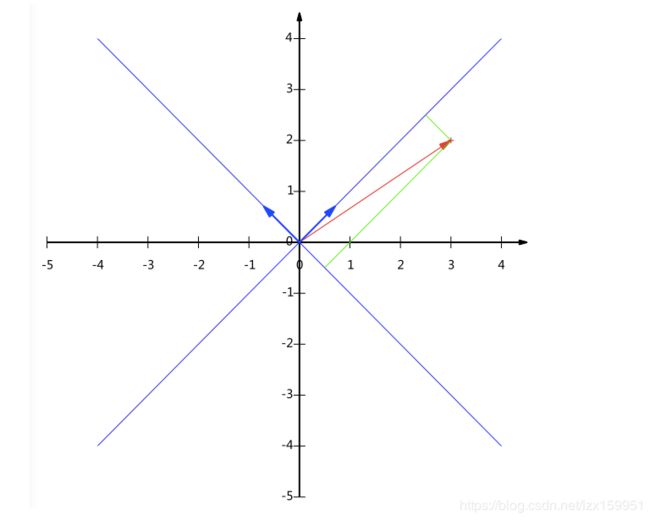
前面我们给出的是一组默认基，咱们接下来将(1,1)和（-1,1）作为一组基。因为我们想使基的模长为1，所以我们分别除以其模长。上面的基可以变为
( 1 2 , 1 2 ) \left ( \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right ) (21,21)
和
( − 1 2 , 1 2 ) \left ( -\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right ) (−21,21)
接下来，咱们根据给出的这一组基来表示向量(3,2)：
在这组基上得投影长度分别为：
( 3 , 2 ) ⋅ ( 1 2 , 1 2 ) = 5 2 \left (3,2 \right )\cdot \left ( \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right )=\frac{5}{\sqrt{2}} (3,2)⋅(21,21)=25
( 3 , 2 ) ⋅ ( − 1 2 , 1 2 ) = − 5 2 \left (3,2 \right )\cdot \left ( -\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right )=-\frac{5}{\sqrt{2}} (3,2)⋅(−21,21)=−25
所以向量(3，2)在新基表示为:
( 5 2 , − 5 2 ) \left ( \frac{5}{\sqrt{2}} ,-\frac{5}{\sqrt{2}}\right ) (25,−25)
整体流程可以写成如下形式：
左边为基矩阵，每一行为一个基坐标，右边为需要转化得列向量，等号右边为转化后得列向量。
我们再接着扩展，使用数学通式来表示：
**协方差：**用来衡量两个变量的总体误差。直观上来说，就是如果两个变量的变化趋势一致，协方差为正值，变换趋势不一致，则为负值。方差是协方差的一种特殊形况(两个变量相同)
方差公式：
μ为a的均值
协方差公式：
C o n ( a , b ) = ∑ i − 1 m ( a i − μ 1 ) ⋅ ( b i − μ 2 ) Con(a,b)=\sum_{i-1}^{m}\left (ai-\mu 1 \right )\cdot \left ( bi-\mu 2 \right ) Con(a,b)=i−1∑m(ai−μ1)⋅(bi−μ2)
μ1为a的均值，μ2为b的均值
**协方差矩阵：**协方差矩阵得每个元素是各个向量元素之间的协方差。那么，什么是协方差呢？
这里我们可以将向量提前处理：我们将每个字段减去其平均值。
即方差公式可写成：
协方差公式可写成：
我们还是使用上面a、b两个字段
然后我们将X乘以X的转置，再除以m得：
很明显，右侧得矩阵就是我们需要得协方差矩阵。
所以，我们可以得出一般得结论：
优化目标：
我们如果将二维数据降维到一维，如何能够减少数据损失呢(在一维上也能够准确的分辨出各个数据)，就是使得数据足够分散。这里有个指标，用来衡量数据得分散程度的，叫做方差。方差越大，数据分散的越大。
现在我们就将问题转化为找到能令数据方差最大的那条直线(基)。
对于多维度问题来说，我们需要做的与二维转一维类似，需要找到前K个方差能令数据方差最大的基。
所找的基有什么关系呢？ 跟我们默认的一组基[(0,1),(1,0)],我们需要基之间相互正交，只有这样，这些基之间完全独立，不存在任何的线性关系。因为我们想用最少的字段来尽可能准确的描述数据，具有线性关系显然不符合我们的目标。
协方差矩阵对角化：
由上可知，协方差矩阵是一个实对称矩阵什么是实对称矩阵 ？
那么，在线性代数中，实对称矩阵有有一些比较重要的性质：
- 实对称矩阵A的不同特征值对应的特征向量是正交的。
- n阶实对称矩阵A必可相似对角化，且相似对角阵上的元素即为矩阵本身特征值。
我们假设实对称矩阵的秩为λ，那么实对称矩阵一定可以写成如下形式：
q ⋅ C ⋅ q T = ( λ 1 . . . . . . . . . λ 2 . . . . . . . . . λ 3 ) q\cdot C\cdot q^{T}=\begin{pmatrix} \lambda 1 & ... &... \\ ... & \lambda 2 & ...\\ ...& ... & \lambda 3 \end{pmatrix} q⋅C⋅qT=⎝⎛λ1.........λ2.........λ3⎠⎞
这里q是特征向量，q中的任意两个列特征向量正交。
假设我们的原数据是X，P为一组基，Y为数据X在P上的坐标。
即Y=PX。我们令X的协方差矩阵为C，Y的协方差矩阵为D，则有如下推导式：
所以，我们的任务就是寻找矩阵P
这里的D除对角线之外的值为0，对角线上的值为数据在对应特征向量上的方差值。
所以，这里的P不是别的，就是协方差矩阵的特征向量矩阵。
ok，到这里整个推导就结束了，我们使用文字来简述一下流程：
- 对数据X进行取平均值(均值为0)
- 计算数据X的协方差矩阵C。
- 计算写协方差矩阵的特征向量和特征值
- 对特征进行从大到小排序，选取前K个
- 将选取的特征值所对应的特征向量构成P
- 计算PX，即可得出新空间下的数据。
代码解读
- 加载数据
def loadDateSet(filename,delim='\t'):
with open(filename,'r')as f:
stringarr = [line.strip().split(delim) for line in f.readlines()]
datarr = [list(map(float,line)) for line in stringarr]
return np.mat(datarr)
文件中的数据：
这里我们使用的数据有两个字段，相当于将二维转一维。
- PCA主体程序
def pca(dataMat,topNfeat=99):
meanVals = np.mean(dataMat,axis=0)#计算每一个属性的均值
meanRemoved = dataMat-meanVals#将数据进行零均值化
covMat = np.cov(meanRemoved,rowvar=False)#计算协方差矩阵，rowvar=False 表示属性在列，数据在行
eigVals,eigVects = np.linalg.eig(np.mat(covMat))#计算矩阵的特征值和特征向量
#print("特征值：",eigVals)
#print("特征向量：",eigVects)
eigValInd = np.argsort(eigVals)#将特征值进行排序,按照从小到大的顺序，返回索引值
print("排序后的特征值：",eigValInd)
#这里就是取前K个最大值
eigValInd = eigValInd[:-(topNfeat+1):-1] #这里使用了切片，只取前K个最大的索引，这里我们K=1
#print("eigValInd:",eigValInd)
redEigVects = eigVects[:,eigValInd] #取特征值对应的特征向量
print("redEigVects",redEigVects)
#Y=XP
lowDDataMat = meanRemoved*redEigVects #零均值的数据与 特征向量做相乘 结果为Y,降维后的数据
#redEigVects.T 为对redEigVects 进行转置
#这里为何能还原呢，是因为P是特征向量，特征向量P*其转置=E so XP*PT=X
reconMat = (lowDDataMat*redEigVects.T)+meanVals #数据还原
return lowDDataMat,reconMat
返回值 第一个lowDDataMat 是降维后的数据，reconMat 是验证数据，在程序的最后一个语句中，将降维后的数据进行还原，以此来验证算法的正确性。
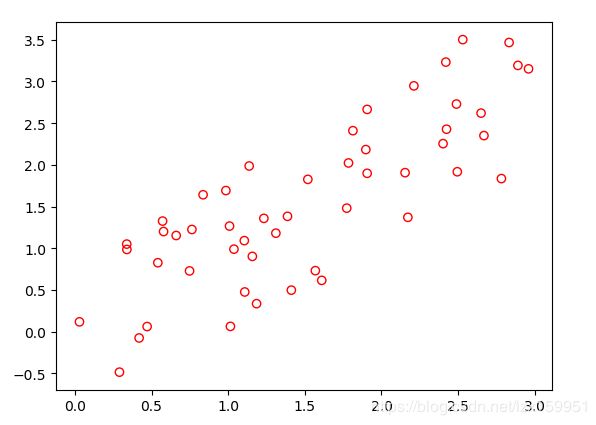
原数据图像：
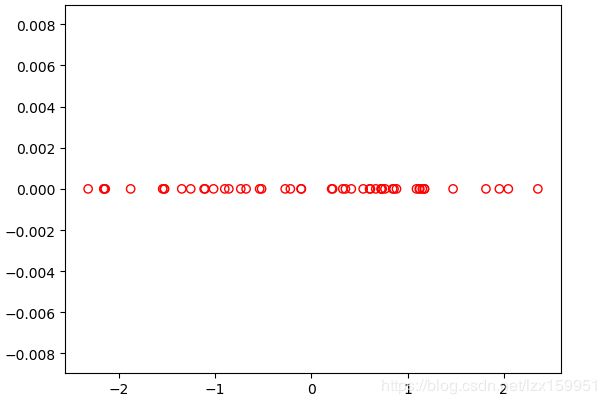
降维后的数据图像：
参考资料：
-
PCA的数学原理
-
实对称矩阵
-
协方差
十分感谢前辈们宝贵的学习笔记，让我少走了很多弯路，非常感谢，希望我也能给刚入门朋友的带来一些帮助^ v ^！