数据分析笔记:广州市财政收入挖掘预测案例
1、背景
在我国现行的分税制财政管理体制下,地方财政收入不仅是国家财政收入的重要组成部分,而且具有其相对独立的构成内容。地方财政收入是区域国民经济的综合反映,也是市场经济国家的政府进行宏观调控的基础。科学、合理地预测地方财政收人,对于克服年度地方预算收支规模确定的随意性和盲目性,正确处理地方财政与经济的相互关系具有十分重要的意义。
广州市作为广东省的省会,改革开放的前沿城市,交通便利,拥有中国大陆三大国际航空枢纽机场之一的广州白云国际机场和中国第三大港口、港口货物吞吐量居世界港口第五位的广州港。广州号称千年商埠,历史上一直是中国最重要的商业中心之一,商业网点多、行业齐全、辐射面广、信息灵、流通渠道通顺,拥有商业网点10万多个,为中国十大城市之冠。广州市在实现经济快速发展,地区生产总值飞跃的同时,也意味着财政收入的增收。2013年,广州实现地区生产总值(GDP)15420.14亿元,增长11.6%。其中,第一产业增加值228.87亿元,增长2.7 %;第二产业增加值5227.38亿元,增长9.2%;第三产业增加值9963.89亿元,增长13.3%。第一、二、三产业增加值的比例为1.48∶33.90∶64.62。三次产业对经济增长的贡献率分别为0.4%、29.0%和70.6%。广州地方公共财政预算收入1141.79亿元,增长10.8%;如何做出下一年有效的财政收入预算,为下一年的政策提供指导依据,是一个具有重大意义的问题。
2、需求
要求:根据广州市1999年-2013年财政收入数据,预测广州市2014-2015年份的地方财政收入、增值税、营业税、企业所得税、个人所得税、政府性基金收入等数据。并给出相关建议。
3、分析思路
数据分析思路:
首先,阅读、理解以及整理收集到的数据,根据经济指标提炼数据,接着通过Adaptive_lasso方法进行特征选择,得到满足条件的特征变量;
其次,使用灰色预测对财政收入、增值税、营业税、企业所得税、个人所得税、政府性基金收入的影响因素2014-2015年数据进行预测,得到各影响因素2014-2015年数据。
再次,使用特征变量1999年-2015年数据,训练神经网络模型,再使用训练的模型预测2014-2015年广州市财政收入及各个类别收入数据;
最后,根据预测的数据,给广州财政局提出了几点合理的财政建议。
4、Adaptive-lasso指标筛选
Adaptive_lasso算法是近些年来被广泛应用于参数估计于变量选择的方法之一。Adaptive_Lasso算法能够解决最小二乘法和逐步回归局部最优解的不足,这是他的优点之一。Adaptive_lasso算法计算出某变量的特征值非零,则表示该变量对预测变量存在较大影响,而如果某变量的特征值为零,则表示该变量对预测变量影响很小。
4.1 地方财政收入影响元素指标筛选
1)指标初步筛选
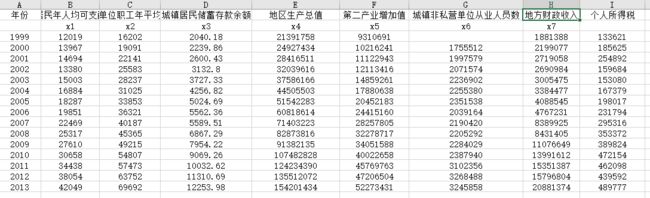
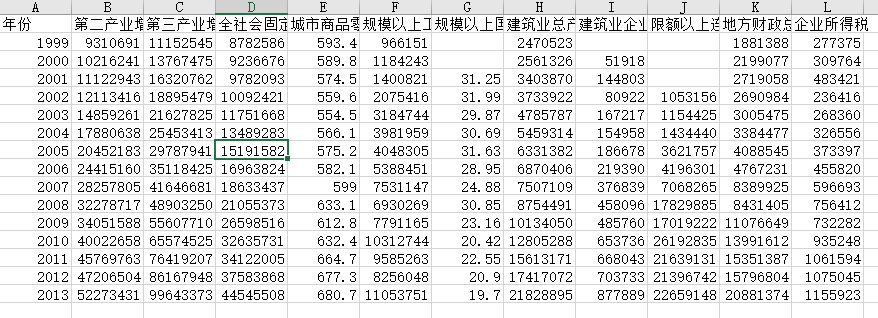
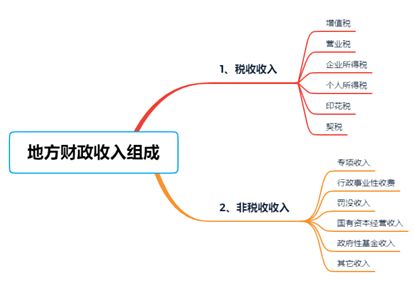
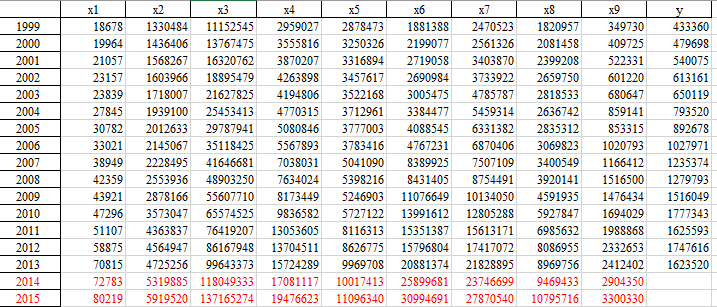
从1999年-2013年财政收入表数据中可以发现,地方财政收入组成主要包括:1、税收收入,主要包括企业所得税和地方所得税中中央和地方共享的40%,地方享有的25%的增值税、营业税、印花税等;2、非税收入,包括专项收入、行政事业性收费、罚没收入、国有资本经营收入和其他收入等。政府性基金收入是国家通过向社会征收以及出让土地、发行彩票等方式取得收入,并专项用于支持特定基础设施建设和社会事业发展的收入。地方财政收入组成如图7:
地方财政收入影响因素有很多,本文基于案例给予的数据,参考相关文献,以及对经济理论对财政收入的解释,最终我们初步确定了以下影响财政收入的因素:
X1城镇非私营单位从业人员数量:地区就业人数的上升,会引起地区人民收入总量的上升,从而间接影响财政收入的增加。
X2城镇单位职工年平均工资:城镇单位职工年平均工资能反映该地区的平均收入水平,并且职工收入增加,会引起地方财政的个人所得税总量的增加,从而影响财政收入的增加。
X3城镇人均可支配收入:城镇居民的可支配收入能反映他们的潜在消费能力,可支配收入越高,消费水平越高,从而会影响该地区的营业总额增加;而营业总额的增加,地方财政会获得更多的营业税收收入,从而促使财政收入的增长。
X4城镇居民储蓄存款余额:城镇居民储蓄存款余额能反映城镇居民的收入水平,储蓄水平高,收入也高,进而影响地方财政的个人税收收入。因此,城镇居民储蓄存在余额也是
影响财政收入的因素之一。
X5全社会固定资产投资额:是固定资产再生产活动,其内容包含建造和购置固定资产的经济活动。固定资产的投资能促进经济增长,扩大税源,进而拉动财政税收收入整体增长。
X6地区生产总值:表示地方经济发展水平。通常而言,政府财政收入来源于即期的地区生产总值。在国家经济政策不变、社会秩序稳定的情况下,地方经济发展水平与地方财政收入之间存在着密切的相关性,越是经济发达的地区,其财政收入的规模就越大。
X7第一产业增值:第一产业包括农业(包括种植业、林业、牧业和渔业)。广东市在2005年取消了农业税,因而第一产业对财政收入的影响会较小。
X8第三产业与第二产业产值比:表示产业结构。三个产业生产总值代表国民经济水平,而生产总值是财政收入的主要影响因素,当产业结构逐步优化时,财政收入也会随之增加。
X9总税收:税收收入往往是地方财政收入的主要来源之一,其具有征收的强制性、无偿性和固定性特点,可以为政府履行其职能提供充足的资金来源。因此,总税收的变化会极大的影响地方财政收入。
X10工业增值:工业产值增值一定程度上能反映该地区的生产总值的增值情况,而生产总值的增长是影响地方财政收入的主要因素之一。
2)pearson相关系数
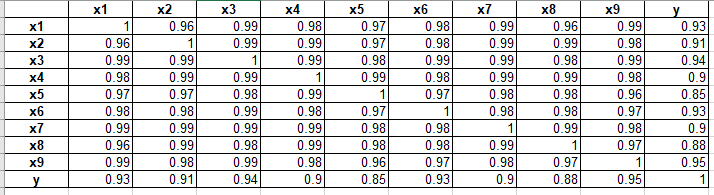
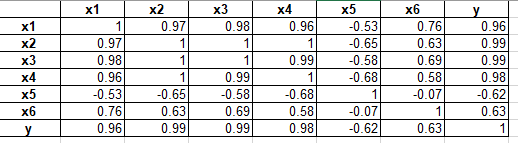
相关性分析主要用来检测目标变量与描述变量之间相关性分析,按照相关性可以分为正相关、负相关以及不相关,本文中的财政收入预测属于基于历史信息的线性正相关分析预测,因此,与财政收入相关的变量必须与其呈正相关关系,否则不采用该变量构建模型。财政收入与变量的Pearson相关性分析结果如表1所示:
从Pearson相关系数表中可以看出,本文选取的10个变量均与财政收入呈较高的正相关性,并且与财政收入呈显著相关性。因此,这些变量均满足要求,可以用于构建模型,进行预测。
3)lasso特征选择
本文选择Lasso算法解决Adaptive-lasso估计,确定特征变量。Lasso算法能够对变量进行筛选去重,可以将存在线性关系的变量进行去重。这也是本文选择该算法进行特征选择的原因之一。
特征选择结果如下:
从表3中可以看出,X2,X8的特征值结果为0,即这两个变量可能与其它变量存在共线关系,因而Adaptive-lasso将这两个变量剔除了。从实际角度考虑第一产业增值与第二/第三产业增值的比值很可能存在线性关系,城镇单位人均工资水平也与城镇居民人均可支配收入存在线性关系。特征选择的结果说明Adaptive-Lasso方法在构建模型时,能够剔除存在共线性关系的变量,同时体现了Adaptive-Lasso方法对多指标进行建模的优势。
4.2 营业税收入指标筛选
1)初步筛选
通过Adaptive-lasso算法确定的营业税影响因素。公路客运量(x1)、建筑业增加值(x2)、第三产业增加值(x3)、全社会房地产开发投资额(x4)、 全社会住宅投资额(x5)、地方财政收入(x6)、建筑业总产值(x7)、住宿和餐饮业零售额(x8)、限额以上餐饮业主营业务收入(x9)这些指标都可能与营业税收入存在关系。因此初步选择这些指标作为lasso输入变量。
2)pearson相关系数
对初步筛选的指标与营业税收入的相关性进行计算,结果如下表所示:
从营业税相关系数表看,影响营业税的各个数据指标都与营业税呈显著相关性,并且各个数据指标皆与营业税收入呈正相关。
3)lasso特征选择
将影响营业税收收入的x1-x9数据指标输入lasso特征选择,输出如下结果:
从上图特征选择结果看。x1-x9各个数据指标皆通过特征筛选。
4.3 增值税收入指标筛选
1)初步筛选
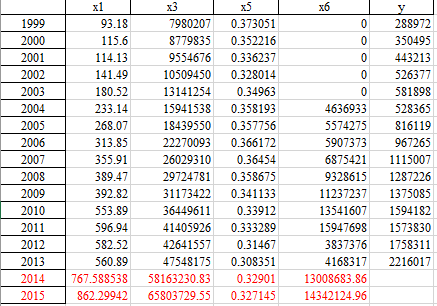
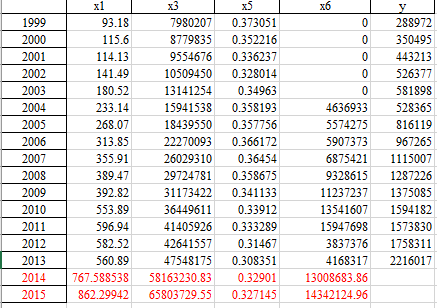
初步筛选出影响增值税的六个数据指标:商品进口总值(x1),地区生产总值(x2)、工业增加值(x3),批发零售业零售额(4)、工业增加值占GDP(x5)、批发零售业增加值(x6)。
2)pearson相关系数
对初步筛选的指标与增值税收入的相关性进行计算,结果如下表所示:
从山图中可以明显看出x1-x6这六个数据指标与增值税收入存在明显的线性关系,并且关系显著。并且除了x5与增值税收入呈负相关关系,其它皆与增值税收入呈正相关。
3)lasso特征选择
将x1-x6这个两个指标输入到lasso特征选择算法中,输出下表数据:
表中数据显示商品进口总值(x1),工业增加值(x3),工业增加值占GDP(x5)、批发零售业增加值(x6)这四个指标通过特征选择,而地区生产总值(x2)、批发零售业零售额(4)特征选择结果为0,因此被剔除。
4.4 企业所得税指标筛选
1)初步筛选
初步确定以下影响企业所得税收入的数据指标:第二产业增加值X1 、第三产业增加值X2 、全社会固定资产投资额X3 、 城市商品零售价格指数(1978=100)X4 、规模以上工业企业盈亏相抵后的利润总额X5 、 规模以上国有及国有控股工业企业企业亏损面X6 、建筑业总产值X7 、 建筑业企业利润总额X8、限额以上连锁店(公司)零售额X9 、地方财政总收入X10。
2)pearson相关系数
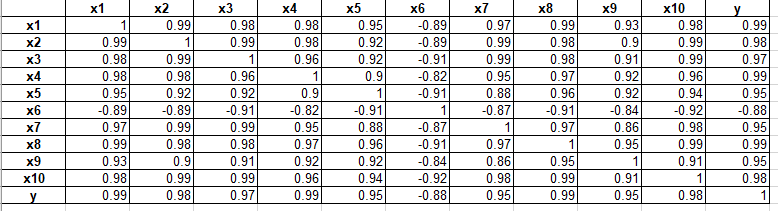
对初步筛选的指标与企业所得税收入的相关性进行计算,结果如下表所示:
上图数据显示,这10个数据指标与企业所得税相关都显著,除了规模以上国有及国有控股工业企业企业亏损面X6与企业所得税呈负相关,企业数据指标与企业所得税收入皆呈正相关。
3)lasso特征选择
将这9个数据指标输入到lasso特征选择算法中,输出如下结果:
从上图结果可以得出:第二产业增加值X1、全社会住宅投资额X4、规模以上工业企业盈亏相抵后的利润总额X5、规模以上国有及国有控股工业企业企业亏损面X6、限额以上连锁店(公司)零售额X9,这9个数据指标通过特征选择,其它数据指标皆被剔除。
4.5 个人所得税指标筛选
1)初步筛选
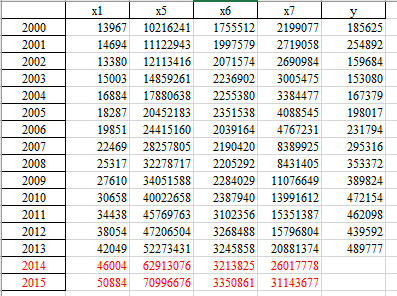
初步确定以下7个数据指标对个人所得税收入存在影响:城市居民年人均可支配收入x1、城镇单位职工年平均工资x2、城镇居民储蓄存款余额x3、地区生产总值x4、第二产业增加值x5、城镇非私营单位从业人员数x6、地方财政收入x7。
2)Pearson相关系数
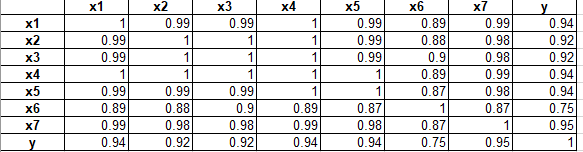
对初步筛选的指标与个人所得税收入的相关性进行计算,结果如下表所示:
上图结果显示,这7个数据指标与个人所得税存在显著相关性,并且都呈线性正相关关系。
3)lasso特征选择
将这7个数据指标输入到lasso特征选择算法中,输出如下结果:
由上图可以得到,个人所得税特征选择结果:城市居民年人均可支配收入X1、第二产业增加值X5、城镇非私营单位从业人员数X6、地方财政收入X7,这四个指标通过特征选择,其它指标特征选择结果为0 ,不满足条件。
5、灰色预测各项收入
灰色预测法是一种对含有不确定因素的系统进行预测的方法。灰色系统是介于白色系统和黑色系统之间的一种系统。白色系统是指一个系统的内部特征是完全已知的,即系统的信息是完全充分的。而黑色系统是指一个系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系来加以观测研究。灰色系统内的一部分信息是已知的,另一部分信息时未知的,系统内各因素间具有不确定的关系。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
本文通过灰色预测法预测影响因素2014-2015年值,灰色预测数据在用于神经网络模型训练。
灰色预测算法如下:
# -*- coding: utf-8 -*-
def GM11(x0): # 自定义灰色预测函数
import numpy as np
x1 = x0.cumsum() # 1-AGO序列
z1 = (x1[:len(x1) - 1] + x1[1:]) / 2.0 # 紧邻均值(MEAN)生成序列
z1 = z1.reshape((len(z1), 1))
B = np.append(-z1, np.ones_like(z1), axis=1)
Yn = x0[1:].reshape((len(x0) - 1, 1))
[[a], [b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) # 计算参数
f = lambda k: (x0[0] - b / a) * np.exp(-a * (k - 1)) - \
(x0[0] - b / a) * np.exp(-a * (k - 2)) # 还原值
delta = np.abs(x0 - np.array([f(i) for i in range(1, len(x0) + 1)]))
C = delta.std() / x0.std()
P = 1.0 * (np.abs(delta - delta.mean()) <0.6745 * x0.std()).sum() / len(x0)
return f, a, b, x0[0], C, P # 返回灰色预测函数、a、b、首项、方差比、小残差概率1)地方财政收入影响因素灰色预测
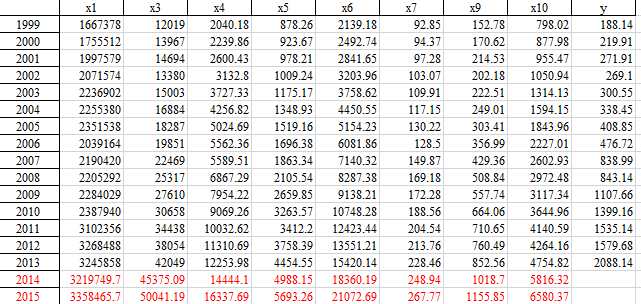
通过灰色预测算法预测地方财政收入影响因素2014-2015年数据,结果如下:
2)营业税影响因素灰色预测
通过灰色预测算法预测营业税收入影响因素2014-2015年数据,结果如下:
3)增值税影响因素灰色预测
通过灰色预测算法预测增值税收入影响因素2014-2015年数据,结果如下:
4)企业所得税影响因素灰色预测
通过灰色预测算法预测企业所得税收入影响因素2014-2015年数据,结果如下:
5)个人所得税影响因素灰色预测
通过灰色预测算法预测个人所得税收入影响因素2014-2015年数据,结果如下:
6、BP神经网络预测各项收入
在灰色预测法预测的数据基础上,本文通过python调用深度学习模块中的神经网络模型进行训练和学习。神经网络模型是一种深度学习算法,它在经过很多次训练学习后,进行预测分析具有很好的效果。并且由于神经网络有较强的适用性和容错能力,对历史数据建立训练模型,把灰色预测的数据带入训练好的模型中,就能得到充分考虑历史信息的预测结果,从而预测出2014-2015年广东市财政收入及各个类别的收入。
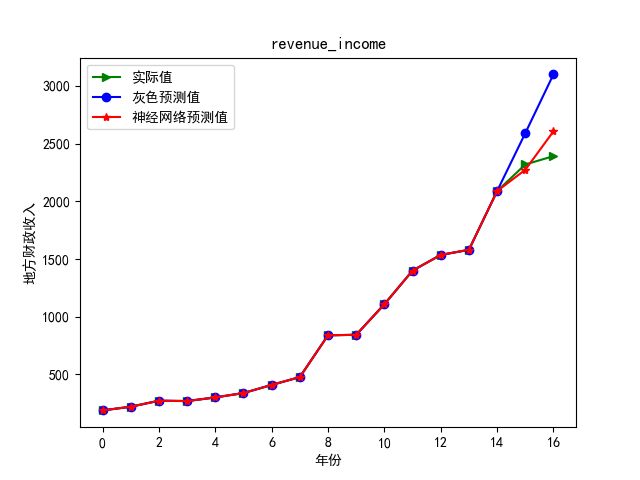
1)地方财政收入预测:
将灰色预测的数据导入已经构建好的神经网络模型中,进行训练。本文所构建的神经网络模型其参数设置为误差精度10-7,学习次数10000次,神经元个数为Lasso变量选择方法选择的变量个数8,隐藏层设置为12个节点。预测结果如下图所示:
2)营业税收入预测
将灰色预测的数据带入进神经网络中训练,模型参数设置为:误差精度10-7,学习次数10000次,输入层数9,隐藏层6个节点。营业税预测结果为:
3)增值税收入预测
将灰色预测的数据输入到神经网络模型中,并设置模型参数:输入层为4,隐藏层为6,误差精度10-7,学习次数10000次。
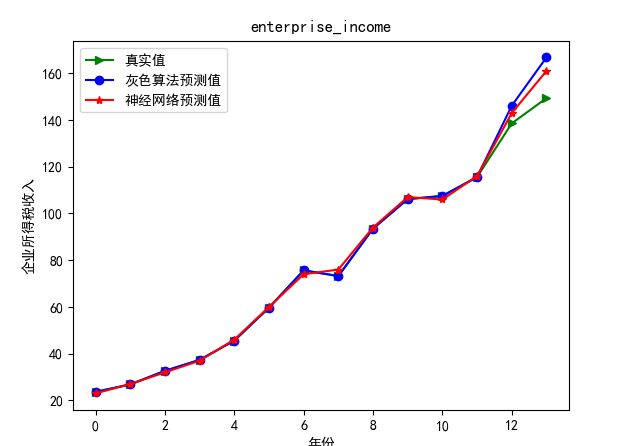
4)企业所得税预测
将灰色预测的变量数据导入已经构建好的神经网络模型中,模型参数设置为:输入层为5,隐藏层为6,误差精度10-7,学习次数10000次。得到如下结果:
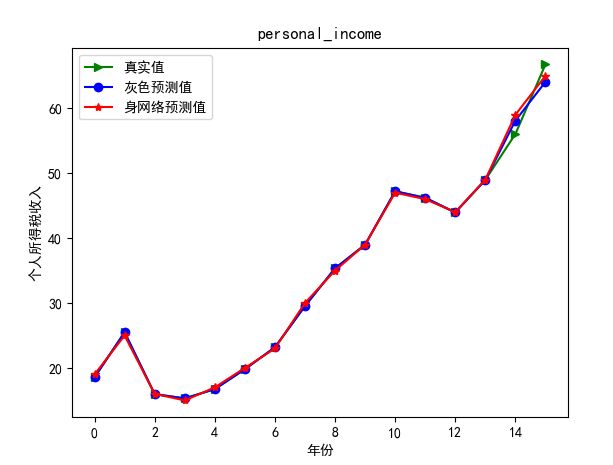
5)个人所得税预测
最后,将灰色预测数据导入神经网络模型中训练,模型参数设置为:输入层为4,隐藏层为6,误差精度10-7,学习次数15000次。得到如下结果:
7、建议
-------------
8、程序源码
# -*- coding :utf-8 -*-
#@max_xu
#2020.6.20
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from GM11 import GM11
#财政收入Lasso变量特征选择
def adaptiveLasso1():
#Adaptive-Lasso变量选择模型
inputfile = '原始数据\财政收入影响因素.xlsx '
data = pd.read_excel(inputfile)
# 导入AdaptiveLasso算法
from sklearn.linear_model import LassoLarsCV
model = LassoLarsCV()
x = data.iloc[:, 1:11] #选取1-16行,1-11列数据作为变量x1-x10
y = data['y'] #选取1-16行,10列数据作为变量y
model.fit(x,y)
print('财政收入Lasso 特征选择:\n',model.coef_)
#财政收入灰色预测
def huise1():
# 灰色预测,变量'x1','x2','x3','x4','x5','x6','x8','x9','x10'2014-2015年值
inputfile = '原始数据\财政收入影响因素.xlsx '
outputfile = '预测数据\财政收入灰色预测.xls'
data = pd.read_excel(inputfile)
data.index = range(1999, 2014) #读取2014年以前的财政收入表数据
data.loc[2014] = None
data.loc[2015] = None
l = ['x1','x3', 'x4', 'x5','x6','x7', 'x9','x10','y'] #实际测试出的特征序列
print('财政收入后验差值数据:')
for i in l:
f = GM11(data[i][:-2].values)[0] # 调用模型
C = GM11(data[i][np.arange(2000, 2014)].values)[4]
print(u' %s 后验差比值为:%0.4f' % (i, C))
data[i][2014] = f(len(data) - 1) # 2014年预测结果
data[i][2015] = f(len(data)) # 2015年预测结果
data[i] = data[i].round(2) # 保留2位小数
# data[l].to_excel(outputfile) # 结果输出
#财政收入神经网络模型
def revenue_predict():
# 神经网络模型构建
inputfile = r'预测数据\财政收入灰色预测.xls' # 灰色预测结果保存路径
outputfile = r'预测数据\revenue_predict.xls' # 结果输出路径
modelfile = r'预测数据\1-net.model' # 模型保存路径
data = pd.read_excel(inputfile) # 读取数据
feature = ['x1','x3', 'x4', 'x5','x6','x7', 'x9','x10'] #特征序列
data_train = data.loc[np.arange(1999, 2014) - 1999].copy() # 取2014年数据建模
# data_train = data.loc[np.arange(1999, 2014) - 1999].copy() #取2014年数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train_normal = (data_train - data_mean) / data_std # 数据标准化,按列索引(列名)计算
x_train = data_train_normal[feature].values # 特征数据
y_train = data_train_normal['y'].values # 标签数据
from keras.models import Sequential
from keras.layers.core import Dense, Activation
# 构建神经网络模型
model = Sequential() # 建立模型
model.add(Dense(input_dim=8, units=12))
model.add(Activation('relu')) # 用relu函数作为激活函数,能够大幅提供准确度
model.add(Dense(input_dim=12, units=1))
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型
model.fit(x_train, y_train, nb_epoch=10000, batch_size=16) # 训练模型,学习一万次
# model.save_weights(modelfile) # 保存模型参数
# 预测,并还原结果
x = ((data[feature] - data_mean[feature]) / data_std[feature]).values
data[u'y_pred'] = model.predict(x) * data_std['y'] + data_mean['y']
#保存数据
# data.to_excel(outputfile)
# 绘制预测结果图
import matplotlib as lib # 画出预测结果图
lib.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文
plt.figure('地方财政收入预测')
plt.xlabel('年份')
plt.ylabel('地方财政收入')
plt.title('revenue_income')
plt.plot(data['y_true'], 'g->', label='实际值') # 真实值数据
plt.plot( data['y'], 'b-o',label='灰色预测值') #灰色预测值
plt.plot(data['y_pred'], 'r-*',label='神经网络预测值') # 神经网络预测结果
plt.legend()
plt.show()
#增值税Lasso特征选择
def adaptiveLasso2():
# Adaptive-Lasso变量选择
inputfile = '原始数据\增值税影响因素.xlsx' # 输入的数据文件
data = pd.read_excel(inputfile) # 读取数据
from sklearn.linear_model import LassoLarsCV
model = LassoLarsCV()
x, y = data.iloc[5:, 1:7], data[5:]['y']
model.fit(x, y)
print('Lasso 特征选择:\n',model.coef_) # 各个特征的系数
#增值税灰色预测
def huise2():
inputfile = '原始数据\增值税影响因素.xlsx' # 输入的数据文件
outputfile = '预测数据\增值税灰色预测1.xls' # 灰色预测后保存的路径
data = pd.read_excel(inputfile) # 读取数据
data.index = range(1999, 2014)
data.loc[2014] = None
data.loc[2015] = None
l = ['x1','x3','x5','x6','y'] #实际测试出的特征序列
print('增值税后验差值数据:')
for i in l:
f = GM11(data[i][np.arange(1999, 2014)].values)[0]
C = GM11(data[i][np.arange(2000, 2014)].values)[4]
print(u' %s 后验差比值为:%0.4f' % (i, C))
data[i][2014] = f(len(data) - 1) # 2014年预测结果
data[i][2015] = f(len(data)) # 2015年预测结果
data[i] = data[i].round(6) # 保留六位小数
data[l].to_excel(outputfile) # 结果输出
# print(data)
#增值税神经网络预测
def increase_tax_predict():
#增值税神经网络预测模型
inputfile = '预测数据\增值税灰色预测.xls' # 灰色预测后保存的路径
outputfile = '预测数据\increase_predict.xls' # 神经网络预测后保存的结果
modelfile = '预测数据/2-net.model' # 模型保存路径
data = pd.read_excel(inputfile) # 读取数据
feature = ['x1','x3','x5','x6'] # 特征所在列
data_train = data.loc[np.arange(1999, 2014) - 1999].copy() # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean) / data_std # 数据标准化
x_train = data_train[feature].values # 特征数据
y_train = data_train['y'].values # 标签数据
from keras.models import Sequential
from keras.layers.core import Dense, Activation
model = Sequential() # 建立模型
model.add(Dense(input_dim=4, units=6))
model.add(Activation('relu')) # 用relu函数作为激活函数,能够大幅提供准确度
model.add(Dense(input_dim=6, units=1))
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型
model.fit(x_train, y_train, nb_epoch=10000, batch_size=16) # 训练模型,学习一万次
# model.save_weights(modelfile) # 保存模型参数
# 预测,并还原结果。
x = ((data[feature] - data_mean[feature]) / data_std[feature]).values
data[u'y_pred'] = model.predict(x) * data_std['y'] + data_mean['y']
data[u'y_pred'] = data[u'y_pred'].round(2)
# data.to_excel(outputfile)
import matplotlib.pyplot as plt # 画出预测结果图
# 绘制预测结果图
import matplotlib as lib # 画出预测结果图
lib.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文
plt.figure('增值税收入预测')
plt.xlabel('年份')
plt.ylabel('增值税收入')
plt.title('increase_predict')
plt.plot(data['y_true'], 'g->',label = '真实值') #真实收入
plt.plot(data['y'], 'b-o',label = '灰色预测值') #灰色预测值
plt.plot(data['y_pred'], 'r-*',label = '神经网络预测值') # 神经网络预测结果
plt.legend()
plt.show()
#营业税Lasso变量特征选择
def adaptiveLasso3():
# Adaptive-Lasso变量选择
inputfile = '原始数据\营业税影响因素.xlsx' # 输入的数据文件
data = pd.read_excel(inputfile) # 读取数据
# 导入AdaptiveLasso算法
from sklearn.linear_model import LassoLarsCV
model = LassoLarsCV()
x,y = data.iloc[:, 0:9], data['y']
model.fit(x,y)
print('Lasso 特征选择:\n', model.coef_) # 各个特征的系数
# 营业税灰色预测
def huise3():
inputfile = '原始数据\营业税影响因素.xlsx' # 输入的数据文件
outputfile = '预测数据\营业税灰色预测.xls' # 灰色预测后保存的路径
data = pd.read_excel(inputfile) # 读取数据
data.index = range(1999, 2014)
data.loc[2014] = None
data.loc[2015] = None
l = ['x1','x2','x3','x4','x5','x6','x7','x8','x9','y']#实际测试出的特征序列
print('营业税后验差值数据:')
for i in l:
f = GM11(data[i][np.arange(1999, 2014)].values)[0]
C = GM11(data[i][np.arange(2000, 2014)].values)[4]
print(u' %s 后验差比值为:%0.4f' % (i, C))
data[i][2014] = f(len(data) - 1) # 2014年预测结果
data[i][2015] = f(len(data)) # 2015年预测结果
data[i] = data[i].round() # 取整
# data[l ].to_excel(outputfile) # 结果输出
# print(data)
# 营业税神经网络模型
def sale_tax_predict():
inputfile = r'预测数据\营业税灰色预测.xls' # 灰色预测后保存的路径
outputfile = r'预测数据\sales_tax.xls' # 神经网络预测后保存的结果
modelfile = r'预测数据\3-net.model' # 模型保存路径
data = pd.read_excel(inputfile) # 读取数据
feature = ['x1','x2','x3','x4','x5','x6','x7','x8','x9']
data_train = data.loc[np.arange(1999, 2014)-1999].copy() # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean) / data_std # 数据标准化
x_train = data_train[feature].values # 特征数据
y_train = data_train['y'].values # 标签数据
from keras.models import Sequential
from keras.layers.core import Dense, Activation
model = Sequential() # 建立模型
model.add(Dense(input_dim=9, units=6))
model.add(Activation('relu')) # 用relu函数作为激活函数,能够大幅提供准确度
model.add(Dense(input_dim=6, units=1))
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型
model.fit(x_train, y_train, nb_epoch=10000, batch_size=16) # 训练模型,学习一万次
# model.save_weights(modelfile) # 保存模型参数
# 预测,并还原结果。
x = ((data[feature] - data_mean[feature]) / data_std[feature]).values
data[u'y_pred'] = model.predict(x) * data_std['y'] + data_mean['y']
data[u'y_pred'] = data[u'y_pred'].round(2)
# data.to_excel(outputfile)
import matplotlib.pyplot as plt # 画出预测结果图
# 绘制预测结果图
# 绘制预测结果图
import matplotlib as lib # 画出预测结果图
lib.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文
plt.figure('营业税收入预测')
plt.xlabel('年份')
plt.ylabel('营业税收入')
plt.title('sales_tax')
plt.plot(data['y_true'], 'g->', label='真实值') #真实值
plt.plot(data['y'], 'b-o',label = '灰色预测值' ) # 灰色预测结果
plt.plot(data['y_pred'], 'r-*',label = '神经网络预测值') # 神经网络预测结果
plt.legend()
plt.show()
#企业所得税特征选择
def adaptiveLasso4():
inputfile = '原始数据\企业所得税影响因素.xlsx' # 输入的数据文件
data = pd.read_excel(inputfile) # 读取数据
# 导入AdaptiveLasso算法,要在较新的Scikit-Learn才有。
from sklearn.linear_model import LassoCV
from sklearn.linear_model import LassoLarsCV
model = LassoLarsCV()
model.fit(data.iloc[:, 0:10], data['y'])
print('Lasso 特征选择:\n', model.coef_) # 各个特征的系数
#企业所得税灰色预测
def huise4():
inputfile = '原始数据\企业所得税影响因素.xlsx' # 输入的数据文件
outputfile = '预测数据\企业所得税灰色预测.xls' # 灰色预测后保存的路径
data = pd.read_excel(inputfile) # 读取数据
data.index = range(2002, 2014)
data.loc[2014] = None
data.loc[2015] = None
l = ['x1', 'x2', 'x9','y' ]#实际测试出的特征序列
print('企业所得税后验差值数据:')
for i in l:
f = GM11(data[i][np.arange(2002, 2014)].values)[0]
C = GM11(data[i][np.arange(2002, 2014)].values)[4]
print(u' %s 后验差比值为:%0.4f' % (i, C))
data[i][2014] = f(len(data) - 1) # 2014年预测结果
data[i][2015] = f(len(data)) # 2015年预测结果
data[i] = data[i].round(2) # 保留两位小数
data[l].to_excel(outputfile) # 结果输出
# print(data)
#企业所得税神经网络预测模型
def enterprise_income_predict():
inputfile = '预测数据\企业所得税灰色预测.xls' # 灰色预测后保存的路径
outputfile = '预测数据/enterprise_income.xls' # 神经网络预测后保存的结果
modelfile = '预测数据/4-net.model' # 模型保存路径
data = pd.read_excel(inputfile) # 读取数据
feature = ['x1', 'x2', 'x9'] # 特征所在列
data_train = data.loc[np.arange(2002, 2014)-2002].copy() # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean) / data_std # 数据标准化
x_train = data_train[feature].values # 特征数据
y_train = data_train['y'].values # 标签数据
from keras.models import Sequential
from keras.layers.core import Dense, Activation
model = Sequential() # 建立模型
model.add(Dense(input_dim=3, units=6))
model.add(Activation('relu')) # 用relu函数作为激活函数,能够大幅提供准确度
model.add(Dense(input_dim=6, units=1))
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型
model.fit(x_train, y_train, nb_epoch=10000, batch_size=16) # 训练模型,学习五千次
# model.save_weights(modelfile) # 保存模型参数
# 预测,并还原结果。
x = ((data[feature] - data_mean[feature]) / data_std[feature]).values
data[u'y_pred'] = model.predict(x) * data_std['y'] + data_mean['y']
data[u'y_pred'] = data[u'y_pred'].round()
data.to_excel(outputfile)
import matplotlib.pyplot as plt # 画出预测结果图
# 绘制预测结果图
import matplotlib as lib # 画出预测结果图
lib.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文
plt.figure('企业所得税收入预测')
plt.xlabel('年份')
plt.ylabel('企业所得税收入')
plt.title('enterprise_income')
plt.plot(data['y_true'], 'g->',label = '真实值') #真实值
plt.plot(data['y'], 'b-o',label = '灰色算法预测值') #灰色算法预测值
plt.plot(data['y_pred'], 'r-*',label = '神经网络预测值') # 神经网络预测结果
plt.legend()
plt.show()
#个所得税 Adaptive-Lasso变量选择
def adaptiveLasso5():
inputfile = '原始数据\个人所得税影响因素.xlsx' # 输入的数据文件
data = pd.read_excel(inputfile) # 读取数据
# 导入AdaptiveLasso算法,要在较新的Scikit-Learn才有。
from sklearn.linear_model import LassoLarsCV
model = LassoLarsCV()
model.fit(data.iloc[:, 1:8], data['y'])
print('Lasso 特征选择:\n',model.coef_) # 各个特征的系数
#个人所得税灰色预测
def huise5():
inputfile = r'原始数据\个人所得税影响因素.xlsx' # 输入的数据文件
outputfile = r'预测数据\个人所得税灰色预测.xls' # 灰色预测后保存的路径
data = pd.read_excel(inputfile) # 读取数据
data.index = range(2000, 2014)
data.loc[2014] = None
data.loc[2015] = None
l = ['x1' ,'x5','x6', 'x7','y']#实际测试出的特征序列
print('个人所得税后验差值数据:')
for i in l:
f = GM11(data[i][np.arange(2000, 2014)].values)[0]
C = GM11(data[i][np.arange(2000, 2014)].values)[4]
print(u' %s 后验差比值为:%0.4f' %(i, C))
data[i][2014] = f(len(data) - 1) # 2014年预测结果
data[i][2015] = f(len(data)) # 2015年预测结果
data[i] = data[i].round() # 取整
# data[l].to_excel(outputfile) # 结果输出
# print(data)
# 个人所得税神经网络预测模型
def personal_income_predict():
inputfile = r'预测数据\个人所得税灰色预测.xls' # 灰色预测后保存的路径
outputfile = r'预测数据\personal_income.xls' # 神经网络预测后保存的结果
modelfile = r'预测数据\5-net.model' # 模型保存路径
data = pd.read_excel(inputfile) # 读取数据
feature = ['x1' ,'x5','x6', 'x7'] # 特征所在列
# feature = ['x1', 'x4', 'x5', 'x7']
data_train = data.loc[np.arange(2000, 2014)-2000].copy() # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean) / data_std # 数据标准化
x_train = data_train[feature].values # 特征数据
y_train = data_train['y'].values # 标签数据
from keras.models import Sequential
from keras.layers.core import Dense, Activation
model = Sequential() # 建立模型
model.add(Dense(input_dim=4, units=8))
model.add(Activation('relu')) # 用relu函数作为激活函数,能够大幅提供准确度
model.add(Dense(input_dim=8, units=1))
model.compile(loss='mean_squared_error', optimizer='adam') # 编译模型
model.fit(x_train, y_train, nb_epoch=15000, batch_size=16) # 训练模型,学习一万五千次
# model.save_weights(modelfile) # 保存模型参数
# 预测,并还原结果。
x = ((data[feature] - data_mean[feature]) / data_std[feature]).values
data[u'y_pred'] = model.predict(x) * data_std['y'] + data_mean['y']
data[u'y_pred'] = data[u'y_pred'].round()
# data.to_excel(outputfile)
import matplotlib.pyplot as plt # 画出预测结果图
# 绘制预测结果图
# 绘制预测结果图
import matplotlib as lib # 画出预测结果图
lib.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文
plt.figure('个人所得税收入预测')
plt.xlabel('年份')
plt.ylabel('个人所得税收入')
plt.title('personal_income')
plt.plot(data['y_true'], 'g->',label = '真实值') #真实值
plt.plot(data['y'], 'b-o',label = '灰色预测值') #灰色预测值
plt.plot(data['y_pred'], 'r-*',label = '身网络预测值') # 神经网络预测结果
plt.legend()
plt.show()
# 政府性基金收入灰色预测
def huise6():
data = pd.read_excel('预测数据\模型预测结果\政府性基金收入.xlsx')
outputfile = '预测数据\政府性基金收入灰色预测.xls'
data.index = range(2007, 2014)
data.loc[2014] = None
data.loc[2015] = None
print(data)
f = GM11(data['x1'][np.arange(2007, 2014)].values)[0]
C = GM11(data['x1'][np.arange(2007, 2014)].values)[4]
print(u'2014年、2015年的预测结果分别为:\n %0.2f万元和%0.2f万元' % (f(8), f(9)))
print(u'后验差比值为:%0.4f' % C)
data['x1'][2014] = (f(8)-1)
data['x1'][2015] = f(len(data)) # 预测每年结果
data['x1'] = data['x1'].round(3) # 取整
print(data)
# data.to_excel(outputfile)
#导入数据包
import matplotlib as lib
inputfile = r'预测数据\政府性基金收入灰色预测.xls'
data = pd.read_excel(inputfile)
lib.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文
plt.figure('政府性基金灰色预测')
plt.xlabel('年份')
plt.ylabel('政府性基金收入')
plt.title('政府性基金收入')
plt.plot(data['Date'], data['x1'], 'b-o', label='预测值')
# 神经网络预测结果
plt.legend()
plt.show()
if __name__ == '__main__':
# 1、财政收入预测
adaptiveLasso1()
huise1()
revenue_predict()
##2、增值税预测
# adaptiveLasso2()
# huise2()
# increase_tax_predict()
#3、营业税预测
# adaptiveLasso3()
# huise3()
# sale_tax_predict()
##4、企业所得税预测
# adaptiveLasso4()
# huise4()
# enterprise_income_predict()
##5、个人所得税预测
# adaptiveLasso5()
# huise5()
# personal_income_predict()
##6、政府性基金收入
# huise6()