深度学习与PyTorch笔记16
2D函数优化实例
Himmelblau function(专门检测优化器效果的函数)
f ( x , y ) = ( x 2 + y − 11 ) 2 + ( x + y 2 − 7 ) 2 f(x,y)=(x^{2}+y-11)^{2}+(x+y^{2}-7)^{2} f(x,y)=(x2+y−11)2+(x+y2−7)2
四个局部最小值的解都为0,局部最小即位全局最小。
f ( 3.0 , 2.0 ) = 0.0 f(3.0,2.0)=0.0 f(3.0,2.0)=0.0
f ( − 2.805118 , 3.131312 ) = 0.0 f(-2.805118,3.131312)=0.0 f(−2.805118,3.131312)=0.0
f ( − 3.779310 , − 3.283186 ) = 0.0 f(-3.779310,-3.283186)=0.0 f(−3.779310,−3.283186)=0.0
f ( 3.584428 , − 1.848126 ) = 0.0 f(3.584428,-1.848126)=0.0 f(3.584428,−1.848126)=0.0
通过比较解来验证优化器好不好。
np.meshgrid()
传入参数后,生成相应图片,每张图片相同位置上的点拼在一起形成坐标。
optimizer = torch.optim.Adam([x], lr=1e-3)
第一个参数为优化目标,第二个参数为学习率。只要得到梯度,此函数就可以完成 x ′ = x − 0.001 ∇ x x^{'}=x-0.001\nabla_{x} x′=x−0.001∇x, y ′ = y − 0.001 ∇ y y^{'}=y-0.001\nabla_{y} y′=y−0.001∇y的操作,每调用一次optimizer.step()就更新一次这个过程。
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import torch
#定义函数
def himmelblau(x):
return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2
#将函数可视化
#生成x轴从-6到6,y轴从-6到6的矩阵
x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
X, Y = np.meshgrid(x, y)#生成坐标
print('X,Y maps:', X.shape, Y.shape)
Z = himmelblau([X, Y])#将x,y坐标传入函数得到Z的坐标
fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
#可尝试多个初始化的值 [1., 0.], [-4, 0.], [4, 0.],此处优化的是pred,优化目标是x
x = torch.tensor([0., 0.], requires_grad=True)#设置梯度信息
optimizer = torch.optim.Adam([x], lr=1e-3)#使用优化器
for step in range(20000):
pred = himmelblau(x)#送进初始值,得到一个预测值
optimizer.zero_grad()#梯度清零
pred.backward()#直接调用预测值,生成关于x,y的梯度信息
optimizer.step()#更新
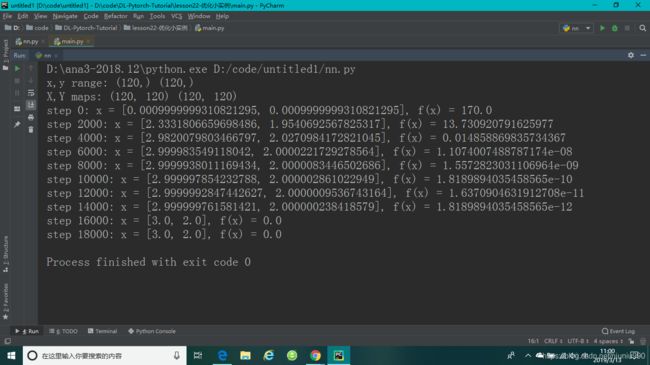
if step % 2000 == 0:
print ('step {}: x = {}, f(x) = {}'
.format(step, x.tolist(), pred.item()))