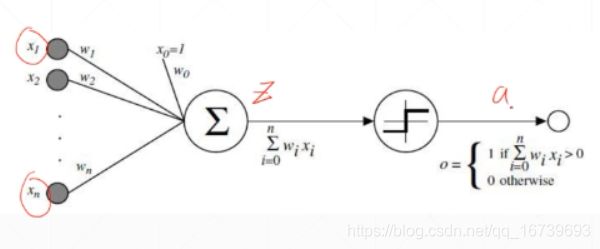
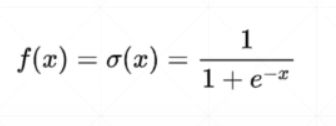【PyTorch学习笔记】7:激活函数,损失函数,使用PyTorch求导
激活函数
在PyTorch的老版本里这些激活函数在torch.nn.functional下,现在大多已经改到了torch下。
Sigmoid
import torch
a = torch.linspace(-100, 100, 10)
print(torch.sigmoid(a))
运行结果:
tensor([0.0000e+00, 1.6655e-34, 7.4564e-25, 3.3382e-15, 1.4945e-05, 9.9999e-01,
1.0000e+00, 1.0000e+00, 1.0000e+00, 1.0000e+00])
当x趋近与无穷大或者无穷小时,函数的梯度趋近于0,梯度长时间得不到更新,长时间Loss保持不变,造成梯度弥散
Tanh
b = torch.linspace(-1, 1, 10)
print(torch.tanh(b))
运行结果:
tensor([-0.7616, -0.6514, -0.5047, -0.3215, -0.1107, 0.1107, 0.3215, 0.5047,
0.6514, 0.7616])
ReLU
即Rectified Linear Unit,是现在DL用得最多的激活函数。ReLU在输入正信号时保证输出信号的导数是1,避免了当输入过大时引起(前面Sigmoid或者Tanh都会出现的)梯度弥散。
c = torch.linspace(-1, 1, 10)
print(torch.relu_(c))
运行结果:
tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1111, 0.3333, 0.5556, 0.7778,
1.0000])
Softmax
可以用于将多个输出转换成多个概率值,使每个值都符合概率的定义(在0到1),且概率相加和为1,非常适合多分类问题。Softmax往往用在最后对输出值y的处理上。它会将原来大的值相对缩放得更大,而原来很小的值压缩到比较密集的空间(这从指数函数图像就可以理解)
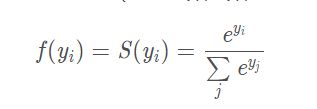
import torch
from torch.nn import functional as F
y = torch.rand(3, requires_grad=True)
print(y)
# 因为进行Softmax操作涉及到组内的其它结点的值,所以要特别注意dim的设置
p = F.softmax(y, dim=0)
print(p)
运行结果:
tensor([0.7440, 0.1704, 0.7994], requires_grad=True)
tensor([0.3816, 0.2150, 0.4034], grad_fn=<SoftmaxBackward>)
注意,因为Softmax涉及其它结点的值的信息,每个结点 y k y_k yk经Softmax得到结点 p k p_k pk,计算导数时也要计算对其它结点的偏导(i不等于j的情况)
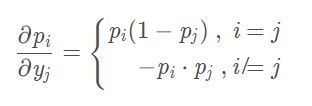
这里也能看出,当i=j时得到的导数值为正,也就是 y k y_k yk 越大,自然得到的概率 p k p_k pk 也就应该越大;而当i≠j时得到的导数值为负,因为 y i y_i yi越大,肯定要让得到其它类别的概率 p i p_i pi越小,这是符合对多分类的概率的直观感受的。
# 注意计算导数时,LOSS只能是一个值的,不能是有多个分量的
# 但是可以对多个东西去求偏导
# 计算p1对y0,y1,y2的导数
print(torch.autograd.grad(p[1], [y], retain_graph=True))
# 计算p2对y0,y1,y2的导数
print(torch.autograd.grad(p[2], [y]))
运行结果:
(tensor([-0.0821, 0.1688, -0.0867]),)
(tensor([-0.1539, -0.0867, 0.2407]),)
损失函数
这些LOSS都定义在torch.nn.functional下,可以直接使用。
Mean Squared Error
MSE即均方误差,常用在数值型输出上。
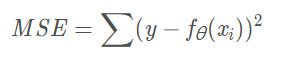
其中θ是网络的参数,取决于使用的网络结构,例如如果只是普通的线性感知器,那么:
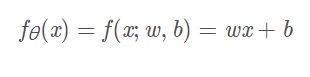
注意MSE和L2范数相比,L2范数是做了开平方操作的,所以如果要使用它来求MSE,最后只要.pow(2)平方一下就可以了。
tensor([0.7440, 0.1704, 0.7994], requires_grad=True)
tensor([0.3816, 0.2150, 0.4034], grad_fn=<SoftmaxBackward>)
更多看原博文:
https://blog.csdn.net/SHU15121856/article/details/88696520