PCL ——最小包围盒

1.包围盒简介

  包围盒也叫外接最小矩形,是一种求解离散点集最优包围空间的算法，基本思想是用体积稍大且特性简单的几何体（称为包围盒）来近似地代替复杂的几何对象。
  常见的包围盒算法有AABB包围盒、包围球、方向包围盒OBB以及固定方向凸包FDH。碰撞检测问题在虚拟现实、计算机辅助设计与制造、游戏及机器人等领域有着广泛的应用，甚至成为关键技术。而包围盒算法是进行碰撞干涉初步检测的重要方法之一。

  在此借助于PCL点云库寻找点云的最小包围盒,代码参考网上代码,因为工程需要包围盒的顶点坐标或偏转角度,网上代码都只画出了最小包围盒没有求出顶点坐标,所以自己折腾了很久终于把顶点坐标求出,下面将代码放出来供大家参考.

---

2.原理简述

最小包围盒的计算过程大致如下:
1.利用PCA主元分析法获得点云的三个主方向，获取质心，计算协方差，获得协方差矩阵，求取协方差矩阵的特征值和特长向量，特征向量即为主方向。
2.利用1中获得的主方向和质心，将输入点云转换至原点，且主方向与坐标系方向重回，建立变换到原点的点云的包围盒。
3.给输入点云设置主方向和包围盒，通过输入点云到原点点云变换的逆变换实现。

---

最小包围盒顶点计算的过程大致如下:
1.输入点云转换至远点后,求得变换后点云的最大最小x,y,z轴的坐标,此时(max.x,max.y,max.z),(max.x,min.y,max.z),(max.x,max.y,min.z),(min.x,max.y,max.z),(min.x,max.y,min.z),(min.x,min.y,max.z),(min.x,min.y,max.z),(min.x,min.y,min.z)
即为变换后点云的包围盒,也是原始输入点云包围盒顶点坐标经过变化后的坐标.
2.将上述求得的6个包围盒坐标逆变换回输入点云的坐标系,即得到原始输入点云的包围盒顶点坐标.

---

3.详细代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 


using namespace std;
typedef pcl::PointXYZ PointType;
typedef struct myPointType  
{  
    double x;  //mm world coordinate x  
    double y;  //mm world coordinate y  
    double z;  //mm world coordinate z  
	int num;   //point num
}; 

// Get N bits of the string from back to front.
char* Substrend(char*str,int n)
{
	char *substr=(char*)malloc(n+1);
	int length=strlen(str);
	if (n>=length)
	{
		strcpy(substr,str);
		return substr;
	}
	int k=0;
	for (int i=length-n;i<length;i++)
	{
		substr[k]=str[i];
		k++;
	}
	substr[k]='\0';
	return substr;
}

int main(int argc, char **argv)
{
	// create point cloud  
	pcl::PointCloud<PointType>::Ptr cloud(new pcl::PointCloud<PointType>());

	// load data
	char* fileType;
	if (argc>1)
	{
		fileType = Substrend(argv[1],3);
	}
	if (!strcmp(fileType,"pcd"))
	{
    	// load pcd file
		pcl::io::loadPCDFile(argv[1], *cloud);
	}
	else if(!strcmp(fileType,"txt"))
	{
		// load txt data file	
		int number_Txt;
		myPointType txtPoint; 
		vector<myPointType> points; 
		FILE *fp_txt; 
		fp_txt = fopen(argv[1], "r");  
		if (fp_txt)  
		{  
		    while (fscanf(fp_txt, "%lf %lf %lf", &txtPoint.x, &txtPoint.y, &txtPoint.z) != EOF)  
		    {  
		        points.push_back(txtPoint);  
		    }  
		}  
		else  
		    std::cout << "txt数据加载失败！" << endl;  
		number_Txt = points.size();  

		cloud->width = number_Txt;  
		cloud->height = 1;     
		cloud->is_dense = false;  
		cloud->points.resize(cloud->width * cloud->height);  
	  
		for (size_t i = 0; i < cloud->points.size(); ++i)  
		{  
		    cloud->points[i].x = points[i].x;  
		    cloud->points[i].y = points[i].y;  
		    cloud->points[i].z = 0;  
		}  
	}
	else 
	{
		std::cout << "please input data file name"<<endl;
		return 0;
	}

	// start calculating time
    pcl::StopWatch time;

	
    Eigen::Vector4f pcaCentroid;
    pcl::compute3DCentroid(*cloud, pcaCentroid);
    Eigen::Matrix3f covariance;
    pcl::computeCovarianceMatrixNormalized(*cloud, pcaCentroid, covariance);
    Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> eigen_solver(covariance, Eigen::ComputeEigenvectors);
    Eigen::Matrix3f eigenVectorsPCA = eigen_solver.eigenvectors();
    Eigen::Vector3f eigenValuesPCA = eigen_solver.eigenvalues();
    eigenVectorsPCA.col(2) = eigenVectorsPCA.col(0).cross(eigenVectorsPCA.col(1)); //校正主方向间垂直
    eigenVectorsPCA.col(0) = eigenVectorsPCA.col(1).cross(eigenVectorsPCA.col(2));
    eigenVectorsPCA.col(1) = eigenVectorsPCA.col(2).cross(eigenVectorsPCA.col(0));

    std::cout << "特征值va(3x1):\n" << eigenValuesPCA << std::endl;
    std::cout << "特征向量ve(3x3):\n" << eigenVectorsPCA << std::endl;
    std::cout << "质心点(4x1):\n" << pcaCentroid << std::endl;
    /*
    // 另一种计算点云协方差矩阵特征值和特征向量的方式:通过pcl中的pca接口，如下，这种情况得到的特征向量相似特征向量
    pcl::PointCloud::Ptr cloudPCAprojection (new pcl::PointCloud);
    pcl::PCA pca;
    pca.setInputCloud(cloudSegmented);
    pca.project(*cloudSegmented, *cloudPCAprojection);
    std::cerr << std::endl << "EigenVectors: " << pca.getEigenVectors() << std::endl;//计算特征向量
    std::cerr << std::endl << "EigenValues: " << pca.getEigenValues() << std::endl;//计算特征值
    */
    Eigen::Matrix4f tm = Eigen::Matrix4f::Identity();
    Eigen::Matrix4f tm_inv = Eigen::Matrix4f::Identity();
    tm.block<3, 3>(0, 0) = eigenVectorsPCA.transpose();   //R.
    tm.block<3, 1>(0, 3) = -1.0f * (eigenVectorsPCA.transpose()) *(pcaCentroid.head<3>());//  -R*t
    tm_inv = tm.inverse();

    std::cout << "变换矩阵tm(4x4):\n" << tm << std::endl;
    std::cout << "逆变矩阵tm'(4x4):\n" << tm_inv << std::endl;

    pcl::PointCloud<PointType>::Ptr transformedCloud(new pcl::PointCloud<PointType>);
    pcl::transformPointCloud(*cloud, *transformedCloud, tm);

    PointType min_p1, max_p1;
    Eigen::Vector3f c1, c;
    pcl::getMinMax3D(*transformedCloud, min_p1, max_p1);
    c1 = 0.5f*(min_p1.getVector3fMap() + max_p1.getVector3fMap());

    std::cout << "型心c1(3x1):\n" << c1 << std::endl;

    Eigen::Affine3f tm_inv_aff(tm_inv);
    pcl::transformPoint(c1, c, tm_inv_aff);

    Eigen::Vector3f whd, whd1;
    whd1 = max_p1.getVector3fMap() - min_p1.getVector3fMap();
    whd = whd1;
    float sc1 = (whd1(0) + whd1(1) + whd1(2)) / 3;  //点云平均尺度，用于设置主方向箭头大小

    std::cout << "width1=" << whd1(0) << endl;
    std::cout << "heght1=" << whd1(1) << endl;
    std::cout << "depth1=" << whd1(2) << endl;
    std::cout << "scale1=" << sc1 << endl;

    const Eigen::Quaternionf bboxQ1(Eigen::Quaternionf::Identity());
    const Eigen::Vector3f    bboxT1(c1);
    const Eigen::Quaternionf bboxQ(tm_inv.block<3, 3>(0, 0));
    const Eigen::Vector3f    bboxT(c);

    //变换到原点的点云主方向
    PointType op;
    op.x = 0.0;
    op.y = 0.0;
    op.z = 0.0;
    Eigen::Vector3f px, py, pz;
    Eigen::Affine3f tm_aff(tm);
    pcl::transformVector(eigenVectorsPCA.col(0), px, tm_aff);
    pcl::transformVector(eigenVectorsPCA.col(1), py, tm_aff);
    pcl::transformVector(eigenVectorsPCA.col(2), pz, tm_aff);
    PointType pcaX;
    pcaX.x = sc1 * px(0);
    pcaX.y = sc1 * px(1);
    pcaX.z = sc1 * px(2);
    PointType pcaY;
    pcaY.x = sc1 * py(0);
    pcaY.y = sc1 * py(1);
    pcaY.z = sc1 * py(2);
    PointType pcaZ;
    pcaZ.x = sc1 * pz(0);
    pcaZ.y = sc1 * pz(1);
    pcaZ.z = sc1 * pz(2);

    //初始点云的主方向
    PointType cp;
    cp.x = pcaCentroid(0);
    cp.y = pcaCentroid(1);
    cp.z = pcaCentroid(2);
    PointType pcX;
    pcX.x = sc1 * eigenVectorsPCA(0, 0) + cp.x;
    pcX.y = sc1 * eigenVectorsPCA(1, 0) + cp.y;
    pcX.z = sc1 * eigenVectorsPCA(2, 0) + cp.z;
    PointType pcY;
    pcY.x = sc1 * eigenVectorsPCA(0, 1) + cp.x;
    pcY.y = sc1 * eigenVectorsPCA(1, 1) + cp.y;
    pcY.z = sc1 * eigenVectorsPCA(2, 1) + cp.z;
    PointType pcZ;
    pcZ.x = sc1 * eigenVectorsPCA(0, 2) + cp.x;
    pcZ.y = sc1 * eigenVectorsPCA(1, 2) + cp.y;
    pcZ.z = sc1 * eigenVectorsPCA(2, 2) + cp.z;

	//Rectangular vertex 
	pcl::PointCloud<PointType>::Ptr transVertexCloud(new pcl::PointCloud<PointType>);//存放变换后点云包围盒的6个顶点
	pcl::PointCloud<PointType>::Ptr VertexCloud(new pcl::PointCloud<PointType>);//存放原来点云中包围盒的6个顶点
	transVertexCloud->width = 6;  
	transVertexCloud->height = 1;     
	transVertexCloud->is_dense = false;  
	transVertexCloud->points.resize(transVertexCloud->width * transVertexCloud->height);  
	transVertexCloud->points[0].x = max_p1.x;
	transVertexCloud->points[0].y = max_p1.y;
	transVertexCloud->points[0].z = max_p1.z;
	transVertexCloud->points[1].x = max_p1.x;
	transVertexCloud->points[1].y = max_p1.y;
	transVertexCloud->points[1].z = min_p1.z;
	transVertexCloud->points[2].x = max_p1.x;
	transVertexCloud->points[2].y = min_p1.y;
	transVertexCloud->points[2].z = min_p1.z;
	transVertexCloud->points[3].x = min_p1.x;
	transVertexCloud->points[3].y = max_p1.y;
	transVertexCloud->points[3].z = max_p1.z;
	transVertexCloud->points[4].x = min_p1.x;
	transVertexCloud->points[4].y = min_p1.y;
	transVertexCloud->points[4].z = max_p1.z;
	transVertexCloud->points[5].x = min_p1.x;
	transVertexCloud->points[5].y = min_p1.y;
	transVertexCloud->points[5].z = min_p1.z;
	pcl::transformPointCloud(*transVertexCloud, *VertexCloud, tm_inv);
	
	// 逆变换回来的角度
	cout << whd1(0) << " "<< whd1(1) << " " << whd1(2) << endl;
	auto euler = bboxQ1.toRotationMatrix().eulerAngles(0, 1, 2); 
	std::cout << "Euler from quaternion in roll, pitch, yaw"<< std::endl << euler/3.14*180 << std::endl<<std::endl;
	
	//Output time consumption 
	std::cout << "运行时间" << time.getTime() << "ms" << std::endl;

    //visualization
    pcl::visualization::PCLVisualizer viewer;
    pcl::visualization::PointCloudColorHandlerCustom<PointType> tc_handler(transformedCloud, 0, 255, 0); //设置点云颜色
	//Visual transformed point cloud
    viewer.addPointCloud(transformedCloud, tc_handler, "transformCloud");
    viewer.addCube(bboxT1, bboxQ1, whd1(0), whd1(1), whd1(2), "bbox1");
    viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_REPRESENTATION, pcl::visualization::PCL_VISUALIZER_REPRESENTATION_WIREFRAME, "bbox1");
    viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 0.0, 1.0, 0.0, "bbox1");

    viewer.addArrow(pcaX, op, 1.0, 0.0, 0.0, false, "arrow_X");
    viewer.addArrow(pcaY, op, 0.0, 1.0, 0.0, false, "arrow_Y");
    viewer.addArrow(pcaZ, op, 0.0, 0.0, 1.0, false, "arrow_Z");

    pcl::visualization::PointCloudColorHandlerCustom<PointType> color_handler(cloud, 255, 0, 0);  
    viewer.addPointCloud(cloud, color_handler, "cloud");
    viewer.addCube(bboxT, bboxQ, whd(0), whd(1), whd(2), "bbox");
    viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_REPRESENTATION, pcl::visualization::PCL_VISUALIZER_REPRESENTATION_WIREFRAME, "bbox");
    viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 1.0, 0.0, 0.0, "bbox");

    viewer.addArrow(pcX, cp, 1.0, 0.0, 0.0, false, "arrow_x");
    viewer.addArrow(pcY, cp, 0.0, 1.0, 0.0, false, "arrow_y");
    viewer.addArrow(pcZ, cp, 0.0, 0.0, 1.0, false, "arrow_z");

    viewer.addCoordinateSystem(0.5f*sc1);
    viewer.setBackgroundColor(0.0, 0.0, 0.0);

	viewer.addPointCloud(VertexCloud, "temp_cloud");
	viewer.setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 10, "temp_cloud");
    while (!viewer.wasStopped())
    {
          viewer.spinOnce();
    }

    return 0;
}

4.代码编译

  在次使用的是CMake编译,因此需要添加CMakeLists.txt文件后才可以进行编译

mkdir build
cd build
cmake ..
make

5.运行

运行时记得在后面加上点云文件的名字,代码里面支持’.pcd’格式和’.txt’格式,其它格式需要自己编写读取代码.’.txt’格式的文件中点云格式如下,一行代表一个点的坐标,横轴、纵轴、竖轴坐标之间加空格隔开:

point1.x point1.y point1.z
point2.x point2.y point2.z
...
pointN.x pointN.y pointN.z

运行命令如下

./rectangular_bounding_box ../milk.pcd 

6.效果图

2维点云包围盒效果图

---

3维点云包围盒效果图

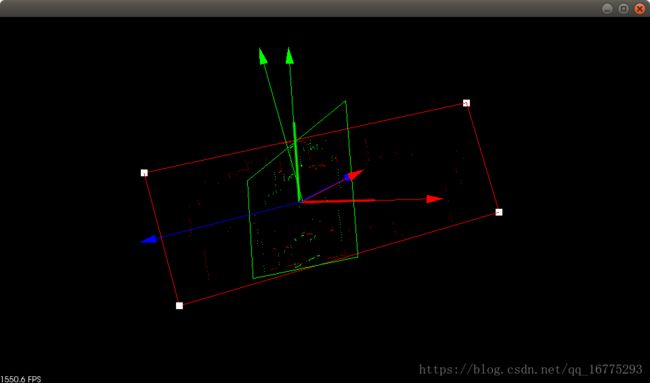
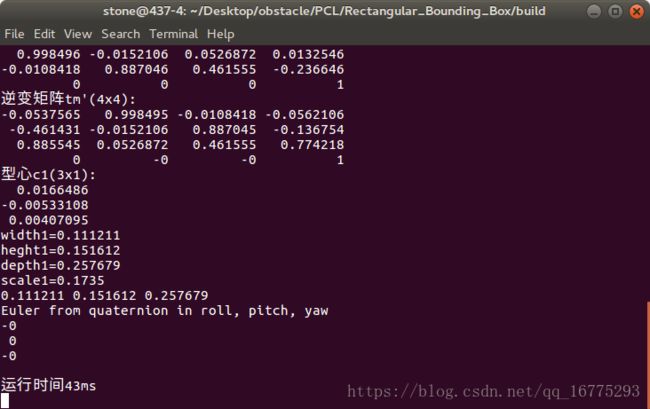
3维点云包围盒运行时间图

7.完整代码下载

  如果不想自己写“CMakeLists.txt”的朋友可以下完整的代码，点击这里下载，包括“.cpp”文件，“CMakeLists.txt”文件。