降维方法总结（线性与非线性）
文章目录
- 线性映射方法
- 主成分分析(PCA)
- 因子分析
- 流形学习
- 核化线性（KPCA）降维
- t-SNE
- 多维标度法（MDS）
- 等距离映射(Isomap)
- 局部线性嵌入（LLE）
线性映射方法
以下方法为基于线性映射处理线性数据的方法。
主成分分析(PCA)
关于PCA的原理以及实现在PCA主成分分析已经详细叙述，这里不做叙述。
因子分析
关于因子分析的愿意以及实现在因子分析(Factor Analyse)推导以及R语言实现已经详细叙述，这里不做叙述。
流形学习
核化线性（KPCA）降维
是一种非线性映射的方法，核主成分分析是对PCA的一种推广。KPCA主要利用了核函数，即对于当前非线性不可分数据，将其映射至更高维的空间至线性可分，再进行降维，而其中利用核函数可求得内积，进而得到样本在特征向量上的投影。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets,decomposition,manifold
def load_data():
iris=datasets.load_iris()
return iris.data,iris.target
def test_KPCA(*data):
X,Y=data
kernels=['linear','poly','rbf','sigmoid']
for kernel in kernels:
kpca=decomposition.KernelPCA(n_components=None,kernel=kernel)
kpca.fit(X)
print("kernel=%s-->lambdas:%s"%(kernel,kpca.lambdas_))
def plot_KPCA(*data):
X,Y=data
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
fig=plt.figure()
colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),(0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)
for i,kernel in enumerate(kernels):
kpca=decomposition.KernelPCA(n_components=2,kernel=kernel)
kpca.fit(X)
X_r=kpca.transform(X)
ax=fig.add_subplot(2,2,i+1)
for label,color in zip(np.unique(Y),colors):
position=Y==label
ax.scatter(X_r[position,0],X_r[position,1],label="target=%d"%label,color=color)
ax.set_xlabel("X[0]")
ax.set_ylabel("X[1]")
ax.legend(loc="best")
ax.set_title("kernel=%s"%kernel)
plt.suptitle("KPCA")
plt.show()
X,Y=load_data()
test_KPCA(X,Y)
plot_KPCA(X,Y)
不同的核函数，其降维后的数据分布是不同的
t-SNE
这篇博客写的特别好可以参考原理从SNE到t-SNE再到LargeVis
多维标度法（MDS）
MDS的核心是：保证所有数据点对在低维空间中的距离等于在高维空间中的距离。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets,decomposition,manifold
def load_data():
iris=datasets.load_iris()
return iris.data,iris.target
def test_MDS(*data):
X,Y=data
for n in [4,3,2,1]:
mds=manifold.MDS(n_components=n)
mds.fit(X)
print("stress(n_components=%d):%s"%(n,str(mds.stress_)))
def plot_MDS(*data):
X,Y=data
mds=manifold.MDS(n_components=2)
X_r=mds.fit_transform(X)
# print(X_r)
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),(0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)
for label,color in zip(np.unique(Y),colors):
position=Y==label
ax.scatter(X_r[position,0],X_r[position,1],label="target=%d"%label,color=color)
ax.set_xlabel("X[0]")
ax.set_ylabel("Y[0]")
ax.legend(loc="best")
ax.set_title("MDS")
plt.show()
X,Y=load_data()
test_MDS(X,Y)
plot_MDS(X,Y)
其中stress输出原始数据降维后的距离误差之和
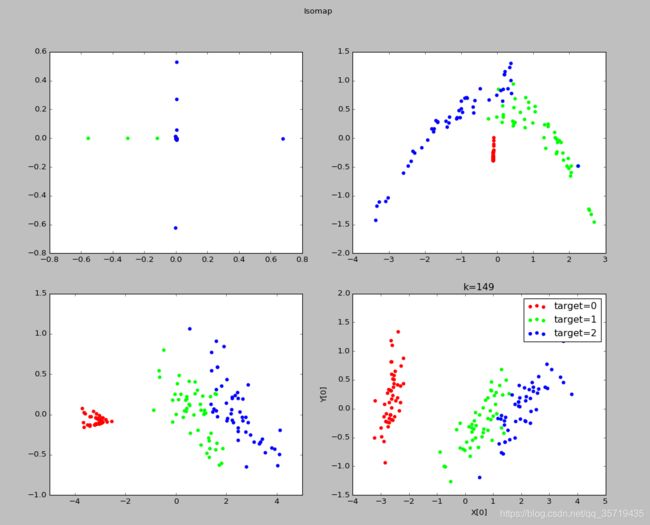
等距离映射(Isomap)
输入：样本集D，近邻参数k，低维空间维数n’
输出：样本集在低维空间中的矩阵Z
算法步骤：
- 对每个样本点x，计算它的k近邻；同时将x与它的k近邻的距离设置为欧氏距离，与其他点的距离设置为无穷大
- 调用最短路径算法计算任意两个样本点之间的距离，获得距离矩阵D
- 调用多维缩放MDS算法，获得样本集在低维空间中的矩阵Z
注：新样本难以将其映射到低维空间中，因此需要训练一个回归学习器来对新样本的低维空间进行预测建立近邻图时，要控制好距离的阈值，防止短路和断路。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets,decomposition,manifold
def load_data():
iris=datasets.load_iris()
return iris.data,iris.target
def test_Isomap(*data):
X,Y=data
for n in [4,3,2,1]:
isomap=manifold.Isomap(n_components=n)
isomap.fit(X)
print("reconstruction_error(n_components=%d):%s"%(n,isomap.reconstruction_error()))
def plot_Isomap_k(*data):
X,Y=data
Ks=[1,5,25,Y.size-1]
fig=plt.figure()
# colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),(0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)
for i,k in enumerate(Ks):
isomap=manifold.Isomap(n_components=2,n_neighbors=k)
X_r=isomap.fit_transform(X)
ax=fig.add_subplot(2,2,i+1)
colors = ((1, 0, 0), (0, 1, 0), (0, 0, 1), (0.5, 0.5, 0), (0, 0.5, 0.5), (0.5, 0, 0.5), (0.4, 0.6, 0), (0.6, 0.4, 0),
(0, 0.6, 0.4), (0.5, 0.3, 0.2),)
for label,color in zip(np.unique(Y),colors):
position=Y==label
ax.scatter(X_r[position,0],X_r[position,1],label="target=%d"%label,color=color)
ax.set_xlabel("X[0]")
ax.set_ylabel("Y[0]")
ax.legend(loc="best")
ax.set_title("k=%d"%k)
plt.suptitle("Isomap")
plt.show()
X,Y=load_data()
test_Isomap(X,Y)
plot_Isomap_k(X,Y)
可以看出k=1时，近邻范围过小，此时发生断路现象
局部线性嵌入（LLE）
LLE算法认为每一个数据点都可以由其近邻点的线性加权组合构造得到。算法的主要步骤分为三步：
- 寻找每个样本点的k个近邻点；
- 由每个样本点的近邻点计算出该样本点的局部重建权值矩阵；
- 由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。
具体的算法流程如图2所示：
LLE可以说是流形学习方法最经典的工作之一。很多后续的流形学习、降维方法都与LLE有密切联系。因此以下详细叙述算法流程。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets,decomposition,manifold
def load_data():
iris=datasets.load_iris()
return iris.data,iris.target
def test_LocallyLinearEmbedding(*data):
X,Y=data
for n in [4,3,2,1]:
lle=manifold.LocallyLinearEmbedding(n_components=n)
lle.fit(X)
print("reconstruction_error_(n_components=%d):%s"%(n,lle.reconstruction_error_))
def plot_LocallyLinearEmbedding_k(*data):
X,Y=data
Ks=[1,5,25,Y.size-1]
fig=plt.figure()
# colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),(0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)
for i,k in enumerate(Ks):
lle=manifold.LocallyLinearEmbedding(n_components=2,n_neighbors=k)
X_r=lle.fit_transform(X)
ax=fig.add_subplot(2,2,i+1)
colors = ((1, 0, 0), (0, 1, 0), (0, 0, 1), (0.5, 0.5, 0), (0, 0.5, 0.5), (0.5, 0, 0.5), (0.4, 0.6, 0), (0.6, 0.4, 0),
(0, 0.6, 0.4), (0.5, 0.3, 0.2),)
for label,color in zip(np.unique(Y),colors):
position=Y==label
ax.scatter(X_r[position,0],X_r[position,1],label="target=%d"%label,color=color)
ax.set_xlabel("X[0]")
ax.set_ylabel("Y[0]")
ax.legend(loc="best")
ax.set_title("k=%d"%k)
plt.suptitle("LocallyLinearEmbedding")
plt.show()
X,Y=load_data()
test_LocallyLinearEmbedding(X,Y)
plot_LocallyLinearEmbedding_k(X,Y)
其中reconstruction_error_为重构后的总误差。
