ICPC Arab Collegiate Programming Contest 2013

今天有一场比赛，虽然是复现的2013年的某一场比赛，十二点到五点，今天出奇的顺利，三点半我们三人就愉快的决定提前下班了 哈哈哈哈哈。
不过说实话这场比赛应该是水题很多，，，，，
都有题号，现在这些题目都被UVa收录，可以测评

A.The Alphabet Sticker UVALive - 6754

When we were kids, we used to play with some stickers where these stickers contain some (but not
necessarily all) lower case English alphabet letters.
Each sticker contains some letters arranged in a single row, where all occurrences of the same letter
are adjacent to each other. A sticker can be represented as a string of characters, for example the
following are valid stickers’ representations: “aabcc”, “ccccab” and “mmaw”. And the following are not
valid (because not all occurrences of the same letter are adjacent to each other): “abacc”, “cccabc”
and “mawm”.
Now we found some stickers with some missing letters, but we are sure that all missing letters
belong to the visible letters set (that is, for every missing letter, there is at least one visible letter that
matches the missing one). In this problem a question mark letter represents a missing letter. Given
some stickers’ representations with zero or more missing letters, your task is to count the number of
possible original configurations for each sticker.
For example, this sticker “aa??bb” with missing letters could have been one of the following original
stickers “aaaabb”, “aaabbb” or “aabbbb”. But it could not have been any of the following original
stickers “aababb” (it is invalid sticker) and “aaccbb” (because the letter ‘c’ did not appear in the given
configuration).
Input
Your program will be tested on one or more test cases. The first line of the input will be a single integer
T, the number of test cases (1 ≤ T ≤ 100). Followed by the test cases, each test case is described in
one line which contains a non-empty string which consists of up to 10,000 letters, each letter is either
a lower case English letter (from ‘a’ to ‘z’) or a question mark (‘?’). This string represents a sticker
configuration which contains zero or more question marks, it will also contain at least one letter which
is not a question mark and there will be at least one valid original configuration for it.
Output
For each test case, print a single line which contains a single integer representing the number of possible
original configurations for the sticker, since the result may be very large, print it modulo 1,000,000,007
(109 + 7).
Sample Input
4
aa??bb
aaccbb
?a?
a??a
Sample Output
3
1
1
1

A题我没做，就拿来发一下呗，嘻嘻嘻，看码风也知道不是我写的，我没补题，也不想补了，，，

#include 
using namespace std;

const int mod = 1e9 + 7;

int main() {
    int T;	cin >> T;
    while (T--) {
        string s;	cin >> s;
        unsigned long long ans = 1;
        int a = 0, b = s.length() - 1;
        while (s[a] == '?')	++a;
        while (s[b] == '?') --b;
        for (int i = a; i <= b; ++i) {
            if (s[i] == '?') {
                int t = i;
                while (s[t] == '?')		++t;
                if (s[i-1] != s[t]) 	ans = (ans * ((t - i + 1) % mod)) % mod;
                i = t;
            }
        }
        cout << ans << endl;
    }
    return 0;
}

C.Increasing Shortest Path UVALive - 6756

We all love short and direct problems, it is easier to write, read and understand the problem statement.
Here is one of these problems. “Life is too short to make a story”, said Ahmed Aly.
You are given a weighted directed graph of N nodes (the nodes are numbered from 1 to N), where
the weights of the edges are distinct and positive. For each graph, you are also given a list of queries
to answer.
Each query will be represented by 3 integers A B C, which means you need to find the shortest
path (the path with minimum sum of weights of its edges) which goes from node A to node B and uses
at most C edges, such that the weights of the edges in that path are in increasing order along the path,
which means the weight of each edge in that path should be greater than the weight of the edge before
it (unless it is the first edge in the path).
Your task is to write a program which answers these queries.
Input
Your program will be tested on one or more test cases. The first line of the input will be a single
integer T, the number of test cases (1 ≤ T ≤ 100). Followed by the test cases, the first line of each
test case contains 3 integers separated by a single space N M Q (2 ≤ N ≤ 150), (0 ≤ M ≤ 3, 000) and
(1 ≤ Q ≤ 1, 000) representing the number of nodes, the number of edges and the number of queries,
respectively. Followed by M lines, each line contains 3 integers separated by a single space X Y Z
(1 ≤ X, Y ≤ N) (1 ≤ Z ≤ 3, 000) which represent an edge going from the node X to the node Y with
cost Z (X and Y will be different). Followed by Q lines, each line contains 3 integers separated by a
single space A B C (1 ≤ A, B ≤ N) (0 ≤ C ≤ M) which represent a query as described above (A and
B will be different).
Note that there might multiple edges between the same pair of nodes.
Output
For each test case, print a single line for each query which contains a single integer, the minimum sum
of weights for a path between the given pair of nodes which satisfies the given constraints, or ‘-1’ if
there is no valid path between the given nodes which satisfies the given constraints. The output must
not contain empty lines between the cases.
Sample Input
1
8 9 3
1 2 1
2 3 2
3 4 3
4 5 12
5 8 7
1 6 8
6 4 9
1 7 5
7 4 4
1 4 2
1 4 3
1 4 1
Sample Output
17
6
-1

题目解析：
这个题稍微说一下，这个题是我写的，但是也是当时卡了时间最长的题，dis[i][j][k]表示从i到j走了k条边的最短路径，剩下的就看代码就很清楚了。

#include 
#include 
#include 
#include 
#include 
using namespace std;
#define Maxn 152
int dis[Maxn][Maxn][Maxn];
struct Edge{
    int u,v,w;
}e[3005];

inline bool cmp(Edge A,Edge B) {
    return A.w < B.w;
}

int main(int argc,char* argv[]) {
    int n,m,Q,T,u,v,w; scanf("%d",&T);
    while(T--) {
        scanf("%d %d %d",&n,&m,&Q);
        memset(dis,-1,sizeof(dis));
        for(int i=0; i<=n; i++) dis[i][i][0] = 0;
        for(int i=1; i<=m; i++) {
            scanf("%d %d %d",&u,&v,&w);
            e[i].u = u,e[i].v = v,e[i].w = w;
            //dis[u][v][1] = w;
        }
        sort(e + 1,e + m + 1,cmp);// 排序之后   在进行如下的状态更新 可以保证后面的边权大于前一条
        for(int i=1; i<=m; i++) {
            for(int j=1; j<=n; j++)
                for(int k=1; k<n; k++){
                    if(dis[j][e[i].u][k - 1] != -1) { // j --> e[i].u 
                        if(dis[j][e[i].v][k] == -1) dis[j][e[i].v][k] = dis[j][e[i].u][k - 1] + e[i].w;
                        else dis[j][e[i].v][k] = min(dis[j][e[i].u][k - 1] + e[i].w,dis[j][e[i].v][k]);
                    }
                }
        }
        while(Q --) {
            scanf("%d %d %d",&u,&v,&w);
            int Ans = -1;
            for(int i=0; i<=min(n-1,w); i++)
                if(dis[u][v][i] != -1) {
                    if(Ans == -1) Ans = dis[u][v][i];
                    else Ans = min(Ans,dis[u][v][i]);
                }
            printf("%d\n",Ans);
        }
    }
    return 0;
}

// 这是当时一分怎么改都是WA的代码，路过的大神帮忙指点江山吧
#include 
#include 
#include 
#include 
#include 
using namespace std;
#define Maxn 151
// 不多于C 条边    假设C小于最少边数 则-1    否则c好像没有什么用
int dis[Maxn][Maxn][Maxn];
struct Edge{
    int u,v,w;
}e[3005];

inline bool cmp(Edge A,Edge B) {
    return A.w < B.w;
}

int main(int argc,char* argv[]) {
    int n,m,Q,T,u,v,w; scanf("%d",&T);
    while(T--) {
        scanf("%d %d %d",&n,&m,&Q);
        memset(dis,-1,sizeof(dis));
        for(int i=1; i<=n; i++) dis[i][i][0] = 0;
        for(int i=1; i<=m; i++) {
            scanf("%d %d %d",&u,&v,&w);
            e[i].u = u,e[i].v = v,e[i].w = w;
            //dis[u][v][1] = w;
        }

        // 边由小到大排序
        sort(e + 1,e + m + 1,cmp);// 不排序应该是也行的吧

        //
        for(int i=1; i<=m; i++) {
            for(int j=1; j<=n; j++)
                for(int k=1; k<n; k++){// 最多途径n-1条边
                    if(dis[j][e[i].u][k - 1] != -1) { // j --> e[i].u  用了k-1条边   不等于-1  就是通路
                        if(dis[j][e[i].v][k] == -1 || dis[j][e[i].v][k] > dis[j][e[i].u][k - 1]) dis[j][e[i].v][k] = dis[j][e[i].u][k - 1] + e[i].w;
                        else dis[j][e[i].v][k] = min(dis[j][e[i].u][k - 1] + e[i].w,dis[j][e[i].v][k]);
                    }
                }
        }
        while(Q --) {
            scanf("%d %d %d",&u,&v,&w);
            int Ans = 0x7f;
            for(int i=0; i<=min(n-1,w); i++)
                if(dis[u][v][i] != -1)
                    Ans = min(Ans,dis[u][v][i]);
            printf("%d\n",(Ans == 0x7f ? -1 : Ans));
        }
    }
    return 0;
}

E.Balloons Colors UVALive - 6758

Assigning a balloon color to each problem is one of the tasks we need to do every year, and sometimes
it is tricky.
We noticed that some contestants assume some colors for some problems according to the difficulty.
For example, the easiest problem is the red one and the hardest problem is the black one.
We do not want these assumptions to be true, so we decided to add constraints for the easiest and
the hardest problems.
There are N problems, numbered from 1 to N, the easiest problem is problem number 1, and the
hardest problem is problem number N. Also there are N unique colors, for simplicity we will give each
color a unique number from 1 to N.
We want to assign each color to exactly 1 problem, such that the easiest problem does not get the
color X and the hardest problem does not get the color Y .
Given N, X, Y and an assignment of the colors, your task is to find if this assignment satisfies the
above conditions or not.
Input
Your program will be tested on one or more test cases. The first line of the input will be a single
integer T, the number of test cases (1 ≤ T ≤ 100). Followed by the test cases, the first line of each
test case contains 3 integers separated by a single space N X Y (3 ≤ N ≤ 100) and (1 ≤ X, Y ≤ N)
representing the number of problems, the color which the easiest problem should not get and the color
which the hardest problem should not get, respectively. Followed by a line which contains N integers
separated by a single space (each integer from 1 to N should appear exactly once), the first integer is
the color for the first problem (the easiest), the second integer is the color for the second problem and
so on (the last integer is the color for the hardest problem).
Output
For each test case, print a single line which contains a single word, this word should be (without the
quotes):

• ‘BOTH’: If both the easiest and hardest problems got colors which they should not get.
• ‘EASY’: If only the easiest problem got a color which it should not get.
• ‘HARD’: If only the hardest problem got a color which it should not get.
• ‘OKAY’: If both the easiest and hardest problems got colors which they can get.
  Sample Input
  4
  3 1 2
  1 3 2
  5 3 4
  3 1 2 4 5
  6 1 6
  2 1 3 4 5 6
  7 7 7
  1 7 2 3 4 5 6
  Sample Output
  BOTH
  EASY
  HARD
  OKAY

题目分析
就sb题，好好翻译，英语好的人应该很快都AC了，除非没看的…

#include
#include
#include
using namespace std;

int main(int argc,char* argv[]) {
    int T,n,X,Y,temp; scanf("%d",&T);
    while(T--) {
        scanf("%d %d %d",&n,&X,&Y);
        int op1 = 0,op2 = 0;
        for(int i=1; i<=n; i++) {
            scanf("%d",&temp);
            if(i == 1 && temp == X) op1 = 1;
            if(i == n && temp == Y) op2 = 1;
        }
        if(op1 && op2) printf("BOTH\n");
        else if (op1 && !op2) puts("EASY");
        else if (op2 && !op1) puts("HARD");
        else puts("OKAY");

    }

    return 0;
}

F.NASSA’s Robot UVALive - 6759

NASSA’s robot landed on Mars. The place where it landed can be modeled as an infinite 2-dimensional
plane with perpendicular X-axis and Y -axis coordinates.
The robot continuously reports its location back to Earth, but due to a serious design flaw, it only
reports the moves it makes instead of the coordinates of its exact location. Some signals went missing
and never reached our reception.
In one of the space exploration missions, the robot sent a sequence of signals, which can be represented by a string composed of the following characters: ‘U’, ‘R’, ‘D’, ‘L’ or ‘?’. ‘U’ represents up
(Y -coordinate increases by 1), ‘R’ represents right (X-coordinate increases by 1), ‘D’ represents down
(Y -coordinate decreases by 1), ‘L’ represents left (X-coordinate decreases by 1) and ‘?’ represents
a missed signal. Every character in the sequence is a single step in the corresponding direction. A
missed signal is a single step in one of the four directions. The robot is initially at X-coordinate 0 and
Y -coordinate 0 before starting to send the given signals.
After sending some signals while the robot is moving, its software crashed and the robot could
not do any further moves. The researchers on the base want to limit the space where they can look
for the robot. In other words, they want to find the minimum possible X-coordinate, the minimum
possible Y -coordinate, the maximum possible X-coordinate and the maximum possible Y -coordinate
of the current location of the robot.
Input
Your program will be tested on one or more test cases. The first line of the input will be a single integer
T, the number of test cases (1 ≤ T ≤ 100). Followed by the test cases, each test case is described in
one line which contains a non-empty string which consists of up to 100,000 letters, each letter is ‘U’,
‘R’, ‘D’, ‘L’ or ‘?’. This string represents the sequence of signals as described above.
Output
For each test case, print a single line which contains 4 integers separated by a single space, which
are the minimum possible X-coordinate, the minimum possible Y -coordinate, the maximum possible
X-coordinate and the maximum possible Y -coordinate for the location of the robot after it stopped
moving.
Sample Input
3
RUL?R?D
???
RRRUU
Sample Output
-1 -2 3 2
-8 -8 8 8
3 2 3 2

#include
#include
#include
using namespace std;
#define Maxn 100005
char s[Maxn];
int main(int argc,char* argv[]) {
	int T,n,X,Y,temp; scanf("%d",&T);
	while(T--) {
		scanf("%s",s + 1);
		int len = strlen(s + 1);
		int R = 0, L = 0,U = 0, D = 0,Num = 0;
		for(int i=1; i<=len; i++) {
			if(s[i] == 'R') R++;
			if(s[i] == 'L') L++;
			if(s[i] == 'U') U++;
			if(s[i] == 'D') D++;
			if(s[i] == '?') Num ++;
		}
		printf("%d %d %d %d\n",R - L - Num,U - D - Num,R - L + Num,U - D + Num);
	}
	
	return 0;
}

G.The Stones Game UVALive - 6760

The stones game is a simple game, it is also a very old game which is unknown to almost everyone.
The game starts with N stones and M players, the players are numbered from 1 to M. The players
play in turns, player number 1 plays first, then player number 2 and so on until player number M plays,
after this player number 1 plays again and they keep playing until the end of the game.
For each turn, the players do the following 2 steps:

1. The player gets a chance to remove a stone, and he/she should remove a stone in this step if
   he/she decided to do so.
2. Regardless of the decision of the current player (whether or not he/she removed a stone in the
   first step), if this is not the first turn and in the previous turn the player decided not to remove
   a stone in his/her first step, then the current player must remove a stone in this step (if in the
   previous turn the player decided to remove a stone in his/her first step, then the current player
   must not remove a stone in this step).
   This means in some turns a player might remove 0, 1 or 2 stones according to the above rules. In
   this game, the player who removes the last stone wins the game.
   Now you are given the total number of stones, the total number of players and a player number and
   you are asked to answer the following question:
   Is there a strategy for this player to win the game regardless of the actions taken by the other
   players in their turns?
   Input
   Your program will be tested on one or more test cases. The first line of the input will be a single integer
   T, the number of test cases (1 ≤ T ≤ 100). Followed by the test cases, each test case is described in one
   line which contains 3 integers separated by a single space N M X (1 ≤ N, M ≤ 109
   ) and (1 ≤ X ≤ M)
   representing the number of stones, the number of players and the player number, respectively.
   Output
   For each test case, print a single line which contains a single word, this word is either ‘YES’ or ‘NO’
   (without the quotes) representing the answer for the above question for the given player number.
   Sample Input
   2
   2 2 2
   2 2 1
   Sample Output
   YES
   NO

// 这个题也是队友写的，我最早读完题 这题博弈论 好了，然后丢给队友了
// 哈哈哈哈
#include
using namespace std;

int main()
{
    int T,n,m,k;
    cin >> T;
    while (T--){
        cin >> n >> m >> k;
        if (k > n) 
			cout << "NO" <<endl;
        else { 
			if (n % m == k || (n % m == 0 && m == k)) 
				cout << "YES" << endl;
       		else  
				cout << "NO" << endl;
		} 
    }
    return 0;
}

I.Omar Loves Candies UVALive - 6762

Omar loves to eat a lot of candies, but unfortunately most of the candies are not healthy. So his parents
found a way to give each candy a score, a higher score means a healthier candy (the score is an integer
that can be positive, zero or negative).
One day he went with his parents to buy some candies, and they found a strange store where all
the candies are stored in a 2-dimensional grid of N rows with M candies in each row. The rows are
numbered from 1 to N from top to bottom, and the columns are numbered from 1 to M from left to
right and every cell contains one candy.
They noticed something else, any candy (except for those in the first row) is healthier than the
candy which is exactly above it, and any candy (except for those in the first column) is healthier than
the candy which is exactly to its left (healthier means having higher score as defined above).
There is one more strange thing about this store, to buy some candies you have to select a subrectangle of the candies’ grid and buy all the candies within this sub-rectangle.
Omar’s parents want to select a non-empty sub-rectangle that has the maximum sum of candies’
scores among all possible sub-rectangles.
For example, consider the grid in the example input. Some of the possible sub-rectangles of candies
they can select are [-2, -1, 2, 3], [-4, -2, -1] or [2, 3, 4, 5]. The last sub-rectangle has the maximum
sum of scores, which is 14. They can not select the following lists of candies [1, 2, 3, 4, 5] or [-2, -1, 2]
(because these lists do not form a sub-rectangle of the given grid).

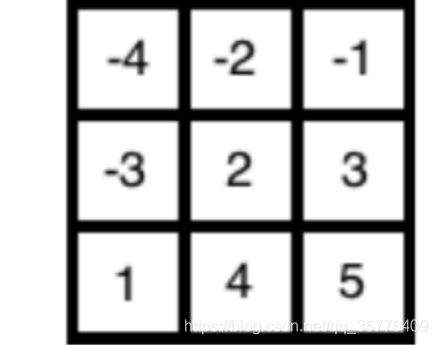
Can you help them by writing a program which finds the non-empty sub-rectangle with the maximum
possible sum of scores in the given grid?
Input
Your program will be tested on one or more test cases. The first line of the input will be a single
integer T, the number of test cases (1 ≤ T ≤ 100). Followed by the test cases, each test case starts
with a line containing two integers separated by a single space N M (1 ≤ N, M ≤ 1, 000) representing
the dimensions of the candies’ grid, followed by N lines, each one contains M integers separated by a
single space, representing the candies’ scores in this row. The given grid representation will satisfy the
conditions mentioned above, and each integer in the grid will not be less than -2,000 and will not be
greater than 2,000.
Output
For each test case, print a single line which contains a single integer representing the maximum sum of
scores they can get from a non-empty sub-rectangle.
Sample Input
1
3 3
-4 -2 -1
-3 2 3
1 4 5
Sample Output
14

题目分析：
这个大水题 也是我发现的，二位前缀和，一直选取到右下角肯定更优

#include
#include
#include
using namespace std;
#define Maxn 1005
#define LL long long
LL sum[Maxn][Maxn];
int a[Maxn][Maxn];
int main(int argc,char* argv[]) {
	int T,n,X,Y,temp,m; scanf("%d",&T);
	while(T--) {
		scanf("%d %d",&n,&m);
		for(int i=1; i<=n; i++)
			for(int j=1; j<=m; j++) {
				scanf("%d",&a[i][j]);
				sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
			}
		LL Ans = -2000*1000;
		for(int i=1; i<=n; i++) 
			for(int j=1; j<=m; j++) {
				Ans = max(Ans,sum[n][m] + sum[i - 1][j - 1] - sum[i - 1][m] - sum[n][j - 1]);
			} 
		
		printf("%d\n",Ans);
	}
	
	return 0;
}

J.Modified LCS UVALive - 6763

LCS stands for longest common subsequence, and it is a well known problem. A sequence in this
problem means a list of integers, and a sequence X is considered a subsequence of another sequence Y ,
when the sequence X can be obtained by deleting zero or more elements from the sequence Y without
changing the order of the remaining elements.
In this problem you are given two sequences and your task is to find the length of the longest
sequence which is a subsequence of both the given sequences.
You are not given the sequences themselves. For each sequence you are given three integers N, F
and D, where N is the length of the sequence, F is the first element in the sequence. Each element
except the first element is greater than the element before it by D.
For example N = 5, F = 3 and D = 4 represents the following sequence: [3, 7, 11, 15, 19].
There will be at least one integer which belongs to both sequences and it is not greater than
1,000,000.
Input
Your program will be tested on one or more test cases. The first line of the input will be a single integer
T, the number of test cases (1 ≤ T ≤ 100). Followed by the test cases, each test case is described in one
line which contains 6 integers separated by a single space N1 F1 D1 N2 F2 D2 (1 ≤ N1, N2 ≤ 1018)
and (1 ≤ F1, D1, F2, D2 ≤ 109
) representing the length of the first sequence, the first element in the
first sequence, the incremental value of the first sequence, the length of the second sequence, the first
element in the second sequence and the incremental value of the second sequence, respectively.
Output
For each test case, print a single line which contains a single integer representing the length of the
longest common subsequence between the given two sequences.
Sample Input
3
5 3 4 15 3 1
10 2 2 7 3 3
100 1 1 100 1 2
Sample Output
4
3
50

这个题也是队友写的，本来还想补一补的，唉算了，

#include 
#include 
#include 
#include 
#include 
#include 
#include
using namespace std; 
#define ll  long long 
void gcd(ll a, ll b, ll& d, ll& x, ll& y) { 
    if(!b) {
		d = a; 
		x = 1; 
		y = 0;
	} 
    else{ 
		gcd(b, a%b, d, y, x); 
		y -= x*(a/b);
	} 
} 

int T;

int main() { 
    ll n1,f1,d1,n2,f2,d2; 
    cin >> T; 
    while(T--) { 
        cin >> n1 >> f1 >> d1 >> n2 >> f2 >> d2;
        ll x,y,g; 
        gcd(d1,-d2,g,x,y); 
        ll f = f2-f1; 
        x *= f / g;
        y *= f / g; 
        g = abs(g); 
        ll a = d1 / g; 
        ll b = d2 / g; 
        if(x < 0 || y < 0) { 
            while(x < 0 || y < 0) { 
                x += b; 
                y += a; 
            } 
        } 
        else{
            while(x >= 0 && y >= 0) { 
                x -= b; 
                y -= a; 
            } 
            x += b; 
            y += a; 
        } 
        ll num1 = (n1-1-x) / b; 
        ll num2 = (n2-1-y) / a; 
        ll num = min(num1, num2) + 1;
        cout << num << endl;
    } 
    return 0; 
}