单调递增子序列
前言：最长公共子序列
子序列可以不连续，但是有先后的次序关系.
为啥不能使用暴力解决这个问题：设A串长为n, B串长为m。A串子序列个数
, B串子序列个数
, 针对每一种情况进行匹配，时间复杂度变为：
.
所以利用动态规划：
A = {a, b, c, 1, 2, 3, a, b, c}
B = {1, 2, 3, a, d, c}
定义状态:
dp[i][j]: A串第i个位置，B串第j个位置前的两个序列的最大公共子序列.
状态转移方程:
①A[i] == B[j] -> dp[i][j] = dp[i-1][j-1] + 1
explanation:
字符串匹配时:i, j位置之前的最长公共子序列就是i-1, j-1位置之前的长度+1
②A[i] != B[j] -> dp[i][j] = max(dp[i-1][j], dp[i][j-1])
explanation:
字符串不匹配时，最长公共子序列的长度是不会变的，但是我们有两种选择，就是在[i，j-1]位置以前的和[i，j-1]位置以前的两种情况之中，选取最大的最长公共子序列作为当前的最长公共子序列即可.
练习题：NYOJ最长公共子序列
正文：单调递增子序列
为啥不能使用暴力解决这个问题：设A串长为n. A串子序列个数
,判断其是否递增,时间复杂度变为:
.
所以出现了三种求单调递增子序列的方式：两个
的方法可以求出递增的子序列是哪个，一个
的方法可以求出单调序列的最大长度
一、$o(n^2)$方法
1.转化成最长公共子序列求解
原序列为A，把A按升序排序得到序列B，求出A，B序列的最长公共子序列，即为A的最长单调递增子序列。
2.带有一定动态规划思想的
定义状态：
d[i]为以第i个元素结尾的最长递增子序列的长度
状态转移方程：
A[j] < A[i] : d[j] = max{d[i], d[j]+1}
对于每一个 i ，令 j 从 i-1 到0遍历，当 a[j] < a[i]，比较当前 d[i] 和每一个 d[j]+1 的大小，将最大值赋给 d[i]
(如果看不懂的话 让我们举一个例子吧~)
e.g.
5，3，4，8，6，7
+ 第一个数字5，d[0] = 1
+ 第一个数字3，前面没有比他还小的了，d[1] = 1
+ 第三个数字4，最长的递增子序列就是3，4，d[2] = 2
+ 第四个数组8，d[3] = 3
+ 第五个数字6，d[4] = 3, 此时的3是由d[2]+1
+ 第六个数字7，d[5] = 4
二、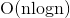
方法(二分+DP)
在上面的例子中：3 4 8 6相比于与 3 4 8 6 显然后者更优
此时的状态为：
d[x] = d[y], 但是 A[x] < A[y], 即选择x这个情况会比y这个情况好，在这种情况下保留x一定不会丢失最优解。所以对于相同的d[?]值，只需要保留A[i]较小的情况。
e.g. (A、d从1开始)
序列A = {2, 1, 5, 3, 6, 4, 8, 9, 7}
此时最长递增子序列(Longest Increasing Subsequence LIS) = 5
setp1: 把A[1]有序地放到d里，令d[1] = 2，就是说当只有1一个数字2的时候，长度为1的LIS的最小末尾是2。这时Len=1
setp2: 然后，把A[2]有序地放到d里，令d[1] = 1，就是说长度为1的LIS的最小末尾是1，A[1]=2已经没用了。这时Len=1
setp3: 接着，A[3] = 5，d[3] > d[1]，所以令d[3]=d[2]=d[3]=5，就是说长度为2的LIS的最小末尾是5，很容易理解吧。这时候B[1..2] = 1, 5，Len＝2
setp4: 再来，d[4] = 3，它正好加在1,5之间，放在1的位置显然不合适，因为1小于3，长度为1的LIS最小末尾应该是1，这样很容易推知，长度为2的LIS最小末尾是3，于是可以把5淘汰掉，这时候B[1..2] = 1, 3，Len = 2
setp5: 继续，d[5] = 6，它在3后面，因为B[2] = 3, 而6在3后面，于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6，还是很容易理解吧？ Len = 3 了噢。
setp6: 第6个, d[6] = 4，你看它在3和6之间，于是我们就可以把6替换掉，得到B[3] = 4。B[1..3] = 1, 3, 4， Len继续等于3
setp7: 第7个, d[7] = 8，它很大，比4大，嗯。于是B[4] = 8。Len变成4了
setp8: 第8个, d[8] = 9，得到B[5] = 9，嗯。Len继续增大，到5了。
setp9: 最后一个, d[9] = 7，它在B[3] = 4和B[4] = 8之间，所以我们知道，最新的B[4] =7，B[1..5] = 1, 3, 4, 7, 9，Len = 5。
于是我们知道了LIS的长度为5。
hhh大概很有可能觉得疑惑的地方就是 这里的 为什么这里的7能替换8？
这也是为什么说 只能通过这样的方法算出 单调递增子序列的长度 而不能求出该子序列本身 why?
Reasons are as follows:
此时取序列A = {2, 1, 5, 3, 6, 4, 8, 9, 7}
按照上述方式序列应该变为A = {1, 3, 4, 7, 9}但是这样显然不符合序列A的单调递增模式。
若此时取序列A = {2, 1, 5, 3, 6, 4, 8, 9, 7, 10, 11}
answer:{1, 3, 4, 7, 9, 10, 11}
real answer:{1, 3, 4, 8, 9, 10, 11}
若此时取序列A = {2, 1, 5, 3, 6, 4, 8, 9, 7, 9, 10}
answer:{1, 3, 4, 7, 9, 10}
real answer:{1, 3, 4, 7, 9, 10}
especially:
如果添加一个新数(即增加LIS的长度)，需要替换掉前面全部的数据，此时的序列为正确的序列
e.g.1. 若此时取序列A = {2, 1, 5, 3, 6, 4, 8, 9, 7, 8, 9}
answer:{1, 3, 4, 7, 8, 9}
real answer:{1, 3, 4, 7, 8, 9}
e.g.2. A={2, 4, 1, 3, 4, 0}
start: {2, 4}
setp1: {1, 4} 1替换2, 序列不正确 但是长度为2正确
setp2: {1, 3} 3替换4，序列正确，长度为2正确
setp3: {1, 3, 4} 4直接接在序列后，序列正确，长度为3正确 !!!此时增加了LIS长度 数据也都被替换完毕了 所以此时为正确的最长递增序列形式
setp4: {0, 3, 4} 0替换1，序列不正确，长度为3正确。
//先贴上别人的代码再说
#include
#include
#include
using namespace std;
#define mem(a,n) memset(a,n,sizeof(a))
const int N=1e3+5;
const int INF=0x3f3f3f3f;
int dp[N],a[N];
int main()
{
int n;
while(~scanf("%d",&n))
{
mem(dp,INF);
for(int i=0;i NYOJ:单调递增子序列
练习题1：单调递增子序列
Hihocoder:车队(需利用$O(nlogn)$才不会超时)
练习题：nlogn单调递增序列