【AtCoder】AtCoder Grand Contest 032 题解

【比赛链接】

• 点击打开链接

【题解链接】

• 点击打开链接

【A】 Limited Insertion

【思路要点】

• 考虑时间倒流，对于一个位置 $i$ ，若 $a_i=i$ ，则可以将其删去，问是否能将序列删空。
• 不难发现每次删除最大的 $i$ ，使得 $a_i=i$ 是唯一的最优策略，模拟之，若无法操作则无解。
• 时间复杂度 $O(N^2)$ 。

【代码】

#include
using namespace std;
const int MAXN = 2e5 + 5;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int n, a[MAXN], ans[MAXN];
int main() {
	read(n);
	for (int i = 1; i <= n; i++)
		read(a[i]);
	for (int i = n; i >= 1; i--) {
		int pos = 0;
		for (int j = 1; j <= i; j++)
			if (a[j] == j) pos = j;
		if (pos == 0) {
			puts("-1");
			return 0;
		}
		ans[i] = pos;
		for (int j = pos; j < i; j++)
			a[j] = a[j + 1];
	}
	for (int i = 1; i <= n; i++)
		writeln(ans[i]);
	return 0;
}

【B】 Balanced Neighbors

【思路要点】

• 考虑构成一张完全图，再删去若干条边使其合法。
• 若 $N$ 为奇数，可以删去边 $1-(N-1),2-(N-2)...$ 。
• 若 $N$ 为偶数，可以删去边 $1-N,2-(N-1)...$ 。
• 不难发现剩余的图一定也是连通的。
• 时间复杂度 $O(N^2)$ 。

【代码】

#include
using namespace std;
const int MAXN = 2e5 + 5;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int n; vector <pair <int, int>> a;
int main() {
	read(n);
	for (int i = 1; i <= n; i++)
	for (int j = i + 1; j <= n; j++)
		if (i + j != n + (n + 1) % 2) a.emplace_back(i, j);
	writeln(a.size());
	for (auto x : a)
		printf("%d %d\n", x.first, x.second);
	return 0;
}

【C】 Three Circuits

【思路要点】

• 首先，若这张图不是一张欧拉图，答案为 $No$ ，下令各点度数为偶数。
• 若存在一个点度数 $\ge 6$ ，该点将在欧拉回路上出现至少 $3$ 次，我们可以将该欧拉回路分成 $3$ 部分，答案为 $Yes$ ，下令各点度数 $\in \{2,4\}$ ，记度为 $4$ 的点数为 $cn{t}_4$ 。
• 若 $cn{t}_4\ge 3$ ，取三个度为 $4$ 的点 $A,B,C$ ，由于 $A$ 点将在欧拉回路上出现 $2$ 次，我们可以将该欧拉回路分成 $2$ 部分， $B,C$ 都会出现在某一条上 $2$ 次 $(1)$ ，或在两条上各出现 $1$ 次 $(2)$ 。对于情况 $(1)$ ，直接将对应部分的欧拉回路断开即可将原图的欧拉回路分成 $3$ 部分；对于情况 $(2)$ ， $(A,B),(B,C),(A,C)$ 间的边可分别组成 $3$ 条欧拉回路，因此答案为 $Yes$ ，下令 $cn{t}_4\le 2$ 。
• 由于形成 $3$ 条欧拉回路至少需要 $M\ge N+2$ ，因此 $M\le N+1$ 时答案为 $No$ ，剩余的情况即 $cn{t}_4=2$ ，令这两个度为 $4$ 的点为 $X,Y$ 。
• 若 $X,Y$ 之间有 $4$ 条路径，答案为 $No$ ，否则，即 $X,Y$ 之间有 $2$ 条路径，答案为 $Yes$ 。
• 时间复杂度 $O(N+M)$ 。

【代码】

#include
using namespace std;
const int MAXN = 2e5 + 5;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int n, m, cnt, x, y, d[MAXN];
vector <int> a[MAXN];
void dfs(int pos, int from) {
	if (pos == x && from) return;
	if (pos == y) {
		cnt++;
		return;
	}
	for (auto x : a[pos])
		if (x != from) dfs(x, pos);
}
int main() {
	read(n), read(m);
	if (m < n + 2) {
		puts("No");
		return 0;
	}
	for (int i = 1; i <= m; i++) {
		int x, y; read(x), read(y);
		d[x]++, d[y]++;
		a[x].push_back(y);
		a[y].push_back(x);
	}
	for (int i = 1; i <= n; i++)
		if (d[i] % 2) {
			puts("No");
			return 0;
		}
	x = 0, y = 0;
	for (int i = 1; i <= n; i++)
		if (d[i] > 2) {
			if (d[i] > 4) {
				puts("Yes");
				return 0;
			}
			if (x == 0) x = i;
			else if (y == 0) y = i;
			else {
				puts("Yes");
				return 0;
			}
		}
	dfs(x, 0);
	if (cnt == 4) puts("No");
	else {
		assert(cnt == 2);
		puts("Yes");
	}
	return 0;
}

【D】 Rotation Sort

【思路要点】

• 考虑旋转操作的本质，即选择一个数，花费一定代价将其插入至左侧任一位置，或花费一定代价将其插入至右侧任一位置。
• 考虑对于最终没有移动的数进行动态规划，记 $d{p}_{i,j}$ 表示考虑前 $i$ 个数，最后一个没有移动的数为 $j$ 的情况下最小的代价，分 $a_i>j$ 和 $a_i<j$ 转移即可。
• 时间复杂度 $O(N^2)$ 。

【代码】

#include
using namespace std;
const int MAXN = 5005;
const long long INF = 1e18;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
ll dp[MAXN][MAXN];
int n, f, b, a[MAXN];
int main() {
	read(n), read(f), read(b);
	for (int i = 1; i <= n; i++)
		read(a[i]);
	for (int i = 0; i <= n; i++)
	for (int j = 0; j <= n; j++)
		dp[i][j] = INF;
	dp[0][0] = 0;
	for (int i = 1; i <= n; i++)
	for (int j = 0; j <= n; j++) {
		ll tmp = dp[i - 1][j];
		if (tmp == INF) continue;
		if (a[i] > j) {
			chkmin(dp[i][j], tmp + f);
			chkmin(dp[i][a[i]], tmp);
		} else chkmin(dp[i][j], tmp + b);
	}
	ll ans = INF;
	for (int i = 0; i <= n; i++)
		chkmin(ans, dp[n][i]);
	writeln(ans);
	return 0;
}

【E】 Modulo Pairing

【思路要点】

• 首先，排序整个数列。
• 可以证明，所有解都可以调整至如下形式：存在一个分界点 $Mid$ ， $[1,Mid]$ 中的元素按照 $1-Mid,2-(Mid-1),...$ 的形式匹配，且各组的和小于 $M$ ； $[Mid+1,2\ast N]$ 中的元素按照 $(Mid+1)-(2\ast N),(Mid+2)-(2\ast N-1),...$ 的形式匹配，且各组的和不小于 $M$ 。
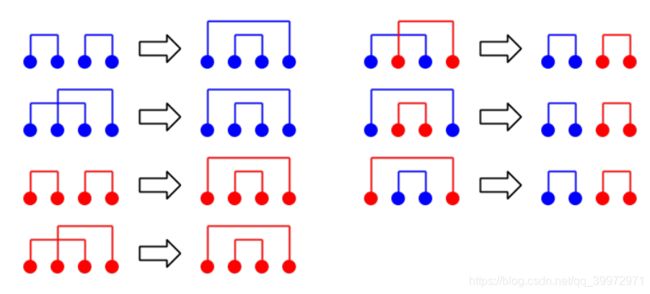
• 若用蓝线表示一组和小于 $M$ 的匹配，红线表示一组和不小于 $M$ 的匹配，按照下图的方式调整可以保证方案不会变劣。
• 
• 同时，当分界点 $Mid$ 向左移动的时候，两部分的最大和都会减少，因此，我们之需要找到使得右侧的最小和不小于 $M$ 的最小的 $Mid$ ，构造答案。二分即可。
• 时间复杂度 $O(NLogN)$ 。

【代码】

#include
using namespace std;
const int MAXN = 2e5 + 5;
const int INF = 2e9;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int n, m, a[MAXN];
bool check(int pos) {
	for (int i = 2 * pos + 1, j = 2 * n; i <= j; i++, j--)
		if (a[i] + a[j] < m) return false;
	return true;
}
int main() {
	read(n), read(m);
	for (int i = 1; i <= 2 * n; i++)
		read(a[i]);
	sort(a + 1, a + 2 * n + 1);
	int l = 0, r = n;
	while (l < r) {
		int mid = (l + r) / 2;
		if (check(mid)) r = mid;
		else l = mid + 1;
	}
	int ans = 0;
	for (int i = 1, j = 2 * l; i <= j; i++, j--)
		chkmax(ans, a[i] + a[j]);
	for (int i = 2 * l + 1, j = 2 * n; i <= j; i++, j--)
		chkmax(ans, a[i] + a[j] - m);
	writeln(ans);
	return 0;
}

【F】 One Third

【思路要点】

• 考虑将一次在 $x$ 处的划分描述为三条线，红线 $x$ ，蓝线 $x+120{}^{\circ }$ ，绿线 $x-120{}^{\circ }$ 。
• 最接近 $\frac{1}{3}$ 的值与 $\frac{1}{3}$ 的差值即为不同颜色的两条线形成的最小非负夹角。
• 令第一次划分有 $x=0$ ，在数轴上标红 $0$ ，标蓝 $\frac{1}{3}$ ，剩余的每一次划分在 $[0,\frac{1}{3})$ 内都存在恰好一个随机分布，随机颜色的点，距离最近的两个异色点的距离的期望即为答案。
• 这 $N-1$ 个点将 $[0,\frac{1}{3})$ 分成了 $N$ 份，考虑最小的一部分的期望长度 $E_1$ ，有
  $$E_1=\frac{1}{3}{\int }_0^{\frac{1}{N}}P(Len\ge x)dx=\frac{1}{3}{\int }_0^{\frac{1}{N}}(1-nx{)}^{n-1}dx=\frac{1}{3N^2}$$
• 考虑第 $i$ 小的一部分的期望长度与第 $i-1$ 小的一部分的期望长度的差 $E_i-E_{i-1}$ ，考虑将所有长度第 $j(j>i-1)$ 小的部分的长度减去第 $i-1$ 小的长度，计算剩余线段的期望最短长度，有
  $$E_i-E_{i-1}=\frac{1}{3}\times \frac{1-{\sum }_{j=1}^{i-1}(N-j+1)(E_j-E_{j-1})}{(N-i+1{)}^2}=\frac{1}{3N(N-i+1)}$$
• 每一部分都有 $\frac{1}{3}$ 的概率两端同色，因此答案 $Eans$ 有
  $$Eans=\sum _{i=1}^N\frac{1}{3^{i-1}}\times (E_i-E_{i-1})=\sum _{i=1}^N\frac{1}{3^{i}N(N-i+1)}$$
• 时间复杂度 $O(N)$ 。

【代码】

#include
using namespace std;
const int MAXN = 1e6 + 5;
const int P = 1e9 + 7;
const int inv3 = (P + 1) / 3;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int inv[MAXN];
int main() {
	int ans = 0, n;
	read(n), inv[1] = 1;
	for (int i = 2; i <= n; i++)
		inv[i] = (P - 1ll * (P / i) * inv[P % i] % P) % P;
	for (int i = 1, mul = inv3; i <= n; i++, mul = 1ll * mul * inv3 % P)
		ans = (ans + 1ll * inv[n] * inv[n - i + 1] % P * mul) % P;
	writeln(ans);
	return 0;
}