机器学习“傻瓜式”理解（5）线性回归（简单+评估+多元）

1.基础理解：

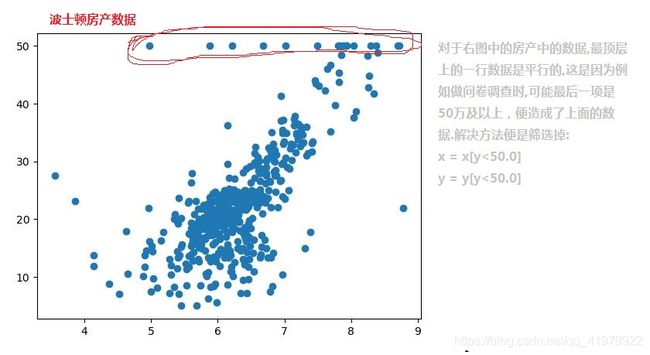
先来讲解简单线性回归，通过一张图基础理解一下：

通过对上图的理解我们可以简单概括一下简单线性回归：
只有一个特征，在多个数据集中我们尽可能的寻找一条直线能够最大程度的拟合这些数据，正如图片中所示，我们寻找除了一个目标函数，也就是损失函数，来最小化我们预测值与真实值之间的误差。
总结线性回归的特点可得到：
①线性回归如其名，主要用于解决回归问题，并且它是许多非线性回归模型的基础。
②线性回归模型的实现与推导背后有大量的数学做支撑，计算机实现较为简单。
③线性回归模型最终得出的预测结果具有很强的解释性。
下面明确参数a与b的公式推导过程：

求b:

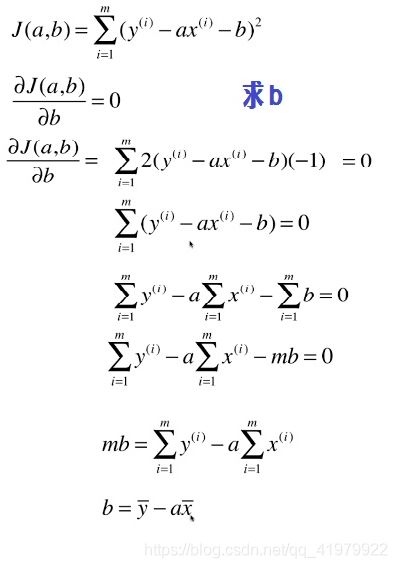
求解a:
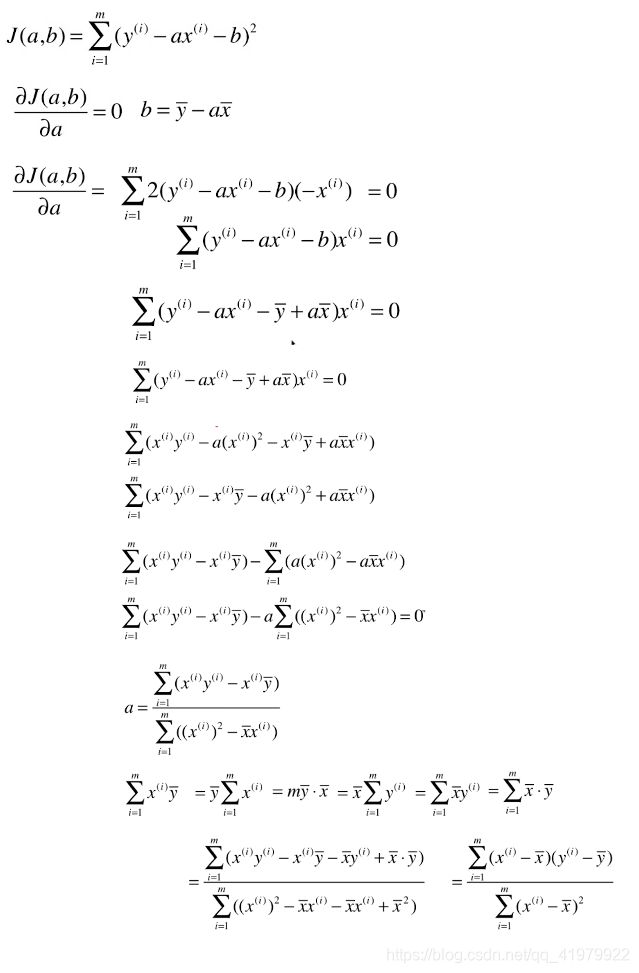封装简单线性回归:

import numpy as np
'''value the model precision'''
from sklearn.metrics import r2_score

class SimpleLinearRegression:
    def __init__(self):
        self.a_ = None
        self.b_ = None

    def fit(self,X_train,y_train):
        '''check'''
        assert X_train.ndim == 1,"the dimension must be 1"
        assert len(X_train)== len(y_train),\
                "the size must be valid"

        x_mean = np.mean(X_train)
        y_mean = np.mean(y_train)

        self.a_ = ((X_train - x_mean).dot(y_train - y_mean)) / ((X_train - x_mean).dot(X_train - x_mean))
        self.b_ = y_mean - (self.a_ * x_mean)

        return self

    def predict(self,X_test):
        '''check'''
        assert self.a_ is not None and self.b_ is not None,\
                "predict after fit"
        assert X_test.ndim == 1,"the dimension must be 1"

        return np.array([self._predict(x) for x in X_test])

    def _predict(self,x):
        return self.a_ * x + self.b_

    def score(self,X_test,y_test):
        y_predict = self(X_test)
        return r2_score(y_test,y_predict)

    def __repr__(self):
        return "SimpleLinearRegression()"

简单总结一下线性回归
①线性回归与KNN算法内部实现原理不同，很明显线性回归算法用于解决回归问题，而且是一种参数学习算法，不过度的依赖数据，通常情况下，线性回归算法在学习到参数以后就可以舍弃训练数据集了。
②线性回归算法是其他众多非线性回归算法的基础，并且线性回归算法具有很强的假设性以及解释性（这一点我们将在后面详细阐明），而且重要的一点是，只需要稍微的改变一点线性回归算法就可以灵活的解决非线型问题。
③不好的一点是算法的时间复杂度十分高：O(n3)（即使优化后O(n2.4)）

线性回归算法的解释性（波士顿房价预测为例）

代码实现：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LinearRegression

boston = datasets.load_boston()
X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]

lin_model = LinearRegression()
lin_model.fit(X,y)

'''
参数解释：
lin_model.coef_:存储了多元项中每一个系数
lin_model.feature_names:存储的特征名
'''

'''对系数排序后返回的index对特征进行排序'''
result = boston.feature_names[np.argsort(lin_model.coef_)]

print(result)

从上面得到的结果便可以看出来，每一个系数对应的特征名都可以说明一个数据。
例如，“RM”表示房间数量，系数最大，说明房屋数量越多，房价越高。而“NOX”表示房间周围一氧化碳的浓度，系数最小，表示其对房价的影响很小，这便是线性回归解释性的重要体现。

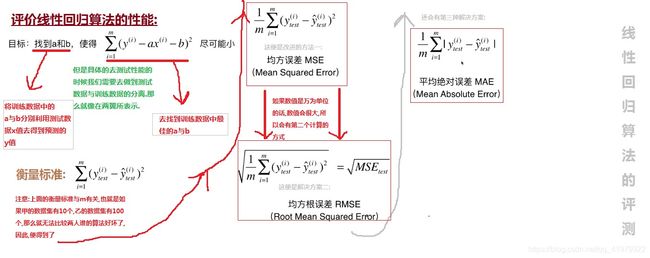
2.评价性能

按照惯例，我们还是使用一张图片先来解释三个基础的衡量算法：

再来一张：

sklearn中在metrics中封装了四种衡量方式的计算方法，为了更好的理解公式，我们进行封装。

import numpy as np
from math import sqrt

def accuracy_score(y_true,y_predict):
    '''check'''
    assert y_true.shape[0] == y_predict.shape[0],\
            "the size must be valid"
    return int((np.sum(y_true == y_predict) / len(y_true)) * 100)

def mean_squared_error(y_true,y_predict):
    '''check'''
    assert len(y_true) == len(y_predict),\
            "the size must be valid"
    return np.sum((y_true - y_predict)**2) / len(y_true)

def root_mean_squared_error(y_true,y_predict):
    return sqrt(mean_squared_error(y_true,y_predict))

def mean_absolute_error(y_true,y_predict):
    '''check'''
    assert len(y_true) == len(y_predict), \
        "the size must be valid"
    return np.sum(np.absolute(y_true - y_predict)) / len(y_true)

def r2_score(y_true,y_predict):
    return 1 - mean_absolute_error(y_true,y_predict) / np.var(y_true)

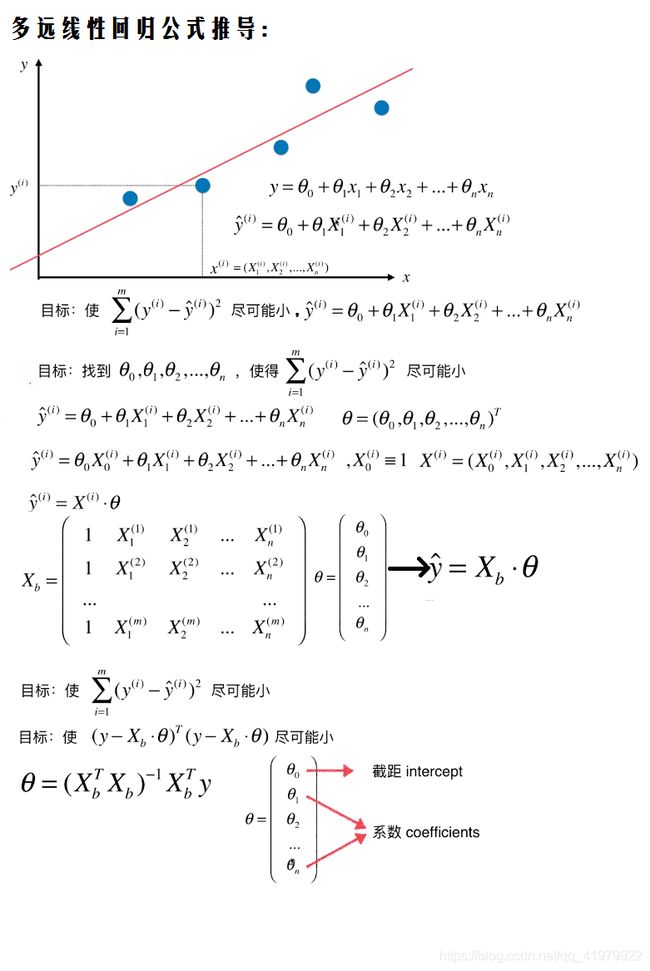
3.多元线性回归

提示:后面会讲到多项式回归算法，后面会解释多元线性回归和多项式回归的区别
要点理解:
①简单线性回归解决的是只有一个特征的问题，而多元线性回归如其名解决的是多维特征的问题。
②多元特征中每一个特征都跟y呈线性关系，但是系数有大小正负，就像上面所列举的波士顿房产价格预测案例所指。
③多元线性回归可以解决一元的问题。

多远线性回归问题解决思路:

实现代码封装:

class LinearRegression:
    def __init__(self):
        self._theta = None
        self.interception_ = None
        self.coef_ = None

    def fit_normal(self,X_train,y_train):
        '''check'''
        assert X_train.shape[0] == y_train.shape[0],\
                "the size must be valid"

        X_b = np.hstack([np.ones((len(X_train),1)),X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
        self.coef_ = self._theta[1:]
        self.interception_ = self._theta[0]
        return self

    def predict(self,X_predict):
        '''check'''
        assert self.interception_ is not None and self.coef_ is not None,\
                "fit before predict"
        assert X_predict.shape[1] = len(self.coef_),\
                "the size must be valid"

        X_b = np.hstack([np.ones((len(X_predict),1)),X_predict])
        return X_b.dot(self._theta)

    def score(self,X_test,y_test):
        y_predict = self.predict(X_test)
        return r2_score(y_test,y_predict)

    def __repr__(self):
        return "LinearRegression()"