深度学习各类优化器详解（动量、NAG、adam、Adagrad、adadelta、RMSprop、adaMax、Nadam、AMSGrad）

深度学习梯度更新各类优化器详细介绍

  这篇文章将按照时间线详细讲解各类深度学习优化器，包括常用与不常用的，为这篇博客的个人笔记，但是本文将对每个优化器进行更加清晰的讲解，添加了很多我个人理解补充，所以可以更容易理解每一个优化器，对于深度学习小白来说也可以很容易看懂。

一、前言：

  最新的深度学习库包含各种优化梯度下降的算法，比如有caffe、keras、tensorflow、pytorch等，但是通常这些算法被当做一个黑匣子使用，所以无法比较这些算法的优与劣。

二、梯度下降变形形式

1、批量归一化（BGD）

  每次经过完整一轮训练后更新一次参数，这使得梯度下降过程变得比较慢，并且需要很大内存保存中间结果。
代码表示：

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params =params - learning_rate * params_grad

2、随机梯度下降（SGD）

  随机梯度下降是对每个训练样本就更新一次网络参数，这样使得网络更新参数速度很快，但是问题就是由于训练数据多样，容易朝偏离网络最优点方向训练，网络训练不稳定。
代码表示：

for i in range(nb_epochs):
    np.random.shuffle(data)
    for example in data:
        params_grad= evaluate_gradient(loss_function, example, params)
        params =params - learning_rate * params_grad

3、小批量梯度下降（MBGD）

  小批量梯度下降是批量梯度下降与随机梯度下降之间的一个折中，即经过一个小批量的训练数据更新一次参数，可以保证网络训练速度不太慢，也能使训练方向不至于偏离太多，具有一定稳定性。当使用小批量梯度下降时，通常也使用SGD这个术语。
代码表示：

for i in range(nb_epochs):
    np.random.shuffle(data)
    for batch in get_batches(data, batch_size=50):
        params_grad= evaluate_gradient(loss_function, batch, params)
        params =params - learning_rate * params_grad

三、梯度下降遇到的困难

  小小批量梯度下降不仅不能保证良好的收敛性，而且也存在一些其他的问题：
（1）很难选择一个合适的学习率，如果学习率太小，将会导致收敛非常缓慢；如果学习率太大，也会阻碍收敛，导致损失函数值在最小值附近波动甚至发散。
（2）上述问题可以通过提前定义一个学习速率表，当达到相应轮数或者阈值时根据表改变学习率，但是这样无法适应训练数据本身特征。
（3）并且，对于所有参数我们使用同一个学习速率，如果我们的数据是稀疏的或者我们特征具有不同的频率，我们可能不希望将它们更新到同样的程度，并且我们希望对那些出现频率低的特征更新更快。
（4）另外在神经网络中，普遍是具有非凸的误差函数，这使得在优化网络过程中，很容易陷入无数的局部最优点，而且更大困难往往也不是陷入局部最优点，而是来自鞍点（也就是在一个维度上其梯度是递增，另一个维度其梯度是递减，而在鞍点处其梯度为0），这些鞍点附近往往被相同误差点所包围，且在任意维度梯度近似为0，所以随机梯度下降很难从这些鞍点逃出。如下图：

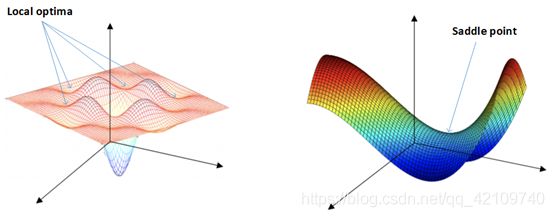
四、梯度下降优化算法

  接下来将列举一些被深度学习社区广泛用于解决上述困难的算法，这些算法有个共同之处，一般是求一阶动量(m)和二阶动量(V)，然后利用一阶、二阶动量本身或者他们组合来优化梯度下降（其中一阶动量为与梯度相关函数，二阶动量为与梯度平方相关的函数）
  首先还是给出梯度下降的公式：
  引入梯度下降优化算法后：

1、动量（momentum）

  随机梯度下降的方法很难通过峡谷区域（也就是在一个维度梯度变化很大，另一个维度变化较小），这个很好理解，因为梯度下降是梯度更新最大的反方向，如果这个时候一个维度梯度变化很大，那么就很容易在这个方向上振荡，另一个方向就更新很慢，如下图：


  上面上图没有加动量，下图加了动量的方法，可以看到有动量可以在变化小的维度上加快更新，使得加快收敛。该方法是通过添加一个参数β构建一个一阶动量m,其中m有下列表达式：

  而对于其二阶动量V=1，所以其参数更新公式为：
  其中β一般取0.9，接下来我不会立即来讲解上面两个公式为什么是这样，怎么理解。我们来看看其它表达式，相信大家在搜索动量梯度下降时，有时候在其它地方也会看到下面这种表达式：

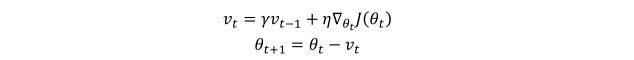
  这里的γ一般也是等于0.9，看起来这两种表达式有很大不一样，其实是差不多的，只不过第一种我觉得看起来更容易理解，第二种我觉得就不是那么明显的去理解，下面我将根据这两种表达式对比并分析动量梯度下降原理，这样更容易理解，将表达式继续拆开可以得到：

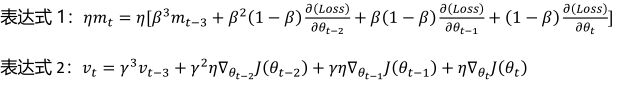
  从上述表达式可以看出，对于公式1，m(t)其实就是当前梯度的（1-β）倍，加上上一次梯度的β（1-β）倍，一直以β倍向前加，从公式中可以看到，所有项的系数加起来其实是等于1的"(1-β)+β(1-β)+β²(1-β)+β³=1";而对于表达式2，我们可以看到v(t)等于当前η倍梯度，加上前一次η倍梯度的γ倍，一直通过γ倍向前传播，这里两个公式是一样的，但是可以注意到的是，表达式2中其系数"1+γ+γ²+γ³"却不等于1，而是直接以指数形式相加的结果，而这就是两个表达式的区别所在，该两种表达方式我从两个地方看到，表达式1为我从中国大学生mooc清华大学曹健老师的“人工智能实践：tensorflow”课程中看到，表达式2我是从论文“An overview of gradient descent optimization algorithms”看到，如果你去搜"momentum"原论文，你会发现表达式又不一样，但是我们发现他们本质还是一样的，也就是添加了一个变量β，通过β倍传递给前一次的梯度。
  至于哪个表达式更好，我觉得对于表达1，他在刚开始训练时我觉得就有难以解释，因为这个时候参数更新按理说应该等于此时lr倍梯度大小，但是却被乘一个（1-β）的系数，但是对于后期我觉得解释性就更强，因为他们系数加起来等于1，这是我们希望的结果，即此时的参数更新幅度总体还是跟现在lr倍梯度大小处于同一个等级。对于表达式2，刚开始训练就没有表达式1那个问题，但是后面就有点难解释，因为根据等比数列求和公式：

当n很大时，系数和约为10，也就是说现在他的参数更新幅度是当前梯度幅度的10倍，这就让我有点难理解了，或许这样会加快训练速度？但是我反而觉得会造成参数更新的不稳定。所以总的来说我还是觉得表达式1更合适点
  再来解释下动量梯度更新的现实意义理解，首先来看看“An overview of gradient descent optimization algorithms”这篇论文中的比喻：“从本质上说，动量法，就像我们从山上推下一个球，球在滚下来的过程中累积动量，变得越来越快（直到达到终极速度，如果有空气阻力的存在，则γ<1）。同样的事情也发生在参数的更新过程中：对于在梯度点处具有相同的方向的维度，其动量项增大，对于在梯度点处改变方向的维度，其动量项减小。因此，我们可以得到更快的收敛速度，同时可以减少摇摆。”，这样解释视乎就能够解释之前表达式2的含义了，把其当做动量的累加，比如小球在下坡山坡上，那么根据表达式2，梯度方向是一直向下的，自然参数更新幅度也就是一直累加的，也就变得越来越大；而当遇到山沟，越过山沟此时就在另一边山坡，这个时候梯度方向是跟之前相反的，此时由于之前梯度大小的累加，在两个山坡间的变化就会被互相抵消掉，也就不会一直在两个山坡振荡，容易朝山沟向下走，也就是减少摇摆了。

2、NAG（Nesterov accelerated gradient）

  回顾动量的方法，我们发现参数更新是基于两部分组成，一部分为当前位置的梯度，另一部分为前面累计下来的梯度值，参数更新方向就是将两者矢量相加的方向，但是我们会发现一个问题，当刚好下降到山谷附近时，如果这个时候继续以这样的方式更新参数，我们会有一个较大的幅度越过山谷，即：模型遇到山谷不会自动减弱更新的幅度。NAG针对上述问题对动量方法进行了改进，其表达式如下，其中一阶动量项m如下，二阶动量为1。

  它是利用当前位置处先前的梯度值先做一个参数更新，然后在更新后的位置再求梯度，将此部分梯度然后跟之前累积下来的梯度值矢量相加，简单的说就是先根据之前累积的梯度方向模拟下一步参数更新后的值，然后将模拟后的位置处梯度替换动量方法中的当前位置梯度。为什么解决了之前说的那个问题呢？因为现在有一个预测后一步位置梯度的步骤，所以当在山谷附近时，预测到会跨过山谷时，该项梯度就会对之前梯度有个修正，相当于阻止了其跨度太大。下面这张图对其有个形象描述，其中蓝色线表示动量方法，蓝色短线表示当前位置梯度更新，蓝色长线表示之前累积的梯度；第一个红色线表示用NAG算法预测下一步位置的梯度更新，第一条棕色线表示先前累积的梯度，其矢量相加结果（绿色线）就是参数更新的方向。

3、Adagrad

  之前提到过这个问题：对于所有特征，我们的学习率一直没有变。怎么理解呢？假设我们用一批数据训练网络，这个数据中只有少部分数据含有某个特征，另一个特征几乎全部数据都具有，当这些数据通过训练时，对于不同特征我们假设对应于不同的神经元权重，对于都含有的特征，这些神经元对应参数更新很快，但是对于那些只有少部分数据含有的特征，对应神经元权重获得更新机会就少，但是由于学习率一样，这样可能导致神经网络训练的不充分。
  adagrad算法就是为了解决这个问题，让学习率学习数据的特征自动调整其大小，adagrad算法引入了二阶动量，其表达式为：

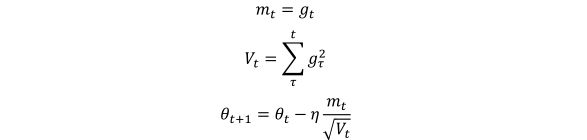
  其中g(t)为t时刻参数梯度，下面来讲解为什么adagrad可以实现不同频率特征对其参数学习率改变，首先，我们看到二阶动量V(t)，它是梯度平方累加和，对于训练数据少的特征，自然对应的参数更新就缓慢，也就是说他们的梯度变化平方累加和就会比较小，所以对应于上面参数更新方程中的学习速率就会变大，所以对于某个特征数据集少，相应参数更新速度就快。为了防止上述分母为0，所以往往添加一个平滑项参数ε，参数更新方程也就变成：

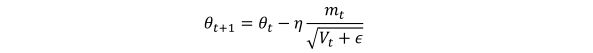
  但是adagrad同样也有问题，就是其分母随着训练数增加，也会跟着增加，这样会导致学习速率越来越小，最终变的无限小，从而无法有效更新参数。

4、adadelta

  adadelta算法可以解决上述问题，其一阶向量跟adagrad一样，二阶参数有所变化：

  可以看到其二阶参数表达式跟动量的表达式类似，引入了参数γ，可以知道二阶动量其实之前所有梯度平方的一个加权均值，表达式如下：

  所以，对于adagrad算法带来的分母越来越大的问题就可以解决了。但是作者注意到，此算法以及之前提到的算法（SGD、动量、adagrad）的参数之间单位并不匹配，而按理说参数更新应该具有与参数相同的单位。怎么理解这点呢？让我们来对随机梯度下降算法（SGD）来进行参数之间单位关系讨论，我们知道，SGD算法的参数更新方程式为：

假设loss的单位为b，而参数的单位为c，学习率没有单位，设为1，这个时候我们就发现，上面的等式的单位运算为：c=c-1*(b/c)，这明显单位不匹配，这就是作者说的问题（我觉得这个作者很强，这点真的很巧妙，我估计作者是物理专业方向的，物理就经常讨论单位变换）。
  作者这里又提出一个很巧妙的解决方法，那就是利用与二阶动量V(t)类似的运算对参数变化量deta(θ)做运算求它的二阶动量:

这里将上述运算用一个新符号RMS[X]表示，即对梯度的二阶动量变化为RMS[g],对变量的变化量的二阶动量为RMS[deta(θ)]，然后将其替换学习率，最后梯度更新公式为：

  我们可以验证一下，现在方程中参数单位是否会匹配，其中参数单位还是为c，loss单位为b，方程参数的单位运算有：c=c-[c/(b/c)]b/c;显而易见单位是匹配的。通过adadelta算法，我们甚至可以不需要设置一个默认的学习率，因为在新的规则中已经移除了这项。

5、RMSprop

  RMSprop算法由hinton教授提出，它与adadelta算法公式其实是一样的，他们是在相同时间被独立的提出，公式自然也为：

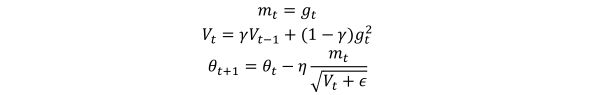
hinton教授建议将γ设置为0.9，对于学习率，一个好的固定值为0.001。

6、Adam

  Adam(Adaptive Moment Estimation)自适应矩估计，是另一种自适应学习率的算法，它是一种将动量和Adadelta或RMSprop结合起来的算法，也就引入了两个参数β1和β2，其一阶和二阶动量公式为：

  作者发现一阶和二阶动量初始训练时很小，接近为0，因为β值很大，于是作者重新计算一个偏差来校正：

  其中t代表其t次方，所以刚开始训练时，通过除于（1-β）就可以很好修正学习速率，当训练多轮时，分母部分也接近1，又回到了原始方程，所以最后总的梯度更新方程为：

  其中β1默认值为0.9，β2默认值为0.999,ε为10^-8，Adam集合动量和Adadelta两者的优点，从经验中表明Adam在实际中表现很好，同时与其他自适应学习算法相比，更有优势。

7、AdaMax

  adam更新规则中的系数与过去梯度V(t-1)和现在梯度g(t)²的L2范数成反比

作者提出是否可以考虑其他的Lp范数，也就是扩展到p阶动量，有方程式：

  通常大的p值会造成数字不稳定，所以一般常用的都是L1和L2范数，但是L∞通常也可以有比较稳定的结果，所以作者引入了无穷阶的动量，对应于梯度更新的分母项用字母u代替，也就是：

  将u变换下可能更好理解：

  可以看到u不会为0，所以也就不需要如adam一样，分母还需要添加一个ε，通常默认参数大小为：

8、Nadam

  Adam将RMSprop和动量结合起来，我们也可以看到NAG其实比动量表现更好。
Nadam（Nesterov-accelerated Adaptive
Moment Estimation），Nesterov加速的自适应矩估计，将adam和NAG结合起来，为了将NAG添加到Adam，我们需要对动量部分进行一些改变。作者将NAG梯度更新公式变为：

  也就是现在不再像NAG提前预测后面位置，而是直接在当前位置对当前梯度方向做两次更新，同样运用到Adam中需要对m做一个修正：

  最后得到Nadam梯度更新方程为：

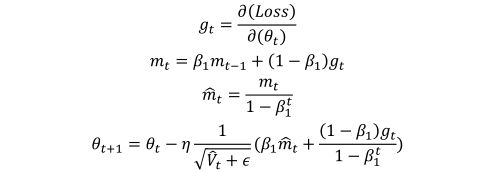
9、AMSGrad

  随着自适应学习速率的方法成为训练神经网络的规范，研究者就发现，在一些情况下比如目标识别、机器翻译领域，自适应学习速率的方法无法收敛到最佳情况，并且弱于基于动量的随机梯度下降。
其梯度更新公式为：

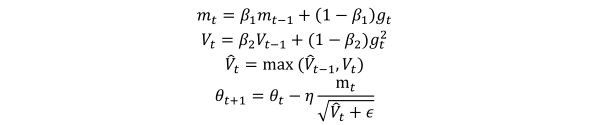
10、目前其它的优化器

  在AMSGrad后，有很多其它的优化器出现，包括AdamW，修复adam的权重下降问题；QHAdam，用基于动量的随机梯度下降平均标准的随机梯度下降；AggMo，结合多个动量项；等其他优化器。

五、可视化优化器

六、优化SGD的其他策略

1、Shuffling and Curriculum Learning

2、Batch normalization

3、Early stopping

4、Gradient noise

  具体分析请关注我的博客，后续再单独出几篇文章介绍。

总结

  以上就是我今日笔记，笔记已经整理成word文档，word文档包括各类公式的原版，因为csdn上输入公式很麻烦所以都统一输入图片格式，想要原版的可以点击此处下载。