机器学习(七)线性回归与岭回归Lasso回归与弹性网络与正则化
机器学习(七)
线性回归
最小二乘法(Least Squares Method,简记为LSE)是一个比较古老的方法,源于天文学和测地学上的应用需要。在早期数理统计方法的发展中,这两门科学起了很大的作用。丹麦统计学家霍尔把它们称为“数理统计学的母亲”。此后近三百年来,它广泛应用于科学实验与工程技术中。美国统计史学家斯蒂格勒( S. M. Stigler)指出, 最小二乘方法是19世纪数理统计学的压倒一切的主题。1815年时,这方法已成为法国、意大利和普鲁士在天文和测地学中的标准工具,到1825年时已在英国普遍使用。追溯到1801年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星。高斯于其1809年的著作《关于绕日行星运动的理论》中。在此书中声称他自1799年以来就使用最小二乘方法,由此爆发了一场与勒让德的优先权之争。近代学者经过对原始文献的研究,认为两人可能是独立发明了这个方法,但首先见于书面形式的,以勒让德为早。然而,现今教科书和著作中,多把这个发明权归功于高斯。其原因,除了高斯有更大的名气外,主要可能是因为其正态误差理论对这个方法的重要意义。勒让德在其著作中,对最小二乘方法的优点有所阐述。然而,缺少误差分析。我们不知道,使用这个方法引起的误差如何,就需建立一种误差分析理论。高斯于1823年在误差e1 ,… , en独立同分布的假定下,证明了最小二乘方法的一个最优性质: 在所有无偏的线性估计类中,最小二乘方法是其中方差最小的!在德国10马克的钞票上有高斯像,并配了一条正态曲线。在高斯众多伟大的数学成就中挑选了这一条,亦可见这一成就对世界文明的影响。
最小二乘法


线性 : 得名于f(x)=ax+b的图像的形象 很直观 就是一条直线的形象

梯度下降:

-------------------------------------------------------------------------------------------------------------------------------------------------
岭回归
岭回归优点:
1.缩减方法可以去掉不重要的参数,因此能更好地理解数据。此外,与简单的线性回归相比,缩减法能取得更好的预测效果。
2.岭回归是加了二阶正则项的最小二乘,主要适用于过拟合严重或各变量之间存在多重共线性的时候,岭回归是有bias的,这里的bias是为了让variance更小。
过拟合:为了得到一致假设而使假设变得过度严格称为过拟合
bias:bias:指的是模型在样本上的输出与真实值的误差
variance:指的是每个模型的输出结果与所有模型平均值(期望)之间的误差
总结:
1.岭回归可以解决特征数量比样本数量多的问题
2.岭回归作为一种缩减算法可以判断哪些特征重要或者不重要,类似于降维效果
3.缩减算法可以看作是对一个模型增加偏差的同时减小方差
应用场景:
1.数据点少于变量个数
2.变量间存在共线性(最小二乘法得到的系数不稳定,方差很大)
多重共线性(Multicollinearity)是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确
3.处理高度相关的数据
拓展:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
###############################################################################
# Compute paths
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
clf = linear_model.Ridge(fit_intercept=False)
coefs = []
for a in alphas:
clf.set_params(alpha=a)
clf.fit(X, y)
coefs.append(clf.coef_)
###############################################################################
# Display results
plt.figure(figsize=(12,9))
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()
效果:

-------------------------------------------------------------------------------------------------------------------------------------------------
Lasso回归(least absolute shrinkage and selection operator,最小绝对值收缩和选择算子)
简介:
与岭回归类似,它也是通过增加惩罚函数来判断、消除特征间的共线性。

当λ足够小时,一些影响较弱的系数会因此被迫缩减到0
-------------------------------------------------------------------------------------------------------------------------------------------------
弹性网络ElasticNet
ElasticNet综合了L1正则化项和L2正则化项
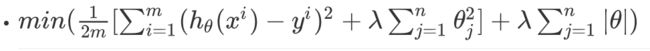
使用场景:
ElasticNet在我们发现用Lasso回归太过(太多特征被稀疏为0),而岭回归也正则化的不够(回归系数衰减太慢)的时候,可以考虑使用ElasticNet回归来综合,得到比较好的结果。
-------------------------------------------------------------------------------------------------------------------------------------------------
正则化
作用:
机器学习中,如果参数过多,模型过于复杂,容易造成过拟合(overfit)。即模型在训练样本数据上表现的很好,但在实际测试样本上表现的较差,不具备良好的泛化能力。为了避免过拟合,最常用的一种方法是使用使用正则化,例如 L1 和 L2 正则化

L1正则化:
即原损失函数 + 所有权重的平均绝对值 * λ ,其中λ >0
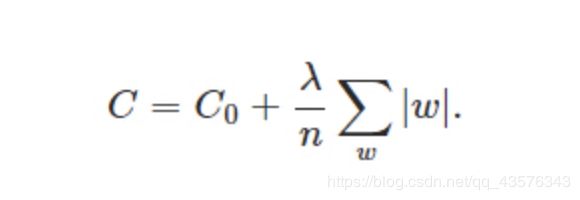

表达式中sgn(w)表示w的符号。那么权重w的更新规则为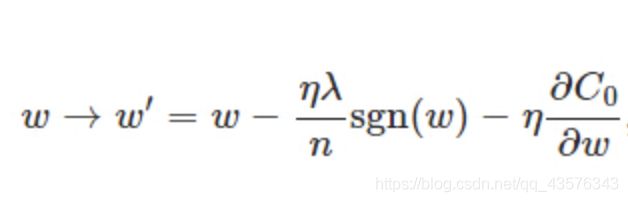
η(/'i:tə/)是学习率,就是步幅的意思
L2正则化:
即原损失函数 + 所有权重平方和的平均值 * λ / 2 , λ>=0
总结:
比原始的更新规则多出了η * λ * sgn(w)/n这一项。当w为正时,更新后的w变小。当w为负时,更新后的w变大——因此它的效果就是让w往0靠,使网络中的权重尽可能为0,也就相当于减小了网络复杂度,防止过拟合。

