sklearn降维2: 主成分分析PCA原理python过程

import numpy as np
import pandas as pd
df = pd.read_csv('iris.data')
df.columns = ['sepal_len','sepal_wid','petal_len','petal_wid','class']
df.head()

X = df.iloc[:,0:4].values
y = df.iloc[:,4].values

import matplotlib.pyplot as plt
import math

label_dict = {1:'Iris-Setosa', 2:'Iris-Versicolor', 3:'Iris-Virgnica'}
feature_dict = {0:'sepal length', 1:'sepal width', 2:'petal length', 3:'petal width'}

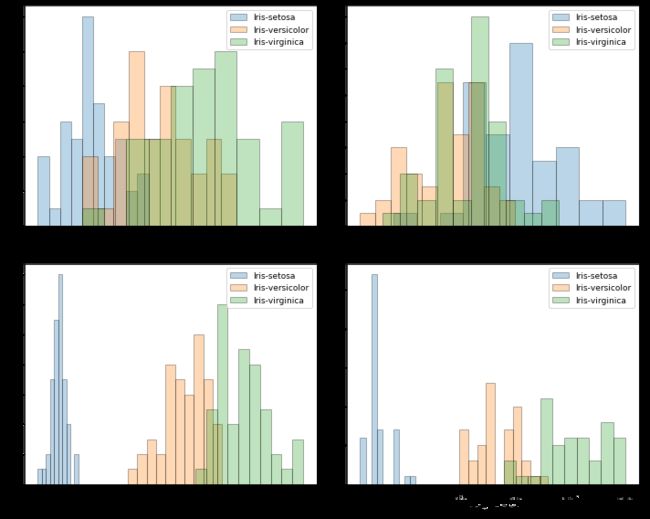
plt.figure(figsize = (10, 8))
for cnt in range(4):
    plt.subplot(2, 2, cnt+1)
    for lab in ('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'):
        plt.hist(X[y==lab, cnt], label=lab, bins=10, alpha=0.3, edgecolor='black')
    plt.xlabel(feature_dict[cnt])
    plt.legend(loc = 'upper right', fancybox = True, fontsize = 9)
plt.tight_layout();
plt.show()

from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)

mean_vec = np.mean(X_std, axis=0)
cov_mat = (X_std - mean_vec).T.dot(X_std - mean_vec) / (X_std.shape[0] - 1) #协方差矩阵
print('Covariance matrix \n%s' % cov_mat)

# print('Numpy covariance matrix:\n%s' % np.cov(X_std.T)) # numpy库中的协方差矩阵

Covariance matrix
[[ 1.00675676 -0.10448539 0.87716999 0.82249094]
[-0.10448539 1.00675676 -0.41802325 -0.35310295]
[ 0.87716999 -0.41802325 1.00675676 0.96881642]
[ 0.82249094 -0.35310295 0.96881642 1.00675676]]

eig_vals, eig_vecs = np.linalg.eig(cov_mat) #特征值,特征向量
print('Eigenvectors(特征向量) \n%s' % eig_vecs)
print('Eigenvalues(特征值) \n%s' % eig_vals)

Eigenvectors(特征向量)
[[ 0.52308496 -0.36956962 -0.72154279 0.26301409]
[-0.25956935 -0.92681168 0.2411952 -0.12437342]
[ 0.58184289 -0.01912775 0.13962963 -0.80099722]
[ 0.56609604 -0.06381646 0.63380158 0.52321917]]
Eigenvalues(特征值)
[2.92442837 0.93215233 0.14946373 0.02098259]

eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
eig_pairs.sort(key = lambda x:x[0], reverse = True)
print('Eigenvalues in descending order:')
for i in eig_pairs:
    print(i[0])

Eigenvalues in descending order:
2.924428369111114
0.9321523302535073
0.1494637348981338
0.02098259276427051

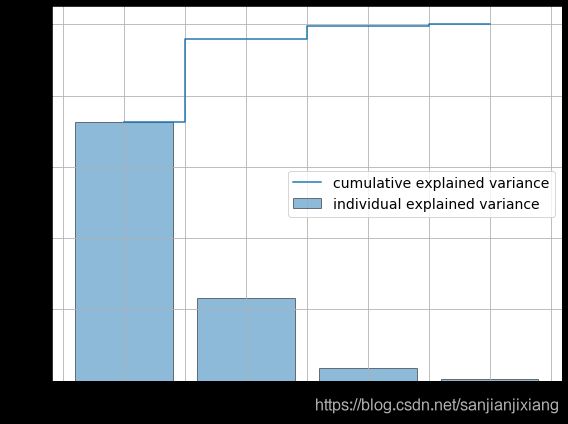
tot = sum(eig_vals)
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]

cum_var_exp = np.cumsum(var_exp) # 累加和
print(cum_var_exp)

plt.figure(figsize = (8, 6))
plt.bar(range(4), var_exp, alpha=.5, align='center', edgecolor='k', label='individual explained variance')
plt.step(range(4), cum_var_exp, where='mid', label = 'cumulative explained variance')
plt.ylabel('Explained variance ratio', fontsize = 15)
plt.xlabel('Principal components', fontsize = 15)
plt.legend(loc = 'best', fontsize = 14)
plt.grid()
plt.tight_layout()
plt.show()

[ 72.62003333 95.76744019 99.47895575 100. ]

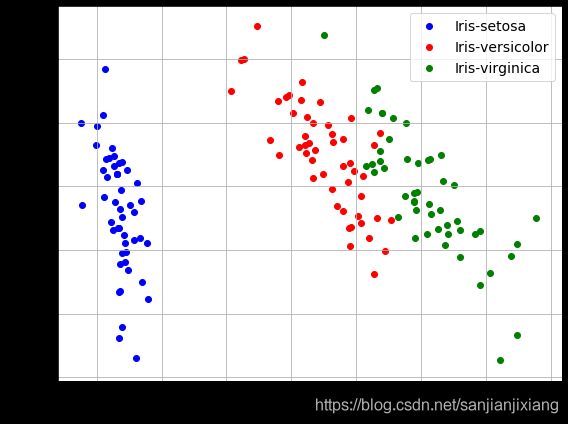
# 原始数据画图
plt.figure(figsize = (8,6))
for lab,col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),('b','r','g')):
    plt.scatter(X[y==lab,0],X[y==lab,1], label=lab, c=col)
plt.xlabel('sepal_len', fontsize=15)
plt.ylabel('sepal_wid', fontsize=15)
plt.legend(loc = 'best', fontsize=14)
plt.tight_layout()
plt.grid()
plt.show()

#python主成分分析后画图
matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1), eig_pairs[1][1].reshape(4,1)))
Y = X_std.dot(matrix_w)

plt.figure(figsize = (8, 6))
for lab,col in zip(('Iris-setosa','Iris-versicolor','Iris-virginica'),('b','r','g')):
    plt.scatter(Y[y==lab,0],Y[y==lab,1], label=lab, c=col)
plt.xlabel('Principal Component 1', fontsize=15)
plt.ylabel('Principal Component 2', fontsize=15)
plt.tight_layout()
plt.legend(loc = 'best', fontsize=14)
plt.grid()
plt.show()

sklearn中PCA模块

# 原数据直接PCA后画图
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X_pca = pca.fit_transform(X)

plt.figure(figsize = (8, 6))
for lab,col in zip(('Iris-setosa','Iris-versicolor','Iris-virginica'),('b','r','g')):
    plt.scatter(X_pca[y==lab,0],X_pca[y==lab,1]*-1,label=lab,c=col)
plt.xlabel('Principal Component 1', fontsize=15)
plt.ylabel('Principal Component 2', fontsize=15)
plt.legend(loc = 'best', fontsize=14)
plt.tight_layout()
plt.grid()
plt.show()

# 数据标准化后PCA画图
pca = PCA(n_components = 2)
X_std_pca = pca.fit_transform(X_std)

plt.figure(figsize = (8, 6))
for lab,col in zip(('Iris-setosa','Iris-versicolor','Iris-virginica'),('b','r','g')):
    plt.scatter(X_std_pca[y==lab,0],X_std_pca[y==lab,1]*-1,label=lab,c=col)
plt.xlabel('Principal Component 1', fontsize=15)
plt.ylabel('Principal Component 2', fontsize=15)
plt.legend(loc = 'best', fontsize=14)
plt.tight_layout()
plt.grid()
plt.show()