Andrew Ng 深度学习课程——卷积神经网络(CNN)
主要是记录网易云课堂上的网络课卷积神经网络的笔记
| date | version | comments |
|---|---|---|
| 2019/9/3 | V0.1 | Init |
文章目录
- 卷积神经网络
- 边缘检测
- padding, stride
- 三通道(RGB)图片的卷积
- 单层CNN
- 其他概念
- CNN网络
- 代码实现
- 深度卷积网络:实例探究
- LeNet-5
- AlexNet
- VGG-16
- ResNet
- Inception(GooLeNet)
- 迁移学习
- 数据增广(Data augmentation)
- 目标检测(Object detection)——YOLO算法
- 目标定位
- 滑动窗口目标检测
- 使用卷积的滑动窗口目标检测
- bounding box预测
- 交并比
- 非极大值抑制
- Anchor Boxes
- YOLO算法
- 特殊应用:人脸识别和神经风格转化
- 人脸识别场景
- Siamese network
- 三元组损失函数(Triplet loss)
- 面部特征与二分类
- 神经风格转化
- 损失函数(cost function)
卷积神经网络
在前面学习,可以实现神经网络的搭建,使用图片识别的话,是将图片RGB三个通道flatten成为一个很长的向量来处理,之前处理的图片都比较小,如果图片比较大假设1000x1000x3,第一个输出层的输出为10000,那么这一层的 W W W就是 [ 10000 , 3000000 ] [10000,3000000] [10000,3000000]维的,这样一共就有300亿个参数需要学习,这还仅仅只有一层。实现少量参数同样可以训练这么大的图片的网络结构就是卷积神经网络(Convolutional Neural Network, CNN)。
边缘检测
在计算机视觉(Computer Vision, CV)领域中,实现图片的边缘检测就是只用一个过滤器或者叫核(filter)不断迭代在图片中的某一部分,将突变比较明显的信息放大。比如检测垂直的边沿,那么使用过滤器: f i l t e r = [ 1 0 − 1 1 0 − 1 1 0 − 1 ] filter=\begin{bmatrix}1&0&-1\\1&0&-1\\1&0&-1\end{bmatrix} filter=⎣⎡111000−1−1−1⎦⎤都先在选取一张灰度图图片img[1:3,1:3]与filter对应元素相乘后求和,然后img[2:4,1:3]与filter对应元素相乘(index从1开始取)后求和,然后继续…直到选取到img[end-2:end,end-2:end],这样就把竖直方向的变化放大了。实现的过程如下图(图中的filter不是竖直方向的):
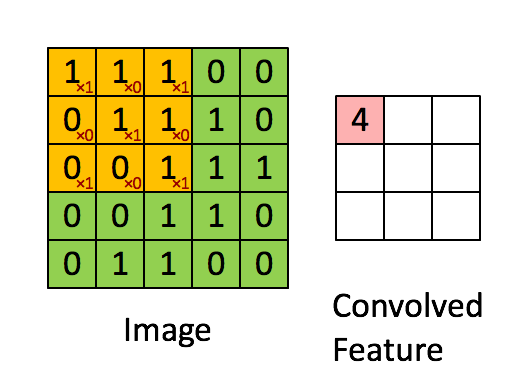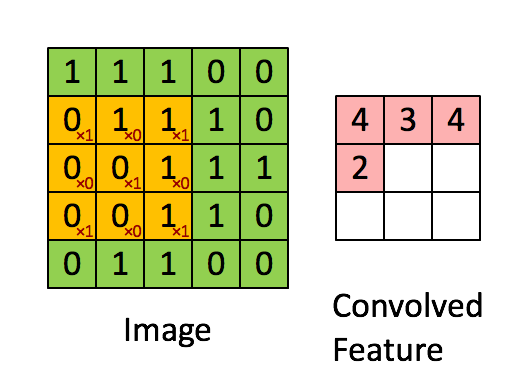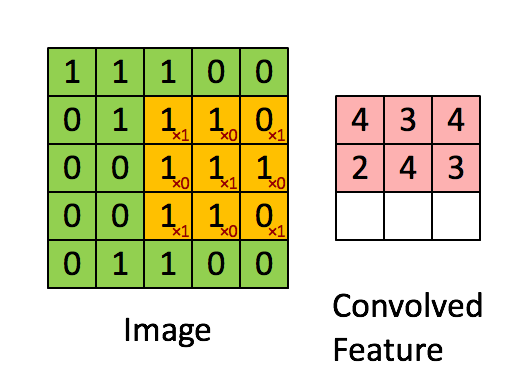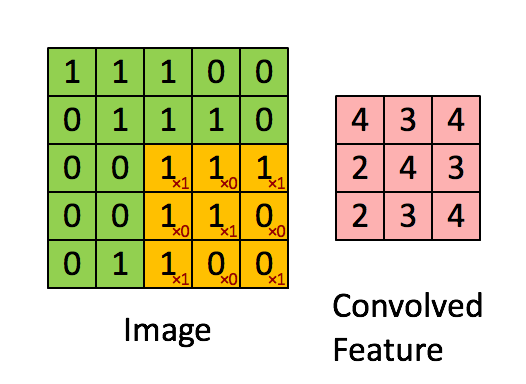
通过非常直观的想想,水平方向的filter就可以表示为: f i l t e r = [ 1 1 1 0 0 0 − 1 − 1 − 1 ] filter\;=\;\begin{bmatrix}1&1&1\\0&0&0\\-1&-1&-1\end{bmatrix} filter=⎣⎡10−110−110−1⎦⎤使用这个filter做上图所示的运算就可以实现水平方面的边沿检测。
进一步想象一下,其实图片识别不就是不断检测边沿吗?通过检测水平边沿,30°方向的边沿,60°方向的边沿等等就可以识别所有边沿,不就是识别图像了吗?在水平方向与竖直方向是比较好确定数值的,但是其他角度的数值如何确定,是否可以通过某种方式让机器自己去学习,这就是CNN的目的。
padding, stride
-
padding
在上图中,原图为 5 × 5 5 \times 5 5×5大小的,filter是 3 × 3 3 \times 3 3×3大小的,得到的结果为 3 × 3 3\times 3 3×3的了。通用地来讲,原图为 n × n n \times n n×n大小的,filter是 f × f f \times f f×f大小的,得到的结果为 ( n − f + 1 ) × ( n − f + 1 ) (n-f+1)\times (n-f+1) (n−f+1)×(n−f+1)的了,这样图片就越来越小了,有时候我们不希望这样,并且这样图片最边沿的信息利用程度降低了。希望边沿信息的利用与中间是同样概率的,输出大小不变化,那么就可以在图片的外围进行扩充,比方说在外围加一圈0,这样filter还是 3 × 3 3 \times 3 3×3大小的化,输出的维度与输入就是一样的。在外围扩充 p p p圈,那么通用地输出维度表达式为 n + 2 p − f + 1 n+2p-f+1 n+2p−f+1。为了保证输出与输入一样, p = f − 1 2 p=\frac{f-1}2 p=2f−1,这解释了为什么f通常都是奇数(并且奇数的话,filter有中心点,更方便理解角度)。
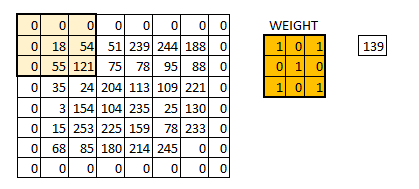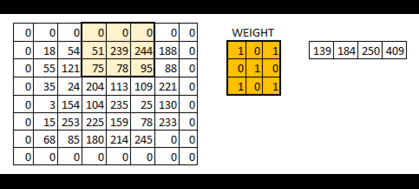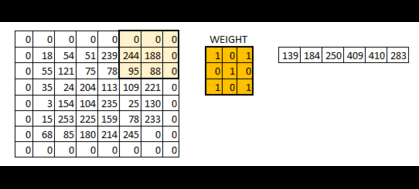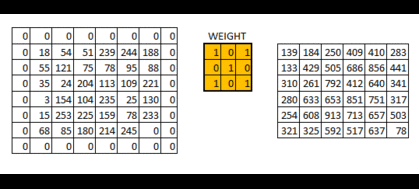
-
stride
在前面都是一步一步移动的,上一步计算的[1:3]的话,下一步就是[2:4],有的时候,觉得这样信息有冗余,跳一跳也没啥的,就是上一步计算[1:3],下一步计算[3:5]就好了。如下图过程。

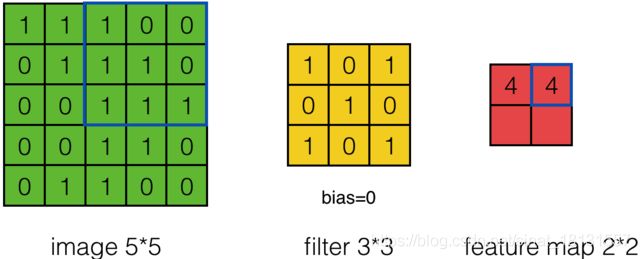

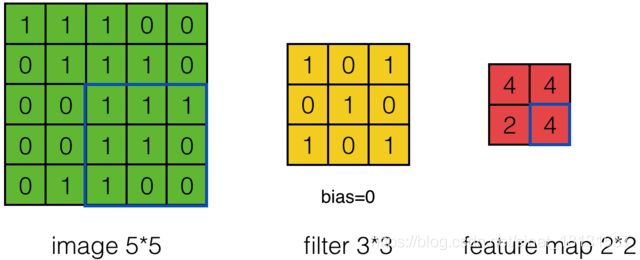
进一步地,输出维度的表达式更新为: n o u t = ⌊ n i n + 2 p a d d i n g − f i l t e r s t r i d e ⌋ + 1 n_{out}=\left\lfloor\frac{n_{in}+2padding-filter}{stride}\right\rfloor+1 nout=⌊stridenin+2padding−filter⌋+1 ⌊ x ⌋ \left\lfloor x\right\rfloor ⌊x⌋表示x向下取整。
三通道(RGB)图片的卷积
上面讨论的可以认为是灰度图像,实际图片有RGB三个通道,那么filter也设定为三个通道,在长/宽/通道三个方向取图像的部分与filter对应元素相乘求和。如下图中,6x6x3的图像,filter是3x3x3,结果为4x4x1的。

输出的第 ( i , j ) (i,j) (i,j)个元素表示为: A i , j = ∑ c = 1 3 ∑ h _ m i n h _ m a x ∑ w _ m i n w _ m a x x h i , w i , c ⋅ f h i , w i , c A_{i,j}=\sum\limits_{c=1}^{3}\sum\limits_{h\_min}^{h\_max}\sum\limits_{w\_min}^{w\_max}x_{h_i,w_i,c}\cdot f_{h_i,w_i,c} Ai,j=c=1∑3h_min∑h_maxw_min∑w_maxxhi,wi,c⋅fhi,wi,c也就是在2D图像的基础上,叠加通道了,filter也要叠加通道,这样可以分别在不同的通道检测边沿。按照前面的理解,这样一个filter可以检测到某个角度的边沿。但是我们通常不只是要检测一个边沿,而是要检测很多,检测一堆边沿。按照上图黄色的一个filter的设计,可以添加多个filter就可以实现多个边沿的检测,如下图中就有2个filter,理论上来讲还可以设置任意多个。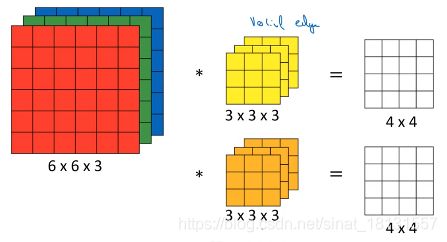
把上图中的两个4x4的输出按照chanel方向堆叠,那么就可以形成一个4x4x2的输出,一般地,有c个filter就能形成c层堆叠。小结一下,源图像的维度为 [ n H , n w , n C ] [n_H,n_w,n_C] [nH,nw,nC],那么filter的维度必定是 [ f , f , n C ] [f,f,n_C] [f,f,nC],他们的通道数一定是一样的,但是可以有 n C ′ n_C' nC′个filter,得到的输出就是 [ n H − f + 1 , n w − f + 1 , n C ′ ] [n_H-f+1,n_w-f+1,n_C'] [nH−f+1,nw−f+1,nC′](假设padding=0,stride=1)
单层CNN
参考一般的神经网络结构, Z [ l ] = W [ l ] A [ l − 1 ] + b [ l ] , A [ l ] = g ( Z [ l ] ) Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]},A^{[l]}=g(Z^{[l]}) Z[l]=W[l]A[l−1]+b[l],A[l]=g(Z[l]),在CNN中,使用filter对输入进行处理后,同样需要使用激活函数,通常使用的激活函数为ReLU并且加偏置b。
符号定义:
| 符号 | 含义 |
|---|---|
| f [ l ] f^{[l]} f[l] | filter size |
| p [ l ] p^{[l]} p[l] | padding |
| s [ l ] s^{[l]} s[l] | stride |
| n C [ l ] n_C^{[l]} nC[l] | number of filters |
| f [ l ] × f [ l ] × n C [ l − 1 ] f^{[l]}\times f^{[l]} \times n_C^{[l-1]} f[l]×f[l]×nC[l−1] | each filter size |
| a [ l ] a^{[l]} a[l] | activation,in dimention of n H [ l ] × n w [ l ] × n C [ l ] n_H^{[l]} \times n_w^{[l]}\times n_C^{[l]} nH[l]×nw[l]×nC[l] |
| A [ l ] A^{[l]} A[l] | activation in batch,in dimention of m × n H [ l ] × n w [ l ] × n C [ l ] m\times n_H^{[l]} \times n_w^{[l]}\times n_C^{[l]} m×nH[l]×nw[l]×nC[l] |
| f [ l ] × f [ l ] × n C [ l − 1 ] × n C [ l ] f^{[l]}\times f^{[l]} \times n_C^{[l-1]}\times n_C^{[l]} f[l]×f[l]×nC[l−1]×nC[l] | weights size |
| 1 × 1 × 1 × n C [ l ] 1 \times 1 \times 1 \times n_C^{[l]} 1×1×1×nC[l] | bias size |
| n H [ l ] n_H^{[l]} nH[l] | n H [ l ] = ⌊ n H [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ n_H^{[l]}=\left\lfloor\frac{n_H^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor nH[l]=⌊s[l]nH[l−1]+2p[l]−f[l]+1⌋ |
| n w [ l ] n_w^{[l]} nw[l] | n w [ l ] = ⌊ n w [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ n_w^{[l]}=\left\lfloor\frac{n_w^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor nw[l]=⌊s[l]nw[l−1]+2p[l]−f[l]+1⌋ |
一张39x39x3的图片有如下处理流程:
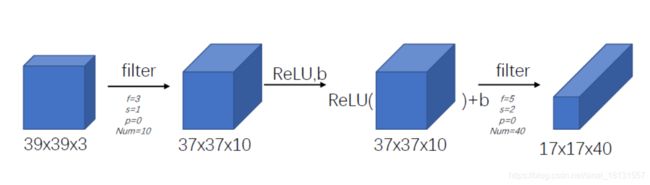
原图经过一层filter处理(f=3,s=1,p=0,num=10)得到的结果为37x37x10的结果,这里的参数有3x3x3x10=270个,ReLU没有参数,但是有10个bias,累计280个参数,第二次filter处理(f=5,s=2,p=0,num=40),结果为17x17x40,参数有5x5x10x40=10000个,累计10280个,如果使用深度神经网络,每层的参数个数是前后层的神经元个数的乘积,是比这个大的。使用CNN对于参数的减少有很大的作用。
其他概念
-
池化(pooling)
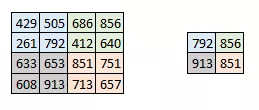
所谓池化就是下采样,信息量比较大,有荣冗余时候,可以通过下采样去掉一部分。有时图像太大,我们需要减少训练参数的数量,它被要求在随后的卷积层之间周期性地引进池化层。池化的唯一目的是减少图像的空间大小。池化在每一个纵深维度上独自完成,因此图像的纵深保持不变。池化层的最常见形式是最大池化。在这里,把步幅定为 2,池化尺寸也为 2。最大化执行也应用在每个卷机输出的深度尺寸中。正如看到的,最大池化操作后,4x4 卷积的输出变成了 2x2。
-
全连接(Fully Connect,FC)
全连接就像是一般的神经网络结构一样,把输入flatten成为一个向量,然后用 Z [ l ] = W [ l ] A [ l − 1 ] + b [ l ] , A [ l ] = g ( Z [ l ] ) Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]},A^{[l]}=g(Z^{[l]}) Z[l]=W[l]A[l−1]+b[l],A[l]=g(Z[l])的方式处理。 -
关于卷积
在数学中,进行矩阵卷积运算(Conv)是将后面一个矩阵翻转180°后在做对应元素相乘,而在CNN中实现的直接对应元素相乘叫做互相关(Cross-correlation)。
CNN网络
找了一个LeNet的结构:
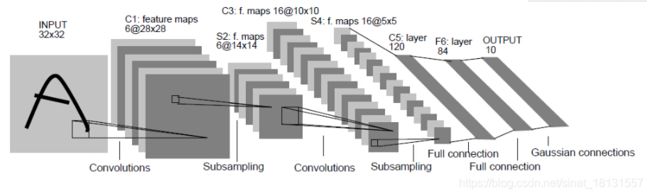
输入为32x32的(黑白图片),使用6个f=5,s=1的filter进行处理,得到了28x28x6的结果,池化(f=2,s=2),结果为14x14x6,使用16个f=5,s=1的filter进行处理,得到结果10x10x16,池化(f=2,s=2),得到结果5x5x16,展开成为400x1的向量,做全连接,输出120x1,再做全连接,输出84x1,继续一次到输出为10x1。
| Activation shape | Activation size | #parameter | |
|---|---|---|---|
| Input | (32,32,1) | 1024 | 0 |
| CONV1(f=5,s=1) | (28,28,6) | 4704 | 208 |
| (avg)POOL1 | (14,14,6) | 1176 | 0 |
| CONV2(f=5,s=1) | (10,10,16) | 1600 | 416 |
| (avg)POOL2 | (5,5,16) | 400 | 0 |
| FC3 | (120,1) | 120 | 48001(=400x120+1) |
| FC4 | (84,1) | 84 | 10081 |
| softmax | (10,1) | 10 | 841 |
可以发现,
- Activation Size总是逐渐变小的;
- 池化层没有参数。
CNN之所以能做到再较少的参数情况下完成这样的任务有两点原因:
- 权重贡献:再一个层的一个filter使用一个权重矩阵对应了整个图片,而这个权重矩阵的尺寸很小。这样的一个好处是CNN对于平移变换不那么敏感。
- 稀疏链接:在每层,输出值只依赖输入的很小一部分。
代码实现
深度卷积网络:实例探究
LeNet-5
参考上一节。参考论文:Gradient-Based Learning Applied to Document Recognition1
输出层原作者使用的Gaussian connections,现在使用较少,使用softmax也是可以的。整个模型只有大约6万个参数。 n H , n w n_H,n_w nH,nw随着过程逐渐变小, n C n_C nC逐渐变大。
AlexNet
参考论文: imagenet classification with deep convolutional neural networks2
AlexNet模型的结构如下图,在前面的描述中,水平向的都是 n w n_w nw方向,在论文的模型中,水平方向是 n C n_C nC方向。
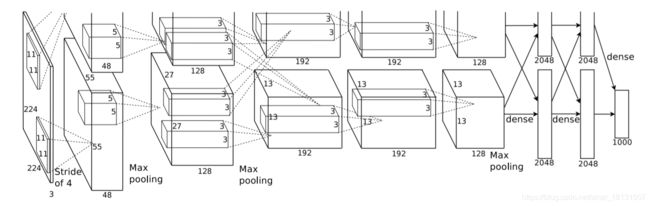
- Input -> CONV1
输入的图片是224x224x3(Andrew说是227x227x3计算的维度更加合理)的,经过一个filter (f=11, s=4)卷积运算,论文还没研究,为了让输出为55x55,padding=2才合理。图中显示的chanel为48,但是有两个GPU在跑,能看到上下两个48,所以是96,下同。 - Max Pooling1
maxpooling1可以看作是filter(f=3,s=2)在不断取最大值运算,这样结果为27x27x96,池化层没有参数。 - CONV2
filter(f=5,s=1,p=2)有256个,输出为27x27x256。课程只介绍了f=5,为了保持输出输入维度相等,s与p自己算的。 - Max Pooling2
filter(f=3,s=2) - CONV3
filter(f=3,s=1,p=1)有384个,same padding,输出为13x13x384。 - CONV4
与CONV3一样的,再实施了一遍。 - CONV5
filter(f=3,s=1,p=1)有256个。 - max pooling5
filter(f=3,s=2) - FC6
将max pooling5输出的9216大小的数据flatten为一个9216x1的向量做全连接,输出层的神经元个数为4096。参数的个数为9216x4096+1=37748737 - FC7
n l − 1 = 4096 , n l = 4096 n_{l-1}=4096,n_l=4096 nl−1=4096,nl=4096 - Output
n l − 1 = 4096 , n l = 1000 n_{l-1}=4096,n_l=1000 nl−1=4096,nl=1000,使用softmax做为激活函数。
| Activation shape | Activation size | #parameter | |
|---|---|---|---|
| Input | (224,224,3) | 150528 | 0 |
| CONV1(f=11,s=4,p=2,num=96) | 55x55x96 | 290400 | 34944(=11x11x3x96+96) |
| POOL1(f=3,s=2) | 27x27x96 | 69984 | 0 |
| CONV2(f=5,s=1,p=2,num=256) | 27x27x256 | 186624 | 614656(=5x5x96x256+256) |
| POOL1(f=3,s=2) | 13x13x256 | 43264 | 0 |
| CONV3(f=3,s=1,p=1,num=384) | 13x13x384 | 64896 | 885020(=3x3x256x384+384) |
| CONV4(f=3,s=1,p=1,num=384) | 13x13x384 | 64896 | 1327488(=3x3x384x384+384) |
| CONV5(f=3,s=1,p=1,num=256) | 13x13x256 | 43264 | 884992(=3x3x384x256+256) |
| POOL5(f=3,s=2) | 6x6x256 | 9216 | 0 |
| FC6( n l − 1 = 9216 , n l = 4096 n_{l-1}=9216,n_l=4096 nl−1=9216,nl=4096) | 4096x1 | 4096 | 37748737(=9216x4096+1) |
| FC7( n l − 1 = 4096 , n l = 4096 n_{l-1}=4096,n_l=4096 nl−1=4096,nl=4096) | 4096x1 | 4096 | 16777217(=4096x4096+1) |
| output( n l − 1 = 4096 , n l = 1000 n_{l-1}=4096,n_l=1000 nl−1=4096,nl=1000) | 1000x1 | 1000 | 4096001(=4096x1000+1) |
AlexNet与LeNet有比较大的相似,但是比LeNet要大很多,LeNet参数约6万个,而AlexNet有6000万个左右。
卷积层中参数要加num是因为AlexNet使用了ReLU作为激活函数。
AlexNet使用了局部响应归一化(local response normalization, LRN),就是在通道方向做归一化,例如得到的结果是13x13x256,就在13x13这个平面上取一个点,然后在通道方向的256个点做归一化处理。(作用不大)
VGG-16
参考论文:VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION3
AlexNet的超参数比较多,f,s,p等。VGG网络参数没那么多,只专注与构建卷积层的简单网络。AlexNet中f=5或f=3等,在VGG中,所有的卷积层CONV(f=3,s=1,p=1),这样卷积后的图片大小不变,MAX-POOL(f=2,s=2)这样图片尺寸变为一半大小。下图是VGG-16的网络结构:

| Activation shape | Activation size | #parameter | |
|---|---|---|---|
| Input | (224,224,3) | 150528 | 0 |
| CONV1 | 224x224x64 | 3211264 | 1792(=3x3x3x64+64) |
| CONV2 | 224x224x64 | 3211264 | 36928(=3x3x64x64+64) |
| POOL2 | 112x112x64 | 802816 | 0 |
| CONV3 | 112x112x128 | 1605632 | 73856(=3x3x64x128+128) |
| CONV4 | 112x112x128 | 1605632 | 147584(=3x3x128x128+128) |
| POOL4 | 56x56x128 | 401408 | 0 |
| CONV5 | 56x56x256 | 802816 | 295168(=3x3x128x256+256) |
| CONV6 | 56x56x256 | 802816 | 590080(=3x3x256x256+256) |
| CONV7 | 56x56x256 | 802816 | 590080(=3x3x256x256+256) |
| POOL7 | 28x28x256 | 200704 | 0 |
| CONV8 | 28x28x512 | 401408 | 1180160(=3x3x256x512+512) |
| CONV9 | 28x28x512 | 401408 | 2359808(=3x3x512x512+512) |
| CONV10 | 28x28x512 | 401408 | 2359808(=3x3x512x512+512) |
| POOL10 | 14x14x512 | 100352 | 0 |
| CONV11 | 14x14x512 | 401408 | 2359808(=3x3x512x512+512) |
| CONV12 | 14x14x512 | 401408 | 2359808(=3x3x512x512+512) |
| CONV13 | 14x14x512 | 401408 | 2359808(=3x3x512x512+512) |
| POOL13 | 7x7x512 | 25088 | 0 |
| FC14 | 4096x1 | 4096 | 102760449(=25088x4096+1) |
| FC15 | 4096x1 | 4096 | 16777217(=4096x4096+1) |
| FC16 | 1000x1 | 1000 | 4096001(=4096x1000+1) |
VGG-16一共有16个卷积层或全连接层,一共有约1.38亿个参数,训练比较麻烦,但是结构非常清晰。
ResNet
参考论文:deep residual learning for image recognition4
非常深的神经网络训练可能会困难,因为梯度下降或者梯度爆炸, 0.9 8 100 = 0.133 0.98^{100}=0.133 0.98100=0.133(0.98的100次方只有0.133了)。**残差神经网络(Residual Network, ResNet)**可以避免这个问题。
常规的神经网络(任意2层)是这样的结构:
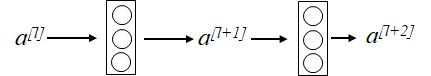
也就是 z [ l + 1 ] = W [ l + 1 ] a [ l ] + b [ l + 1 ] a [ l + 1 ] = g ( z [ l + 1 ] ) z [ l + 2 ] = W [ l + 2 ] a [ l + 1 ] + b [ l + 2 ] a [ l + 2 ] = g ( z [ l + 2 ] ) z^{[l+1]}=W^{[l+1]}a^{[l]}+b^{[l+1]}\\a^{[l+1]}=g(z^{[l+1]})\\z^{[l+2]}=W^{[l+2]}a^{[l+1]}+b^{[l+2]}\\a^{[l+2]}=g(z^{[l+2]}) z[l+1]=W[l+1]a[l]+b[l+1]a[l+1]=g(z[l+1])z[l+2]=W[l+2]a[l+1]+b[l+2]a[l+2]=g(z[l+2])在ResNet中,在进行l+2层的激活时候,不仅只有 z [ l + 2 ] z^{[l+2]} z[l+2],还将 a [ l ] a^{[l]} a[l]也送到这里做激活,也就是上面4个表达式的前3个必变,第4个变成了: a [ l + 2 ] = g ( z [ l + 2 ] + a [ l ] ) a^{[l+2]}=g(z^{[l+2]}+a^{[l]}) a[l+2]=g(z[l+2]+a[l])用图示来表达就是:
或者:
在这两层之间做一个这样的skip connection的操作就是一个Residual Block,把多个块串联起来就是ResNet了。也就是象下图一样,在原本的神经网络之间做一个Residual Block做成ResNet。

在理论上来讲,深度越深,那么模型的效果越好。但是实际中,在深度达到某个值后,就开始变差了,因为参数变得难以训练。在ResNet中,能改善这个问题,随着深度增加,模型效果也越好。
对于某个网络的输出 a [ l ] a^{[l]} a[l](使用的激活函数都是ReLU),还想在他基础上有所提升,那么就在后面再加一个residual block,由前面的公式就有 a [ l + 2 ] = g ( z [ l + 2 ] + a [ l ] ) a^{[l+2]}=g(z^{[l+2]}+a^{[l]}) a[l+2]=g(z[l+2]+a[l]),又有 z [ l + 2 ] = W [ l + 2 ] a [ l + 1 ] + b [ l + 2 ] z^{[l+2]}=W^{[l+2]}a^{[l+1]}+b^{[l+2]} z[l+2]=W[l+2]a[l+1]+b[l+2],所以就有 a [ l + 2 ] = g ( W [ l + 2 ] a [ l + 1 ] + b [ l + 2 ] + a [ l ] ) a^{[l+2]} = g(W^{[l+2]}a^{[l+1]}+b^{[l+2]}+a^{[l]}) a[l+2]=g(W[l+2]a[l+1]+b[l+2]+a[l])在使用L2正则化或者权重衰减,就会压缩W和b的值,如果 W [ l + 2 ] = 0 , b [ l + 2 ] = 0 W^{[l+2]}=0,b^{[l+2]}=0 W[l+2]=0,b[l+2]=0,那么 a [ l + 2 ] = g ( a [ l ] ) = R e L U ( a [ l ] ) = a [ l ] a^{[l+2]}=g(a^{[l]})=ReLU(a^{[l]})=a^{[l]} a[l+2]=g(a[l])=ReLU(a[l])=a[l]。这样的话,虽然加了2层,但是效率并没有变化很多,因为一个恒等变化就是把值复制一次就好,同时,当res block学习到了某些信息有又可以反应在这层的参数中,这样模型就能提升一定性能。
在实际使用中,由于 z [ l + 2 ] , a [ l ] z^{[l+2]},a^{[l]} z[l+2],a[l]需要相加,那么矩阵的大小就要相同,所以在ResNet中通常使用same padding的卷积,如果在应用中确实不一样,那么可以在 a [ l ] a^{[l]} a[l]前面做一个矩阵,让他变换为一样的维度: a [ l + 2 ] = g ( z [ l + 2 ] + W s a [ l ] ) a^{[l+2]}=g(z^{[l+2]}+W_sa^{[l]}) a[l+2]=g(z[l+2]+Wsa[l])
Inception(GooLeNet)
参考论文:Going Deeper with Convolutions5
- 1x1卷积(Network in Network)
1x1的卷积也就是f=1,这样不就是在原数据上乘以一个系数吗?好像并没有什么意义。但是如果数据是 n H × n w × n C n_H \times n_w \times n_C nH×nw×nC,并且 n C ≠ 1 n_C \neq 1 nC=1,那么这样就有意义了,因为使用卷积核做处理时候,需要在三个方向都求和的 ∑ i n H ∑ j n w ∑ k n C s i , j , k f i , j , k \sum\limits_i^{n_H}\sum\limits_j^{n_w}\sum\limits_k^{n_C}s_{i,j,k}f_{i,j,k} i∑nHj∑nwk∑nCsi,j,kfi,j,k,这里 n H = 1 , n w = 1 n_H=1,n_w=1 nH=1,nw=1,所以就是 ∑ k n C s k f k \sum\limits_k^{n_C}s_{k}f_{k} k∑nCskfk。这样就把所有通道方向的数据信息汇总到了一个通道上。按理说1x1卷积说成是1x1xnC卷积的话,更好理解这样操作是有意义的。这样的好处是可以减少/改变通道的数量。比如有一层使用32个1x1x256的卷积核运算,就将通道数由256改变为了32个。
构建卷积网络时候,需要决定卷积核的大小等超参数,要不要添加池化等。而Inception可以帮你决定。比方说,某一层的输出为28x28x192,但是现在不知道应该怎么样继续处理是最好的,那么
- 使用64个1x1的filter处理得到 28x28x64的结果
- 使用128个3x3的filter(p=1,s=1)处理得到的结果为28x28x128
- 使用32个5x5的filter(p=2,s=1)处理得到的结果为28x28x32
- 使用32个maxPOOL(做same padding,使得输入输出的长宽不变)得到的结果为28x28x32(池化后进行1x1的filter卷积)
最后把上面的所有输出在通道方向堆叠起来,也就是结果为28x28x(64+128+32+32)的。这样的好处是,不用管到底是什么方式最好,都给你,你自己去学习参数吧。
这里个问题是参数量问题,计算量太大。比如28x28x192做5x5的卷积输出28x28x32的运算,乘法运算就有:28x28x32x5x5x192=1.2亿。

由另外一种实现方式(上图),在中间添加1x1的filter(16个),输出为28x28x16,乘法运算次数:28x28x16x192=240万,然后28x28x16的结果再做5x5(16)的卷积,乘法运算次数:28x28x32x5x5x16=1000万,一共就是1200万,减少为原来的1/10了。
这个1x1的层被称为瓶颈层(这层的通道数比前后都少)。这就是Inception模块的主要思想。
上面说了5x5filter可以在中间添加1x1的filter减少运算,那么3x3的结构同样可以,1x1的filter就没必要了,已经最简便了。
另外池化层虽然做了same padding长宽没有变化,但是通道也没有变化,为了不让池化的影响太大,需要减小池化的通道数,也可以使用1x1的filter来进行。

那么把输出在通道方向堆叠起来就是一个inception模块:
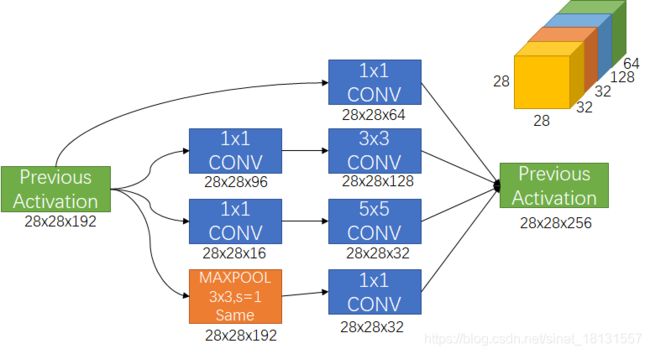
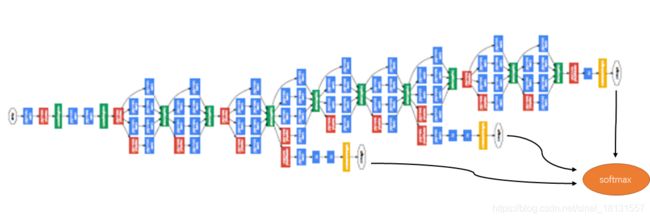
Inception网络就是把很多个这样的模块组合起来了。可以看到在中间某些层的输出也用于最后的输出了,这是Inception的另外一个特点。
迁移学习
迁移学习在之前也有介绍过,在计算机视觉中也可以这样,特别是当自己的数据集比较小时候,可以用别人训练好的模型的前面一部分参数(低级特征),删除最后的输出层设定为自己的。比如使用AlexNet时候,输出是1000的,自己的输出是3分类模型,那就重新设计最后的输出层,保持前面的层结构与(冻结)参数,仅仅训练最后一层就好,这样的好处:
- 利用已经训练好的模型的参数信息
- 节约时间
- 解决数据量小的问题
理论上来讲,数据量很小,那么就只训练最后一层,数据量一般可以训练后面几层,数据量比较大可以训练整个网络。
数据增广(Data augmentation)
数据增广可以提高模型的鲁棒性,可用的方法有:
- 水平镜像(Mirroring)
- 随机剪裁(Random Cropping)
- 图像旋转(Rotation)
- 剪切(Shearing)
- 局部变形(Local Warping)
- color shifting(整体改变RGB通道的值AlexNet中有使用PCA color shifting)
目标检测(Object detection)——YOLO算法
目标检测是不仅仅能识别图片上是什么类型的目标,还能确定这个目标的位置具体在哪里。
目标定位
假设在自动驾驶领域需要做目标检测,首先确定需要检测的目标可能有行人,车辆,摩托车,什么都没有(背景),之前做这样的检测的话,就是一个 4 × 1 4\times 1 4×1的输出就可以了,现在需要把目标的位置也表示出来,所以还需要目标做个框选出来,使用 [ b x , b y , b h , b w ] [b_x,b_y,b_h,b_w] [bx,by,bh,bw]分别表示目标的中心点位置的坐标与高和宽。 y = [ p c b x b y b h b w c 1 c 2 c 3 ] p c 表 示 是 不 是 有 目 标 , 1 为 有 , 0 为 没 有 b x 为 目 标 的 x 坐 标 b y 为 目 标 的 y 坐 标 b h 为 目 标 的 高 度 b w 为 目 标 的 宽 度 c 1 表 示 为 第 一 类 ( 行 人 ) 的 概 率 c 2 表 示 为 第 二 类 ( 汽 车 ) 的 概 率 c 3 表 示 为 第 三 类 ( 摩 托 ) 的 概 率 y=\begin{bmatrix}p_c\\b_x\\b_y\\b_h\\b_w\\c_1\\c_2\\c_3\end{bmatrix}\begin{array}{c}p_c\mathrm{表示是不是有目标},1\mathrm{为有},0\mathrm{为没有}\\b_x\mathrm{为目标的}x\mathrm{坐标}\\b_y\mathrm{为目标的}y\mathrm{坐标}\\b_h\mathrm{为目标的高度}\\b_w\mathrm{为目标的宽度}\\c_1\mathrm{表示为第一类}(\mathrm{行人})\mathrm{的概率}\\c_2\mathrm{表示为第二类}(\mathrm{汽车})\mathrm{的概率}\\c_3\mathrm{表示为第三类}(\mathrm{摩托})\mathrm{的概率}\end{array} y=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡pcbxbybhbwc1c2c3⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤pc表示是不是有目标,1为有,0为没有bx为目标的x坐标by为目标的y坐标bh为目标的高度bw为目标的宽度c1表示为第一类(行人)的概率c2表示为第二类(汽车)的概率c3表示为第三类(摩托)的概率显然当 p c = 0 p_c=0 pc=0时候,目标位置是没有意义的,那么用?表示不关心这里是什么,训练时候的cost可以就只算 y = 1 y=1 y=1的情况。 y ∣ y = 0 = [ 0 ? ? ? ? 0 0 0 ] y|_{y=0}=\begin{bmatrix}0\\?\\?\\?\\?\\0\\0\\0\end{bmatrix} y∣y=0=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡0????000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
滑动窗口目标检测
假设在如下的图片上检测车辆,那么首先有已经把车辆剪到中心的数据集,使用一个固定大小的框去不断截取图片一部分,然后在分割的每个块,使用训练的模型去检测有没有车辆。算法的问题在于如何确定固定窗口的大小?如何选择stride横向/纵向地移动?在不同的应用中可能有不同的选择。并且,这样的方式会大大增加计算量。减少计算量的一种方式就是使用卷积进行滑动窗口检测。

使用卷积的滑动窗口目标检测
- 准备知识——将全连接层转化为卷积层
对于一个CNN-> FC的网络来说,通常结构是类似下图的:

在5x5x16的输出以后,将所有元素全部flatten成为400x1的数据。还有一种方式,使用400个5x5x16的filter进行卷积,这样可以输出1x1x400的矩阵,同样有400个元素。对于第二个全连接层,使用400个1x1x400的filter去卷积得到1x1x400的结果,使用4个1x1的filter得到1x1x4的结果,就实现了使用卷积代替全连接的效果,如下图所示:
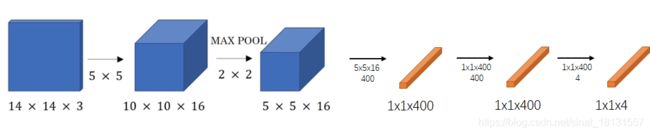
- 卷积实现的滑动窗口
参考论文:OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks6
对于一个14x14的图片进行如下流程处理得到1x1的输出,另外假设在这个14x14的图片的右边和下边各扩充两行数据,同样使用这样的流程就行处理得到的结果为2x2的。进一步看,第一次卷积时候,左上角的处理由于没有受到添加的内容的影响,所以得到的左上角的内容与上图的14x14的内容一样的,只有12x12的后面两行/两列,由于有新的内容作为输入,所以得到的内容也变化了。在2x2的max pooling以后,就只有最后一行。最后一列的内容发生了变化,得到了6x6的结果,在14x14的处理中,这一步的结果是5x5的,为了继续保证整个5x5的内容在6x6的输出中不变化,所以还是使用5x5的卷积进行处理,得到的结果为2x2的,其中1x1的内容还是与上面的一样,新的内容总是出现的1x1以外的2x2结果中。
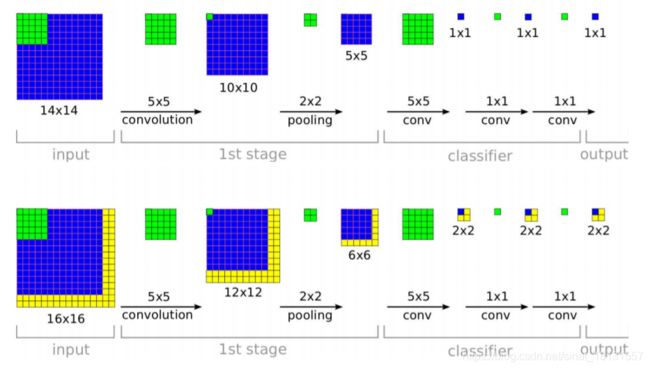
也就是说,使用卷积代替FC的处理,保证了图中任意位置的图像信息也仅仅出现在结果的某一个对应位置。那么这样,把整个图片做卷积,如果遇到需某个部分的结果,就把对应部分的结果在整个大图的结果中找出来就好了。这样很多可以共享的计算就可以避免重复运算了,假设第一次运算的5x5的部分,stride=1,下一次运算时候,有20个点的部分是已经被运算过一次的。
bounding box预测
参考论文:You Only Look Once: Unified, Real-Time Object Detection7
就算是这样,每次用一个框与找图像,不进行重复的卷积运算,但是框的位置可能与图像有一定的差别,造成位置有偏差。那么就需要对图像的位置进行训练与预测。要进行训练的话,就要对数据的标签进行丰富,还是假设需要识别的为行人,汽车,摩托,背景这4类。将一张图片分割为19x19的格子,由于使用卷积代替全连接的话,就可以只做一次卷积,在不同时候将结果内的一部分拿出来用。在图像的所有格子中,都需要做标签。还是用这样的方式表示: y = [ p c b x b y b h b w c 1 c 2 c 3 ] p c 表 示 是 不 是 有 目 标 , 1 为 有 , 0 为 没 有 b x 为 目 标 的 x 坐 标 b y 为 目 标 的 y 坐 标 b h 为 目 标 的 高 度 b w 为 目 标 的 宽 度 c 1 表 示 为 第 一 类 ( 行 人 ) 的 概 率 c 2 表 示 为 第 二 类 ( 汽 车 ) 的 概 率 c 3 表 示 为 第 三 类 ( 摩 托 ) 的 概 率 y=\begin{bmatrix}p_c\\b_x\\b_y\\b_h\\b_w\\c_1\\c_2\\c_3\end{bmatrix}\begin{array}{c}p_c\mathrm{表示是不是有目标},1\mathrm{为有},0\mathrm{为没有}\\b_x\mathrm{为目标的}x\mathrm{坐标}\\b_y\mathrm{为目标的}y\mathrm{坐标}\\b_h\mathrm{为目标的高度}\\b_w\mathrm{为目标的宽度}\\c_1\mathrm{表示为第一类}(\mathrm{行人})\mathrm{的概率}\\c_2\mathrm{表示为第二类}(\mathrm{汽车})\mathrm{的概率}\\c_3\mathrm{表示为第三类}(\mathrm{摩托})\mathrm{的概率}\end{array} y=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡pcbxbybhbwc1c2c3⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤pc表示是不是有目标,1为有,0为没有bx为目标的x坐标by为目标的y坐标bh为目标的高度bw为目标的宽度c1表示为第一类(行人)的概率c2表示为第二类(汽车)的概率c3表示为第三类(摩托)的概率每个格子都是8个参数的输出,那么也就有19x19x8个输出,同样地,数据的标签也要有这么多,也就是说图片需要对每个格子达标签。需要特别说明的是, b x , b y b_x,b_y bx,by表示目标的位置,在一个格子中,左上角的点位置为(0,0),右下级角为(1,1), b x , b y b_x,b_y bx,by是在这个格子内的相对位置点,也就是 0 ⩽ b x < 1 , 0 ⩽ b y < 1 0\leqslant b_x< 1,0\leqslant b_y< 1 0⩽bx<1,0⩽by<1。而 b h , b w b_h,b_w bh,bw表示高和宽,对象可能比一个格子大的,所以 b h , b w b_h,b_w bh,bw可以大于1(都是使用一个格子大小为1,归一化过后的)。如果一个对象出现在多个格子中,那么只认为中心点所在的格子为准,其他格子不认为就对象。
交并比
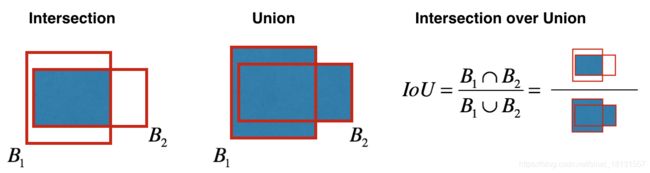
交并比是用来判断一个边界结果预测好坏的数量。假设真实所在位置做一个框是box1,预测的位置的做一个框为box2,那么box1与box2的交集与box1与box2的并集的比值就是交并比。交并比这个参数越大,认为是最合理的位置。
非极大值抑制
我们总是希望找到最好的位置,当一个对象在好几个格子中都检测了,输出一个最合理的位置就行了。也就是说,找到交并比最大的一个,然后,把与整个结果有交集的所有其他结果删除就好了。如下图中没有非极大值抑制时候,可能出现了3个输出,但是实际上是一回事情,那么把这三个的最大交并比输出出来就好了,其他的删除!
Anchor Boxes
如果现在有两个对象同时位于一个格子里面,这样的结果不能用现在的标签表示方法表示出来,那么一个格子中考虑使用两个boxes表示,之前的一个对象有8个参数表示,那么两个就有16(2x8)个参数表示。 y = p c b x b y b h b w c 1 c 2 c 3 } 第 一 个 A n c h o r p c b x b y b h b w c 1 c 2 c 3 } 第 二 个 A n c h o r y=\begin{array}{c}\left.\begin{array}{r}\begin{array}{c}p_c\\b_x\\b_y\\b_h\\b_w\end{array}\\\begin{array}{c}c_1\\c_2\\c_3\end{array}\end{array}\right\}\mathrm{第一个}Anchor\\\left.\begin{array}{r}\begin{array}{c}p_c\\b_x\\b_y\\b_h\\b_w\end{array}\\\begin{array}{c}c_1\\c_2\\c_3\end{array}\end{array}\right\}\mathrm{第二个}Anchor\end{array} y=pcbxbybhbwc1c2c3⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫第一个Anchorpcbxbybhbwc1c2c3⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫第二个Anchor同样还是将图片分为19x19个格子,那么标签就是19x19x2x8大小的。通常Anchor boxes是形状差异比较大的,比如下图的两个,分别用于检测行人和车辆。
这样可以让模型更有针对性。Anchor boxes的形状与数量可以由人工设定,也可以通过k-means的方式自动聚类出来。实际中,通常使用的是
YOLO算法
YOLO就是You Look Only Once的意思。将前面的所有步骤组合起来。
- 将图像分割为19x19的大小
- 对每个格子进行多个Anchor的预测
- 删除 p c p_c pc比较小的(小于0.6)
- 对每类进行非极大值抑制
特殊应用:人脸识别和神经风格转化
人脸识别场景
人脸识别有两种方式:
- verification:验证是不是同一个人
- recongnition:在K个人中找这个人是不是其中一个,是哪一个
人脸识别有个比较大的问题,人的样本通常都在变化,假设一个场景,现在需要给一家公司做人脸识别考勤系统,现在公司只有100个人,所以在做考勤时候,就是拍照了以后在这100个人的数据库中找是不是其中一个或者不是这个公司的人,那么下个月入职了5个人,那这个模型需要重新训练?如果人事变动比较大的话,岂不是无时无刻都在训练,并且新员工来了就只有一张照片,显然是不合理的,这就是需要解决的**一次学习(One-shot learning)**问题。
所谓一次学习问题就是就是一个人通过一个样本就能识别。判断两张图片是不是一个人就是判断他们的相似度,类似 d ( i m g 1 , i m g 2 ) d(img1,img2) d(img1,img2)=degree of difference between images。如果 d ( i m g 1 , i m g 2 ) < τ d(img1,img2)< \tau d(img1,img2)<τ就认为是同一个人,不然就不是同一个人,其中 τ \tau τ是阈值。
Siamese network
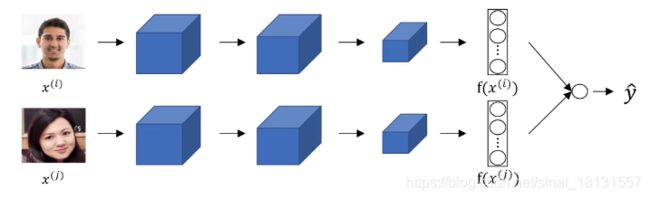
一般的处理图片的神经网络如下,在最后全连接后再用softmax等激活函数进行处理做图片分类。现在在得到下图的最后一层后不再进行softmax输出了。假设最后一层的输出是128x1的,并且记为 f ( x ( 1 ) ) f(x^{(1)}) f(x(1))(可以认为是图片1的一种编码方式),同样的还有另外一张图片的最后一层输出也是128x1的,记为 f ( x ( 2 ) ) f(x^{(2)}) f(x(2))。

那么如果这种编码等能代表图片的话,可以用下式表示相似度8: d ( x ( 1 ) , x ( 2 ) ) = ∣ ∣ f ( x ( 1 ) ) − f ( x ( 2 ) ) ∣ ∣ 2 2 d(x^{(1)},x^{(2)})=||f(x^{(1)})-f(x^{(2)})||_2^2 d(x(1),x(2))=∣∣f(x(1))−f(x(2))∣∣22如果 x ( i ) , x ( j ) x^{(i)},x^{(j)} x(i),x(j)是一个人的照片,那么就是让 ∣ ∣ f ( x ( i ) ) − f ( x ( j ) ) ∣ ∣ 2 2 ||f(x^{(i)})-f(x^{(j)})||_2^2 ∣∣f(x(i))−f(x(j))∣∣22足够小;如果 x ( i ) , x ( j ) x^{(i)},x^{(j)} x(i),x(j)是两个人的照片,那么就是让 ∣ ∣ f ( x ( i ) ) − f ( x ( j ) ) ∣ ∣ 2 2 ||f(x^{(i)})-f(x^{(j)})||_2^2 ∣∣f(x(i))−f(x(j))∣∣22足够大。
三元组损失函数(Triplet loss)
定义:
- Anchor 图片:待识别的图片(A)
- Positive图片:与待处理图片一致的图片(P)
- Negative图片:与待处理图片不一致的图片(N)
以上三张分别就是A/P/N。那么也就是: ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 2 ⩽ ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 2 ||f(A)-f(P)||_2^2 \leqslant ||f(A)-f(N)||_2^2 ∣∣f(A)−f(P)∣∣22⩽∣∣f(A)−f(N)∣∣22左式就是 d ( A , P ) d(A,P) d(A,P),右式就是 d ( A , P ) d(A,P) d(A,P),但是左右都是零的话,上式也是满足的,为了避免输出这个没有用的结果,继续完善方程为: ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 2 − ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 2 + α ⩽ 0 ||f(A)-f(P)||_2^2 - ||f(A)-f(N)||_2^2 +\alpha \leqslant 0 ∣∣f(A)−f(P)∣∣22−∣∣f(A)−f(N)∣∣22+α⩽0这里的 α \alpha α为一个超参数,可以被称作间隔(margin),正常情况下, ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 2 ⩽ ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 2 + α ||f(A)-f(P)||_2^2 \leqslant ||f(A)-f(N)||_2^2+\alpha ∣∣f(A)−f(P)∣∣22⩽∣∣f(A)−f(N)∣∣22+α,也就是说 ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 2 − ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 2 + α ||f(A)-f(P)||_2^2 - ||f(A)-f(N)||_2^2 +\alpha ∣∣f(A)−f(P)∣∣22−∣∣f(A)−f(N)∣∣22+α只要是小于0的就是好的。那么就可以定义三元损失函数为: L ( A , P , N ) = m a x ( ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 2 − ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 2 + α , 0 ) L(A,P,N)=max(||f(A)-f(P)||_2^2 - ||f(A)-f(N)||_2^2 +\alpha, 0) L(A,P,N)=max(∣∣f(A)−f(P)∣∣22−∣∣f(A)−f(N)∣∣22+α,0)只要让损失函数最小即可。有m个样本一起的损失函数记为: J = ∑ i = 1 m L ( A ( i ) , P ( i ) , N ( i ) ) J=\sum\limits_{i=1}^m{L(A^{(i)},P^{(i)},N^{(i)})} J=i=1∑mL(A(i),P(i),N(i))由于训练时候有A图片和P图片,所以训练时候一个人至少需要2张图片。同一个人的照片通常d(A,P)会比d(A,N)要小,所以在训练时候,N图片不是随机选,这样模型学习不到什么有用的信息用于梯度下降。需要尽可能使得d(A,P)与d(A,N)接近使得模型去学习有用信息9。
面部特征与二分类
如果不想做三元组损失,另外一种人脸识别是二分类式的,将全连接的网络,用两个图片去计算编码输出,然后 y ^ = σ ( ∑ k = 1 m w ∣ f ( x k ( i ) ) − f ( x k ( j ) ) ∣ + b ) \hat y=\sigma(\sum\limits_{k=1}^m{w|f(x^{(i)}_k)-f(x^{(j)}_k)|}+b) y^=σ(k=1∑mw∣f(xk(i))−f(xk(j))∣+b)如果是同一个人输出为1,如果不是输出为0。
计算2张图片“距离”的公式除了上式中的表达以外还有: ( f ( x k ( i ) ) − f ( x k ( j ) ) ) 2 f ( x k ( i ) ) + f ( x k ( j ) ) \frac{(f(x^{(i)}_k)-f(x^{(j)}_k))^2}{f(x^{(i)}_k)+f(x^{(j)}_k)} f(xk(i))+f(xk(j))(f(xk(i))−f(xk(j)))2也叫卡方平方公式。
神经风格转化
所谓风格转化就是将一张图片的内容以另外的风格展示出来10,例如:

为了搞清楚怎么进行风格转化的,首先要明白深度神经网络到底都学到了什么东西,假设有如下的网络结构(AlexNet):

那么在第一个隐藏层中取一个单元(遍历了整个训练集),找到最大化激活了这个运算单元的9张图片或者图块,那么在第一层中只能看到图片的一个低等的特征,把这9个图块画出来类似这样的:

那么取不同的单元继续进行这样类似的运算可以得到不同的图块,在9个层中找色块,都以3x3的方式绘制出来11:

那么同理在不同的层也可以这样取色块,看看是怎样的色块最大化地被激活了。可以得到类似这样的结果:

学习到的越来越复杂了。
损失函数(cost function)
生成的图片使用G代替,内容使用C代替,风格使用S代替,
 那么损失函数可以分割为两个部分,一部分是内容的,一部分是风格的,让两个的和达到最小12。 J ( G ) = α J c o n t e n t ( C , G ) + β J s t y l e ( S , G ) J(G)=\alpha J_{content}(C,G)+\beta J_{style}(S,G) J(G)=αJcontent(C,G)+βJstyle(S,G)其中, α , β \alpha,\beta α,β是两个超参数可以调节两部分的比例,或者令 β = 1 − α \beta=1-\alpha β=1−α,这样就只用一个超参数。
那么损失函数可以分割为两个部分,一部分是内容的,一部分是风格的,让两个的和达到最小12。 J ( G ) = α J c o n t e n t ( C , G ) + β J s t y l e ( S , G ) J(G)=\alpha J_{content}(C,G)+\beta J_{style}(S,G) J(G)=αJcontent(C,G)+βJstyle(S,G)其中, α , β \alpha,\beta α,β是两个超参数可以调节两部分的比例,或者令 β = 1 − α \beta=1-\alpha β=1−α,这样就只用一个超参数。
生成的流程为:
首先来计算内容损失函数:
计算内容损失函数 J c o n t e n t ( C , G ) J_{content}(C,G) Jcontent(C,G)通常是在网络的中间找一个层的激活值进行计算,由于在浅层时候,学习到的东西通常为比较简单的元素,而在深层时候元素比较复杂,直观上来讲,我们希望生成的风格转化后的图片,不要太和原图像相似,也不要一点也不像,所以选择中间部分是比较合理的。
使用预训练的卷积网络模型(如VGGNet),计算 a [ l ] ( C ) a^{[l](C)} a[l](C)(原图像在第 l l l层的激活值)与 a [ l ] ( G ) a^{[l](G)} a[l](G)(生成图像在第 l l l层的激活值),如果 a [ l ] ( C ) a^{[l](C)} a[l](C)与 a [ l ] ( G ) a^{[l](G)} a[l](G)是相近的,那么认为两张图片是相近的。 J c o n t e n t ( C , G ) J_{content}(C,G) Jcontent(C,G)表达式可以为 J c o n t e n t ( C , G ) = 1 2 ∣ ∣ a [ l ] ( C ) − a [ l ] ( G ) ∣ ∣ 2 J_{content}(C,G)=\frac12||a^{[l](C)}-a^{[l](G)}||^2 Jcontent(C,G)=21∣∣a[l](C)−a[l](G)∣∣2
那么风格损失函数(style cost function):
进行风格损失函数计算的原文是(视频4.10):Say you are using layer l’s activation to measure the style. Define style as correlation between activation across channels. 怎样理解这里的correlation between activation across channels?
定义 a [ l ] i , j , k a^{[l]_{i,j,k}} a[l]i,j,k表示在第 l l l层时候的 n w n_w nw方向的第 i i i个, n H n_H nH方向的第 j j j个, n C n_C nC方向的第 k k k个元素的数值( a [ l ] a^{[l]} a[l]的维度为 n w × n H × n C n_w\times n_H \times n_C nw×nH×nC)。有 n c [ l ] × n c [ l ] n_c^{[l]}\times n_c^{[l]} nc[l]×nc[l]维度的 G [ l ] G^{[l]} G[l],其中: G k k ′ [ l ] = ∑ i ∑ j a i , j , k [ l ] a i , j , k ′ [ l ] G_{kk'}^{[l]}=\sum\limits_i\sum\limits_j{a_{i,j,k}^{[l]}a_{i,j,k'}^{[l]}} Gkk′[l]=i∑j∑ai,j,k[l]ai,j,k′[l]那么就有: G k k ′ [ l ] ( S ) = ∑ i ∑ j a i , j , k [ l ] ( S ) a i , j , k ′ [ l ] ( S ) G_{kk'}^{[l](S)}=\sum\limits_i\sum\limits_j{a_{i,j,k}^{[l](S)}a_{i,j,k'}^{[l](S)}} Gkk′[l](S)=i∑j∑ai,j,k[l](S)ai,j,k′[l](S)和 G k k ′ [ l ] ( G ) = ∑ i ∑ j a i , j , k [ l ] ( G ) a i , j , k ′ [ l ] ( G ) G_{kk'}^{[l](G)}=\sum\limits_i\sum\limits_j{a_{i,j,k}^{[l](G)}a_{i,j,k'}^{[l](G)}} Gkk′[l](G)=i∑j∑ai,j,k[l](G)ai,j,k′[l](G)如果多个通道描述的特征信息相同(correlation),那么 G k k ′ [ l ] G_{kk'}^{[l]} Gkk′[l]是一个较大的数值,反之是一个较小的数值。风格损失函数可以表述为: J s t y l e [ l ] ( S , G ) = 1 ( 2 n H [ l ] n w [ l ] n C [ l ] ) 2 ∣ ∣ G [ l ] ( S ) − G [ l ] ( G ) ∣ ∣ F 2 = 1 ( 2 n H [ l ] n w [ l ] n C [ l ] ) 2 ∑ k ∑ k ′ ( G k k ′ [ l ] ( S ) − G k k ′ [ l ] ( G ) ) 2 J_{style}^{[l]}(S,G)=\frac1{(2n_H^{[l]}n_w^{[l]}n_C^{[l]})^2}||G^{[l](S)}-G^{[l](G)}||^2_F=\frac1{(2n_H^{[l]}n_w^{[l]}n_C^{[l]})^2}\sum\limits_k\sum\limits_{k'}{(G_{kk'}^{[l](S)}-G_{kk'}^{[l](G)})^2} Jstyle[l](S,G)=(2nH[l]nw[l]nC[l])21∣∣G[l](S)−G[l](G)∣∣F2=(2nH[l]nw[l]nC[l])21k∑k′∑(Gkk′[l](S)−Gkk′[l](G))2其中, ∣ ∣ ⋅ ∣ ∣ F 2 ||·||^2_F ∣∣⋅∣∣F2表示对应元素相减的平方和。系数 1 ( 2 n H [ l ] n w [ l ] n C [ l ] ) 2 \frac1{(2n_H^{[l]}n_w^{[l]}n_C^{[l]})^2} (2nH[l]nw[l]nC[l])21在实际编程中完全可以不用写,因为可以在超参数 β \beta β中包含。并且在实际使用中,如果对多个层都使用风格损失函数结果会更好, J s t y l e ( S , G ) = ∑ l λ [ l ] J s t y l e [ l ] ( S , G ) J_{style}(S,G)=\sum\limits_l\lambda^{[l]}J_{style}^{[l]}(S,G) Jstyle(S,G)=l∑λ[l]Jstyle[l](S,G)其中 λ [ l ] \lambda^{[l]} λ[l]是另外的一组参数。
Gradient-Based Learning Applied to Document Recognition, http://vision.stanford.edu/cs598_spring07/papers/Lecun98.pdf ↩︎
imagenet classification with deep convolutional neural networks, https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf ↩︎
VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION, https://arxiv.org/pdf/1409.1556.pdf ↩︎
deep residual learning for image recognition, https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf ↩︎
Going Deeper with Convolutions, https://www.cs.unc.edu/~wliu/papers/GoogLeNet.pdf ↩︎
OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks, https://arxiv.org/pdf/1312.6229.pdf ↩︎
You Only Look Once: Unified, Real-Time Object Detection, https://pjreddie.com/media/files/papers/yolo.pdf ↩︎
DeepFace: Closing the Gap to Human-Level Performance in Face Verification, https://www.cs.toronto.edu/~ranzato/publications/taigman_cvpr14.pdf ↩︎
FaceNet: A Unified Embedding for Face Recognition and Clustering, https://arxiv.org/pdf/1503.03832.pdf ↩︎
https://cs.stanford.edu/people/jcjohns/ ↩︎
Visualizing and Understanding Convolutional Networks, https://arxiv.org/pdf/1311.2901.pdf ↩︎
A Neural Algorithm of Artistic Style, https://arxiv.org/abs/1508.06576 ↩︎


