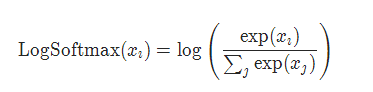pytorch(1)-激活函数sigmoid、损失函数MSE,CrossEntropyLoss,

1.激活函数

全连接网络又叫多层感知器，多层感知器的基本单元神经元是模仿人类神经元兴奋与抑制机制，对其输入进行加权求和，若超过某一阈值则该人工神经元输出为1，否则输出为0。即 原初的激活函数为阶跃函数。由于，sigmoid函数便于求导，便于求导。（因为要优化w,所以要求激活函数应该连续，能够对权重w可求导）。所以实际应用使用的激活函数为sigmoid函数。
小结激活函数的特点： 连续的光滑函数，便于求导。


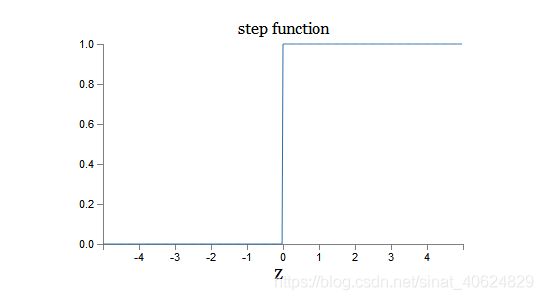
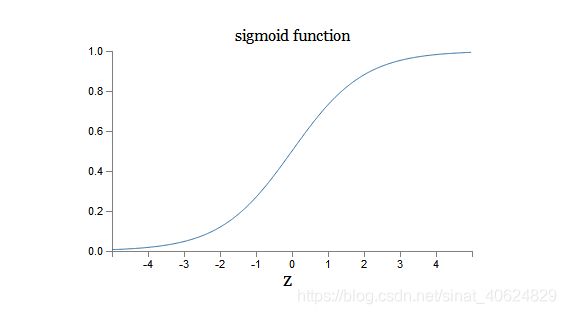
sigmoid函数为阶跃函数的平滑近似。

2.损失函数

神经网络中的损失函数用于衡量网络输出与期望输出的之间的差距。当神经网络用于多类别分类时，网络输出数据与标签一般采用 one-hot向量进行编码。

如神经网络用于MNIST手写数字的识别，每张图片输入网络后，将输出一个10维的向量Y，10维向量的第k维可以看成是该图片是数字k的概率，那么，这张图片最有可能是输出向量的最大维度对应的数字。

损失函数是用于衡量差距的，换一句话说，当网络输出与期望输出越接近时，损失函数值应该越小。并且当网络输出==期望输出时，损失函数应该为0，也就是说，损失函数具有非负性。小结损失函数的两点特性：
(1).网络输出与期望输出越接近时，损失函数值应该越小;
(2)损失函数具有非负性
只要满足以上两点约束的函数都能设计成损失函数，在实际应用中，一个设计良好的损失函数可能会引发一场新的研究热潮。因此，损失函数的设计也是神经网络研究中一块重要的内容。

本文以下总结常用的一些损失函数，并且，附上pytorch相应实例函数。

2.1均方误差损失函数

来自官网的解释：求的是网络输出向量x与目标向量y 之间的均方差，每一维度的求差、求平方、求和、求平均。如果将reduction=‘sum’，那么只到求和，不求平均。

均方误差损失函数使用例子：

loss = nn.MSELoss()
input = torch.randn(3, 10, requires_grad=True)
target = torch.randn(3, 10)
output = loss(input, target)
output.backward()

损失函数输入数据格式要求（3为minibatch的大小）：Input: (3, 10)，Target: (3, 10)
均方差损失函数常用与回归问题，利用神经网络拟合一个复杂函数$f(x)$，网络的最后一层可以依据需要设置不同的激活函数。例如，在输出为一维时，可以直接采用全连接层。

2.2交叉熵损失函数

交叉熵概念源于信息论， 用于衡量估计模型概率分布与真实概率分布之间的差异，随机变量X~p(n)，q(n) 为p(n) 的近似概率分布，则随机变量X与模型 q 之间的交叉熵为：
$$H(X,q)=-\sum _{n}p(n)logq(n)$$
通过数学推导可得,交叉熵=随机变量的熵+真实分布与模型分布的差距：
$$H(X,q)=H(X)+D(p||q)$$

其中，$D(p||q)$为相对熵，$H(X)$为随机变量的熵。因为，在同一随机变量的前提下（H(X)相同），真实分布与模型分布的差距（即相对熵$D(p||q)$）越小，则交熵越小。也就是说， 交叉熵满足 损失函数的两条特性。所以可以采用交叉熵作为损失函数。

交叉熵衡量的是两个两个概率分布之间的差距，所以，全连接网络的最后一层输出应该采用softmax() 函数，将输出转化为概率分布；期望输出（标签向量）采用onehot编码。网络最后一层的加权输出向量$x$通过$softmax()$激活后得到输出分布向量z：
$$z_k=softmax(x{)}_k=\frac{e^{x_k}}{{\sum }_i{e}^{x_i}}$$
计算网络输出与目标输出之间的交叉熵
$$Loss(z,label)=H(z,label)=-log\frac{e^{x_j}}{{\sum }_i{e}^{x_i}}$$
其中，$j$为l$label$中为1 的维度，也就是，待检测目标所属的类别。

因为，上面两个式子可以化简，直接取最后的结果:

$$Loss(x,label)=-log\frac{e^{x_j}}{{\sum }_i{e}^{x_i}}$$

(本文最重要的事情)
所以，在pytorch 中CrossEntropyLoss() 函数的输入为：最后一层全连接的加权输出向量（不经过softmax()激活），和期望输出的onehot编码中为1的位置（类别标号，是一个标量，如手写数字识别，真实数字8的标号为7）。如果是批次数据，那就是每个数据交叉熵的求和求均值。

简单的例子：手写数字识别问题（1,2,3），网络输出采用的one-hot 编码，实际上是一个概率分布。即给定一张数字为1的图像，经过神经网络处理过后，最期待网络输出的应该是：[1,0,0]。也就是说图片为1的概率为1：$p(图片为1)=1$，$p(图片为2)=0$，$p(图片为3)=0$。但网络实际输出[0.5,0.2,0.3]（也应该是一个概率分布），也就是说$q(图片为1)=0.5$，$q(图片为2)=0.2$，$q(图片为3)=0.3$。依据公式计算交叉熵。

交叉差熵损失函数使用例子：

loss = nn.CrossEntropyLoss()
input = torch.randn(3, 10), requires_grad=True) #minibatch=3，即3行，每一行为一个10维向量
target = torch.empty(3, dtype=torch.long).random_(10) # 1行，3列，每一列的数字为0-10之间的整数
output = loss(input, target)
output.backward()

2.3 NLLLoss()

同时，pytorch 还提供了nn.LogSoftmax()与NLLLoss()的组合，实现交叉熵损失函数。此时，网络的最后一层加权输出，要经过nn.LogSoftmax()进行激活；
NLLLoss()使用例子：

m = nn.LogSoftmax(dim=1)
loss = nn.NLLLoss()
#input is of size N x C = 3 x 5
input = torch.randn(3, 5, requires_grad=True)
#each element in target has to have 0 <= value < C
target = torch.tensor([1, 0, 4])
output = loss(m(input), target)
output.backward()

2.4 BCELoss()

pytorch 提供了二元交叉熵损失函数，用于处理二分类问题。
简单情况：单个样本时，最后一层网络输出应该为概率值，表示这个样本是一个类别的概率。因此，最后一层的输出应为sigmoid()[sigmoid()函数与概率对应关系再论]。因此这个网络输出与目标输出之间的交叉熵为：
$$l_n=-(y_{n}log{x}_n+(1-y_n)log(1-x_n))$$
$y_n$为第n 个样本为真的概率，$x_n$第n 个样本为真的网络输出概率。在实际二分类问题中，y_n为0或者1(标签设置准则)。

官网文档连接（英文）：https://pytorch.org/docs/stable/nn.html