机器学习--降维技术PCA
1.PCA降维原理:
PCA属于线性降维方式:
X为原空间 W为变化矩阵 Z为新空间 Z的维数要小于X维数,实现了降维处理。
用一个超平面来表示正交属性空间的样本点,这个超平面应该尽量满足最近重构性以及最大可分性,即空间中所有点离这个超平面尽可能近,样本点在超平面的投影尽可能区分开,基于最近重构性以及最大可分性,可以推导出PCA分析就是对于矩阵XXT进行特征值分解:
对于XXT特征值分解之后,将特征值排序,取前d`特征值对应的特征向量即为变换矩阵W
PCA第一个主成分选取数据差异性最大的方向,第二个主成分与第一个方向正交并且数据差异性次大的的方向,依次选取d`个主成分。
算法流程如下所示: 样本矩阵进行中心化 计算协方差矩阵XXT,对协方差矩阵进行特征值分解,前d`大的特征值对应的特征向量组成变换矩阵W
2.PCA实现:
代码如下:
def pca(dataMat, topNfeat=9999999):
meanVals = mean(dataMat, axis=0)
meanRemoved = dataMat - meanVals #remove mean
covMat = cov(meanRemoved, rowvar=0)
eigVals,eigVects = linalg.eig(mat(covMat))
eigValInd = argsort(eigVals) #sort, sort goes smallest to largest
eigValInd = eigValInd[:-(topNfeat+1):-1] #cut off unwanted dimensions
redEigVects = eigVects[:,eigValInd] #reorganize eig vects largest to smallest
lowDDataMat = meanRemoved * redEigVects#transform data into new dimensions
reconMat = (lowDDataMat * redEigVects.T) + meanVals
return lowDDataMat, reconMatmean方法 axis = 0:压缩行,对各列求均值,返回 1* n 矩阵 求各列的平均值
meanRemoved = dataMat - meanVals 中心化
covMat = cov(meanRemoved, rowvar=0) 如果rowvar为True(默认值),则每行代表一个变量,并在列中显示(即每一列为一个样本)。 否则,关系被转置:每列代表变量,而行包含观察值。
eigVals,eigVects = linalg.eig(mat(covMat)) 进行特征值分解,返回特征值以及特征向量
eigValInd = argsort(eigVals) #sort, sort goes smallest to largest
eigValInd = eigValInd[:-(topNfeat+1):-1] #cut off unwanted dimensions
redEigVects = eigVects[:,eigValInd] #reorganize eig vects largest to smallest
将特征值有小到大排序,取最后几个,以及对应的特征向量组成变换矩阵redEigVects
lowDDataMat = meanRemoved * redEigVects#transform data into new dimensions 得到降维后的数据
reconMat = (lowDDataMat * redEigVects.T) + meanVals 重构原数据
加载数据集:
def loadDataSet(fileName, delim='\t'):
fr = open(fileName)
stringArr = [line.strip().split(delim) for line in fr.readlines()]
datArr = [list(map(float,line)) for line in stringArr]
return mat(datArr)
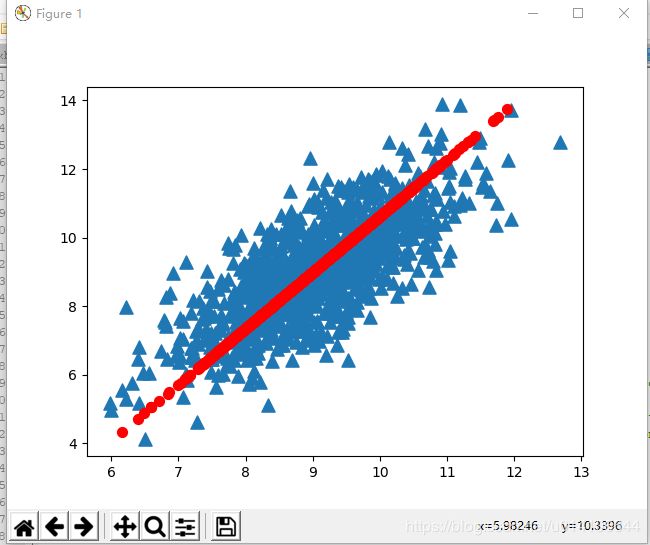
输入数据样本为二维数据,左边为进行第一主成分分析后,重构后的新数据,可知数据沿方差最大方向;右边为第一,第二主成分分析后重构数据,发现数据并没有损失,因为本来数据集就是二维数据。
半导体制造数据PCA降维分析:
数据样本:
数据中缺失数据的处理: 由于未知数据缺失处的含义,用0来代替不妥,可以使用非零的均值来代替缺失处数据。
求出第i列中非NAN数据的均值 将第i列中NAN处数值换成均值
def replaceNanWithMean():
datMat = loadDataSet('secom.data', ' ')
numFeat = shape(datMat)[1]
for i in range(numFeat):
meanVal = mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i]) #values that are not NaN (a number)
datMat[nonzero(isnan(datMat[:,i].A))[0],i] = meanVal #set NaN values to mean
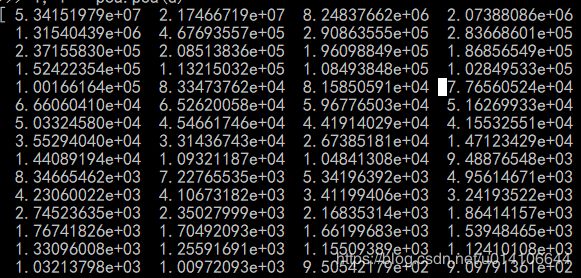
return datMat观察矩阵特征值分解的特征值如下:
可知数据的主要成分集中在前几个特征值,可以通过不断测试选取不同的特征值来测试方差百分比以及累计方差百分比来决定特征向量的个数,依次来包含数据的绝大部分信息。