贝塞尔曲线学习以及在Android中的使用
贝塞尔曲线介绍
贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。
贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。
贝塞尔曲线为计算机矢量图形学奠定了基础。它的主要意义在于无论是直线或曲线都能在数学上予以描述。
贝塞尔曲线是从起始点P0开始，在控制点的控制下，根据t值的变化而变化，最终到达终点PN之后的路径，改变控制点的位置会影响最后曲线的形状，其中t的值为0~1，可以把t当作百分比来理解。
贝塞尔曲线公式推导
一阶贝塞尔曲线
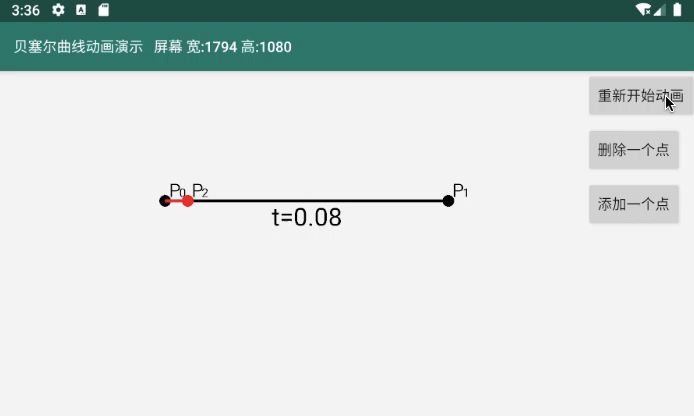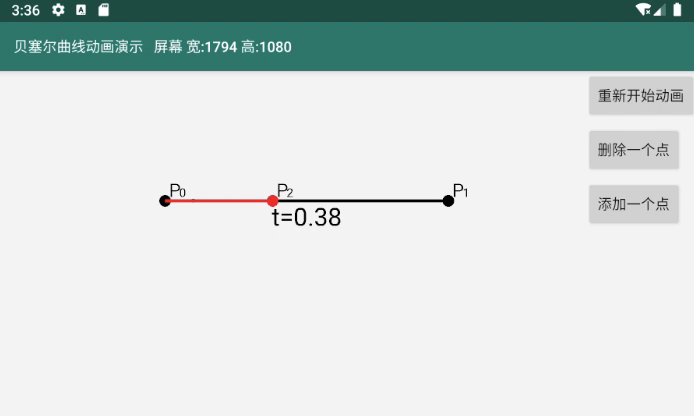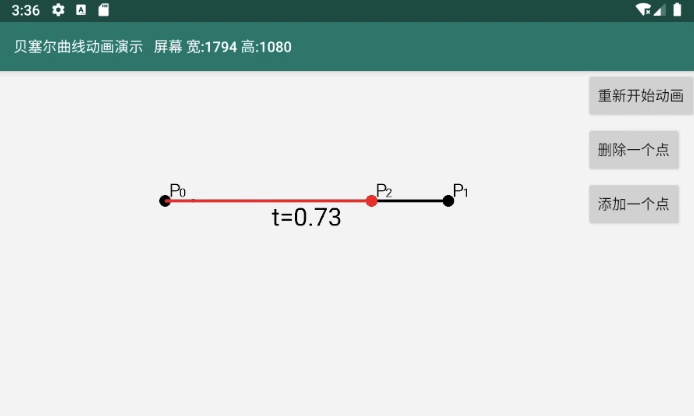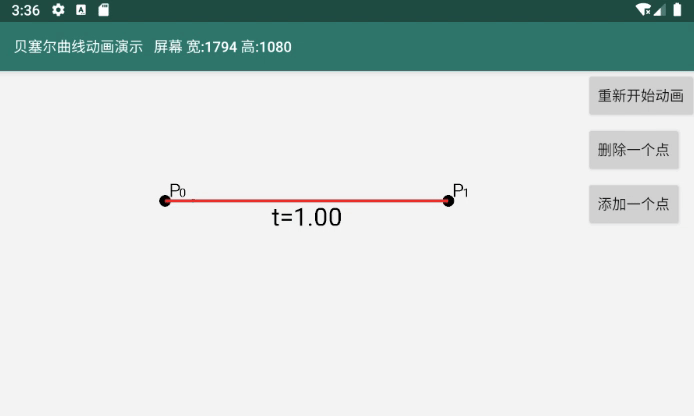
图中红色的线就是一阶贝塞尔曲线。
一阶贝塞尔曲线最开始只有开始点P0和结束点P1，没有控制点，所以是一条直线
红色的线由点P2动态移动得来，P2跟随着t的变化(从0过渡到1)而变化。我把P2这样的点成为贝塞尔曲线点
P2变化的规则是 线P0P2 = 线P0P1 * t ，这是线P0P2长度的计算结果，但是点P2的位置是P0的位置加上线P0P2长度才对。
即
将P2替换成函数B(t)来表达得出，一阶贝塞尔曲线一般公式是：
二阶贝塞尔曲线
图中红色的曲线既是二阶贝塞尔曲线的一种
它的绘制过程有 P0 ~ P5 6个点参与，
最原始的点有三个 P0 ~ P2，P0是开始点，P2是结束点，P1是控制点
P3 ~ P5是P0 ~ P2根据t的变化动态生成的点。
P3 是 P0，P1两个点的一阶贝塞尔曲线点
P4 是 P1，P2两个点的一阶贝塞尔曲线点
P5 是 P3，P4两个点的一阶贝塞尔曲线点
在绘制过程中有三个层的变化过程，第一层，也是最外层的黑色线段，是由初始的点P0，P1，P2按照顺序依次连接而成，然后在第一层的基础上，分别取第一层的两点之间的一阶贝塞尔曲线点，从而生成了第二层的两个点P3，P4，也就是绿色的线段，然后再取第二层的两个点的一阶贝塞尔曲线点，生成了最后的贝塞尔曲线的点P5，最后绘制整个P5的运动轨迹即可得到P0，P1，P2这三个点的二阶贝塞尔曲线。
P5是最终的贝塞尔曲线点，它是P3，P4的一阶贝塞尔曲线，带入一阶贝塞尔曲线公式，可得
P5 = (1-t)P3 + t*P4
同理P3 = (1-t)P0 + t*P1 P4 = (1-t)P1 +t*P2
将P3，P4的等式代入导P5的计算式中可得
--->先替换P3
--->然后替换P4
--->展开等式
将P5用函数B(t)代替可得二阶贝塞尔曲线通用公式
三阶贝塞尔曲线
图中红色的曲线就是三阶贝塞尔曲线的一种
共有10个点参与绘制，第一层黑色线段 P0-P1-P2-P3，第一层时原始给出的点，后面的点都是根据第一层生成的，第二层绿色线段P4-P5-P6，第三层蓝色线段P7-P8，最后一层红色曲线是P9动态划过的轨迹，也就是贝塞尔曲线。
在随着t逐渐变化的过程中，除了最外层的点，每个点与它所关联的点相差了几层，那这个点就是它所关联的点几阶贝塞尔曲线，所谓的”关联“就是，这个点所在的线段，以及所在线段的点所在的线段，以此类推。例如P7与P4、P5这两个点相差一层，是他们的一阶贝塞尔曲线，与P0、P1、P2这三个点相差两层，是他们的二阶贝塞尔曲线。这个规律适用于更高阶的贝塞尔曲线。贝塞尔曲线是逐层取一阶贝塞尔曲线计算而得。
三阶贝塞尔曲线的通用公式是
这个公式也可以按照二阶的通用公式的推导方法而来。
四阶与五阶贝塞尔曲线展示
通用公式
如果从一阶开始罗列出几个公式，就可以总结一个通用的公式。
给定点P0、P1、…、Pn，其贝塞尔曲线即：
对公式 
前两个部分进行一下说明，后面的部分都比较容易理解
表示对i 从0开始到n 有 n个式子，对所有式子的结果进行求和，式子计算的规则就是在它后面的表达式
这个参数是一个系数，它的计算方法是 
即 n的阶乘除以，i的阶乘与n-i的阶乘之和，例如对于 n = 5，i = 3 计算的的结果是，
如果利用这个公式计算四阶公式，可以得出：
如何在安卓中使用贝塞尔曲线
经过上面的动画展示可以看到贝塞尔是一个可控制的平滑的曲线，那么怎么在安卓中使用呢。
上面的公式每个点只有一个参数参与计算，实际上点是由两个参数X，Y组成，那在使用公式时，分别对所有点计算X的贝塞尔曲线，然后在对所有的点计算Y的贝塞尔曲线，最后(X,Y)这个点就是贝塞尔点了。
在Android的绘制线可以使用Path类，在Path类中对二阶和三阶贝塞尔曲线做了封装，省去了手写公式的时间。这两种贝塞尔曲线比较常用，能满足大多数开发上的需求，如下
//二阶贝赛尔曲线绘制方法
public void quadTo(float x1, float y1, float x2, float y2)
public void rQuadTo(float dx1, float dy1, float dx2, float dy2)
//三阶贝赛尔曲线绘制方法
public void cubicTo(float x1, float y1, float x2, float y2,float x3, float y3)
public void rCubicTo(float x1, float y1, float x2, float y2,float x3, float y3)quadTo是二阶贝塞尔曲线，二阶贝塞尔曲线应该有三个点，但是参数中却给了两个点，这两个点中，第一个是控制点，最后一个是结束点，而开始点就是，Path.moveTo到的那个点或者没有moveTo，那就是原始坐标点。
rQuadTo方法与quadTo一样，绘制了二阶贝塞尔曲线，不同点是，rQuadTo的起始点使用了上一次曲线的终点。而quadTo的起始点只是Path.moveTo的点
例如下面代码
Path path = new Path();
path.moveTo(100,100);
path.quadTo(200,200,300,100);
path.rQuadTo(100,100,200,0);//第一次rQuadTo
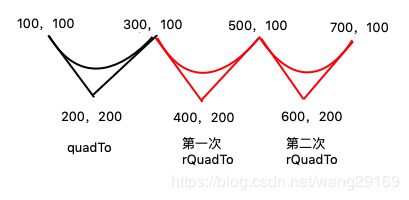
path.rQuadTo(100,100,200,0);//第二次rQuadTo实际的情况如下图所示
最开始调用的是quadTo方法，绘制完成后Path的终点是(300,100)，紧接着调用第一次rQuadTo，那么它会以上一次绘制的终点，也就是在点(300,100)的基础之上加上现在的所有的点的坐标，x都加上300，y都加上100， 即path.rQuadTo(100,100,200,0) 等同于，Path先moveTo(300,100),然后在quadTo(100+300,100+100,200+300,0+100)，即quadTo(400,200,500,100)
然后第二次调用rQuadTo(100,100,200,0)这个时候上一次绘制的终点变成了第一次rQuadTo的终点，也就是(500,100)，要在此基础之上加上现在的所有的点的坐标，x都加上500，y都加上100，即rQuadTo(100,100,200,0)等同于，Path先moveTo(500,100),然后再quadTo(100+500.100+100,200+500,0+100)，即quadTo(600,200,700,100);
最后绘制的线如下图的曲线部分所示
rCubicTo的含义与rQuadTo类似，都是参照之前绘制的终点加上现在的坐标然后进行绘制
水波纹效果能量球的实现
1. 先画出水波纹
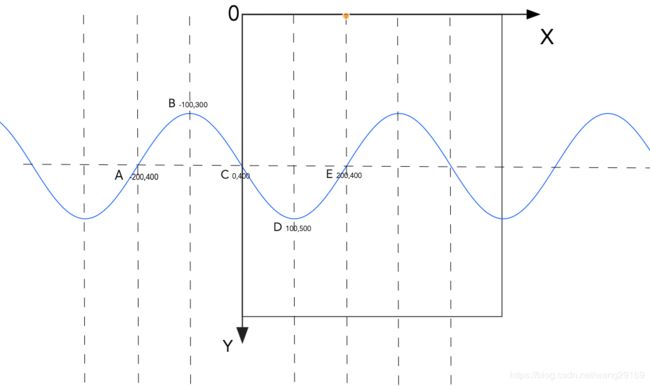
按照下图，矩形代表手机屏幕，画一个波浪线，它由多个贝塞尔曲线首尾相接组成，整个波浪线从A点开始绘制
图中A,B,C,D四个点组成了两个贝塞尔曲线，每个贝塞尔曲线横坐标方向的长度都是200，一个是 ABC三个点组成的，另一个一个是CDE三个点组成的，这两个贝塞尔曲线的形状是一样的，只不过后者是前者的倒影，两个贝塞尔曲线组成一组，每一组的形状都是一样的，一组水平长度总共是400，然后再水平方向向右再绘制几组超过右侧屏幕即可，这样先把波浪线绘制完成，然后让它水平循环向右运动，就可以实现动态水波纹的效果。
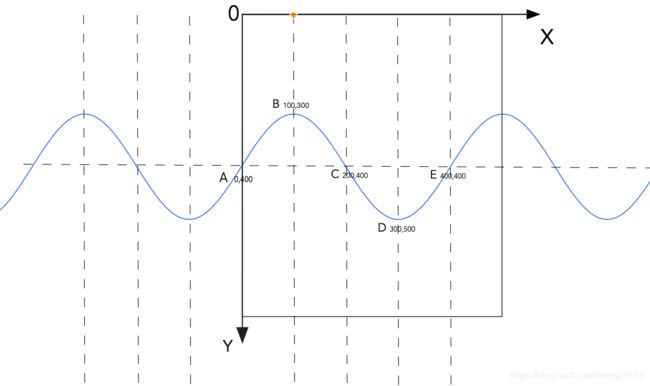
下图表示整个波浪线向右运动了200个单位
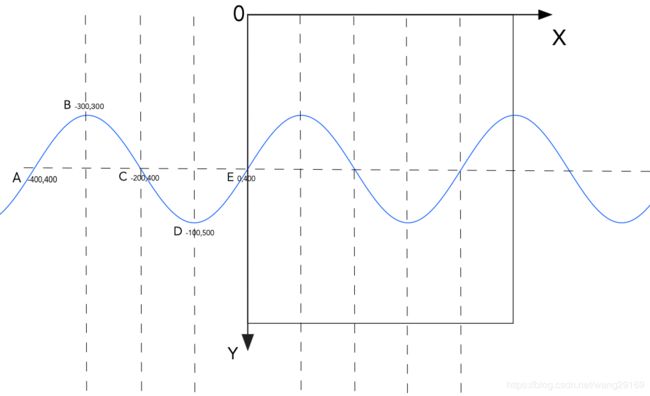
如果整个波浪线向右运动了两个贝塞尔曲线的长度，也就是一组的长度后，整个波浪线的起始点A即将进入屏幕，如下图所示，如果再向右运动那么起始点A就进入了屏幕，曲线左边就会出现空白，这个时候让A点回到最初的位置重新绘制曲线，然后继续下一次的动画，这样就能实现循环的水波纹绘制了。
其实这个波浪线也可以用多阶的贝塞尔曲线来完成，如果用三阶的贝塞尔曲线，以图中的例子，就是用A、B、D、E，这四个点来完成，A作为开始点，E作为结束点，然后B、D作为控制点。绘制几个这样的三阶贝塞尔曲线首尾相接即可。除了三阶的之外还可以用更高阶的贝塞尔曲线完成，这只需要多设置几个控制点，做好前后衔接就行。
下面看下代码的实现
由于水波纹是首尾相接的多个贝塞尔曲线构成，那么可以设置好Path的起点，然后调用rQuadTo方法传入每个控制点的坐标与之前的坐标的相对位置即可，这样起点变化后，后续的控制点也会跟着变化。
实现这个效果，需要自定义View，创建一个类继承View类，重写onDraw方法即可
先做设置成员变量
int startX = -400;
int startY = 400;
Path bezierPath = new Path();
Paint paint = new Paint();
然后初始化
paint.setColor(Color.BLACK);
paint.setStyle(Paint.Style.STROKE);
paint.setStrokeWidth(10);onDraw方法
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
bezierPath.reset();
//先让Path移动到起始点，A
bezierPath.moveTo(startX,startY);
// 绘制贝塞尔曲线ABC
// 然后参照A点，设置偏移的大小，B点相对A点偏移(100,-100),C点相对A点偏移(200,0)
bezierPath.rQuadTo(100,-100,200,0);
// 绘制贝塞尔曲线CDE
// 这次的起点是上一次绘制的终点，也就是C点
// D点相对C点偏移(100,100) E点相对C点偏移(200,0)
bezierPath.rQuadTo(100,100,200,0);
// 绘制下一组贝塞尔曲线，过程和第一组一致
bezierPath.rQuadTo(100,-100,200,0);
bezierPath.rQuadTo(100,100,200,0);
bezierPath.rQuadTo(100,-100,200,0);
bezierPath.rQuadTo(100,100,200,0);
bezierPath.rQuadTo(100,-100,200,0);
bezierPath.rQuadTo(100,100,200,0);
//开始绘制水波纹Path
canvas.drawPath(bezierPath,paint);
//设置x水平向右移动，垂直方向不动
startX+=20;
//如果起始点到达屏幕左侧，就从初始位置开始绘制
if (startX>=0){
startX = -400;
}
//重绘
invalidate();
}每次绘制完成之后，起始点X的坐标就向右移动，然后下一次绘制的波浪线就会跟着向右，达到水波纹动画的效果
看下效果
好吧，看起来稍微有点奇怪，这可能是曲线的高度有点高，然后长度也不够长导致的，调整一下参数试试，起点X修改为-800
int startX = -800;
int startY = 400;onDraw()方法
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
bezierPath.reset();
bezierPath.moveTo(startX,startY);
bezierPath.rQuadTo(200,-50,400,0);
bezierPath.rQuadTo(200,+50,400,0);
bezierPath.rQuadTo(200,-50,400,0);
bezierPath.rQuadTo(200,+50,400,0);
bezierPath.rQuadTo(200,-50,400,0);
bezierPath.rQuadTo(200,+50,400,0);
canvas.drawPath(bezierPath,paint);
startX+=20;
if (startX>=0){
startX = -800;
}
invalidate();
}每个贝塞尔曲线的长度加长一点，变成了400，这样每一组的长度就有800，所以起点的X坐标设置成了-800,贝塞尔曲线的高度也从100降低到了50，
变化的有些缓慢，调整一下X坐标每次改变的大小即可
这次感觉有点像了。
2. 实现水波纹上升
现在只是有了水波纹的效果，但是水波纹能量球是从底向上一点点增大的，那么让Y坐标也跟着变试试。
首先在onLayout中获取控件的高度
@Override
protected void onLayout(boolean changed, int left, int top, int right, int bottom) {
super.onLayout(changed, left, top, right, bottom);
//从底向上升
startY = getMeasuredHeight();
}然后在onDraw方法中设置高度每次绘制都减少1
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
bezierPath.reset();
bezierPath.moveTo(startX,startY);
bezierPath.rQuadTo(200,-50,400,0);
bezierPath.rQuadTo(200,+50,400,0);
bezierPath.rQuadTo(200,-50,400,0);
bezierPath.rQuadTo(200,+50,400,0);
bezierPath.rQuadTo(200,-50,400,0);
bezierPath.rQuadTo(200,+50,400,0);
canvas.drawPath(bezierPath,paint);
startX+=20;
if (startX>=0){
startX = -800;
}
if (startY>0){
//从底部开始向上升
startY --;
invalidate();
}
}看下效果
水波纹上升的有些缓慢。需要增大Y减少的幅度
3. 绘制能量球
最后一步是绘制球形，其实就是绘制一个圆形，然后把水波纹绘制成实心再加上颜色即可。
这个需要用到Canvas的clipPath方法，从View中割出一个圆形来，调用这个方法之后，该控件只显示被剪裁的部分，canvas其他的不可见，这样就实现了能量球的绘制。
先添加圆形路径，然后在onLayout方法中设置path为圆形
float halfX = (int) (getMeasuredWidth() / 2f);
int halfY = (int) (getMeasuredHeight() / 2f);
//设置一个圆形路径
circlePath.addCircle(halfX, halfY, Math.min(halfX, halfY), Path.Direction.CW);
然后在onDraw方法最开始的位置添加切割圆形的代码，并绘制圆形
//切割一个圆形
canvas.clipPath(circlePath);
//绘制圆形
canvas.drawPath(circlePath, circlePaint);
最后的效果如下
OK，整个水波纹能量球就绘制完成了，下面是全部代码
package com.wx.beziercurvestudy;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.util.AttributeSet;
import android.view.View;
/**
* 绘制水波纹能量球
*/
public class BezierWaterRippleView extends View {
/**
* X起始点
*/
public static final int START_X = -800;
/**
* X每次减少的步长
*/
public static final int X_STEP = 20;
/**
* Y每次减少的步长
*/
public static final int Y_STEP = 5;
public static final int BEZIER_LENGTH = 200;
public static final int BEZIER_HEIGHT = -50;
Path circlePath = new Path();
Paint circlePaint = new Paint();
int startX = START_X;
int startY = 0;
Path bezierPath = new Path();
Paint bezierPaint = new Paint();
public BezierWaterRippleView(Context context) {
this(context, null);
}
public BezierWaterRippleView(Context context, AttributeSet attrs) {
this(context, attrs, 0);
}
public BezierWaterRippleView(Context context, AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
circlePaint.setColor(Color.BLACK);
circlePaint.setStrokeWidth(5);
circlePaint.setStyle(Paint.Style.STROKE);
bezierPaint.setColor(Color.BLUE);
bezierPaint.setStyle(Paint.Style.FILL);
bezierPaint.setStrokeWidth(10);
}
@Override
protected void onLayout(boolean changed, int left, int top, int right, int bottom) {
super.onLayout(changed, left, top, right, bottom);
float halfX = (int) (getMeasuredWidth() / 2f);
int halfY = (int) (getMeasuredHeight() / 2f);
//设置一个圆形路径
circlePath.addCircle(halfX, halfY, Math.min(halfX, halfY), Path.Direction.CW);
//从底向上升
startY = getMeasuredHeight();
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//切割一个圆形
canvas.clipPath(circlePath);
//绘制圆形
canvas.drawPath(circlePath, circlePaint);
bezierPath.reset();
//设置起点
bezierPath.moveTo(startX, startY);
//设置贝塞尔曲线路径
bezierPath.rQuadTo(BEZIER_LENGTH, -BEZIER_HEIGHT, BEZIER_LENGTH * 2, 0);
bezierPath.rQuadTo(BEZIER_LENGTH, BEZIER_HEIGHT, BEZIER_LENGTH * 2, 0);
bezierPath.rQuadTo(BEZIER_LENGTH, -BEZIER_HEIGHT, BEZIER_LENGTH * 2, 0);
bezierPath.rQuadTo(BEZIER_LENGTH, BEZIER_HEIGHT, BEZIER_LENGTH * 2, 0);
bezierPath.rQuadTo(BEZIER_LENGTH, -BEZIER_HEIGHT, BEZIER_LENGTH * 2, 0);
bezierPath.rQuadTo(BEZIER_LENGTH, BEZIER_HEIGHT, BEZIER_LENGTH * 2, 0);
//下面三行代码设置封闭的形状，绘制水波纹下面的阴影部分。
//右下角
bezierPath.lineTo(getMeasuredWidth(), getMeasuredHeight());
//左下角
bezierPath.lineTo(0, getMeasuredHeight());
//起点
bezierPath.lineTo(startX, startY);
bezierPath.close();
//绘制贝塞尔曲线
canvas.drawPath(bezierPath, bezierPaint);
//垂直方向开始移动
if (startY > 0) {
//水平向右移动
startX += X_STEP;
//到达屏幕最左侧时，重新回到水平方向的起点
if (startX >= 0) {
startX = START_X;
}
startY -= Y_STEP;
invalidate();
}
}
/**
* 重新绘制
*/
public void reDraw() {
startX = START_X;
startY = getMeasuredHeight();
invalidate();
}
}
安卓中只封装了常见的二阶和三阶的绘制，对于多阶的曲线，可以手动操作Path类，将t从0到1变化过程中的点的集合通过公式求得，然后依次添加到Path中，再绘制即可，例如四阶的实现方式如下:
public void setFourthBezierCurvePath(Point P0, Point P1, Point P2, Point P3, Point P4, Path path) {
int num = 0;
for (int i = 0; i < 100; i++) {
int t = (int) (num / 100f);
float subT = 1 - t;
//带入四阶公式进行计算
int bezierX = (int) (P0.x * subT * subT * subT * subT
+ 4 * P1.x * subT * subT * subT * t
+ 6 * P2.x * subT * subT * t * t
+ 4 * P3.x * subT * t * t * t
+ P4.x * t * t * t * t);
int bezierY = (int) (P0.y * subT * subT * subT * subT
+ 4 * P1.y * subT * subT * subT * t
+ 6 * P2.y * subT * subT * t * t
+ 4 * P3.y * subT * t * t * t
+ P4.y * t * t * t * t);
//记录当前t值下的贝塞尔曲线点
path.lineTo(bezierX,bezierY);
num++;
}
}给Path设置好之后，就可以使用Canvas进行绘制，即可得到对应的贝塞尔曲线。
贝塞尔曲线可以实现很多特效，只要涉及到路径动态变化，都可以考虑使用它，例如简单的翻页效果，QQ上面的移除未读消息角标的轨迹等等。只要我们预先设计好曲线的轨迹，就可以实现炫酷的动效。
参考资料
百度百科-贝塞尔曲线
n阶bezier曲线 通用公式说明和应用 - 杂七杂八
n 阶贝塞尔曲线计算公式实现 - Duan的博客
Android自定义View——贝塞尔曲线实现水波纹效果
canvas进阶之贝塞尔公式推导与物体跟随复杂曲线的轨迹运动
Android自定义View（四） Path之贝塞尔曲线