Python中的函数和作用域
Python中的函数和作用域
1. 函数
1.1 函数的简介
当我们在重复使用某一功能时,我们可能会写很多重复的代码,例如我们求圆的周长,当圆的直径改变时,是不是我们又要重新写一遍计算过程呢?如果涉及到很复杂的过程,而下次使用仅仅改变参数,那么我们还有必要重复这一过程吗?
这时我们可以利用函数来解决这一问题。一个功能就像黑盒一样,我们不需要知道它是怎么工作的,我们只要知道接口(输入,输出)即可使用。
例如Python的内置函数print我们只要知道它需要我们提供哪些参数,以及它会给我们怎样的输出即可。这就是所谓的抽象,我们不知道工作原理,但也能使用它。所以我们可以写一个函数(黑盒),设置直径为输入,周长为输出,当函数写好后,我们只要输入直径即可,不用考虑函数内部是如何计算的,我们得到输出后,继续做我们想做的事情。
当我们想做一道菜时,有人负责洗菜,有人切菜,有人炒菜,将这些人的工作合在一起,就完成了做菜这个任务,这就是分解的思想,我们将这个任务看成是函数,许多函数在一起完成了一件比较大的事情。
可以简单理解一块可重复使用的代码,我们称之为函数(function),当我们调用函数时,这个函数才会执行。
1.2 函数的特征
- 名称
- 参数 (0 或 多个)
- 有docstring (可选,但是建议有,注释的意思)
- 函数体
- 返回一些值
以下是定义一个函数简单的例子,注意函数内要有四个空格的缩进,如果没有返回值的话,会默认返回None:
#def是用来定义函数的关键字
#is_even是函数的名称
#i是参数(参数可以是任何类型)
#三个引号括起来的是docstring
#docstring下面的语句是函数体
#return后的是返回值
def is_even( i ):
"""
Input: i是一个正的int类型
Returns True 如果 i 是偶数, 否则返回 False
"""
print("inside is_even")
return i%2 == 0
#调用函数,并用a接收返回值
a = is_even(2)
print(a)
2. 作用域
2.1 形参和实参
首先我们先不涉及编程。高中的函数y = f(x),这个x就相当于是形参,指一种抽象,将我们用f(3)的时候,这个3就是实参了,就是实际我们使用的值,形参和实参大致就是这个意思,不要搞混了。例如:
def f( x ):#x是形参
x = x + 1
print('in f(x): x =', x)
return x
#以下是调用函数
x = 3#初始化x
z = f( x )#调用函数,传入实参,将返回值给z
2.2 函数作用域
利用pythontutor网站对代码的执行进行可视化,我把所有步骤都截了下来,先看图,右侧反映了变量的变化情况。
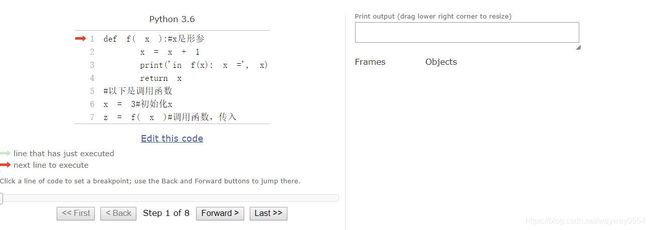

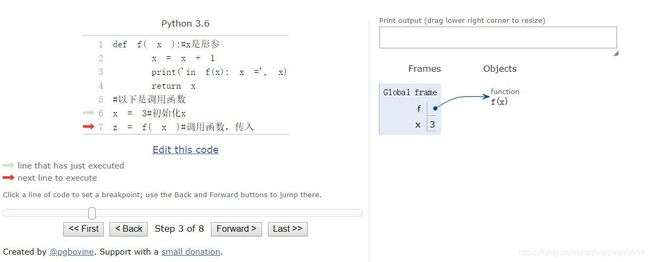
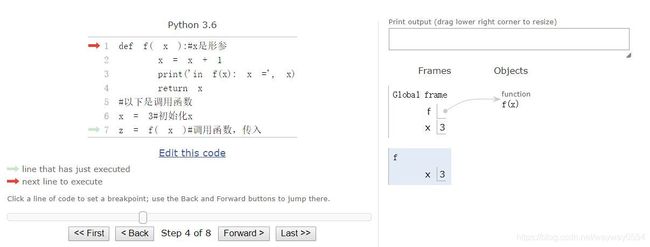

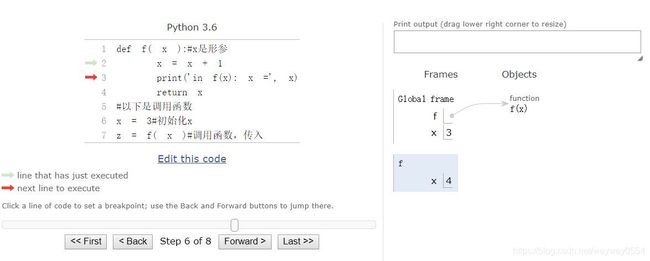


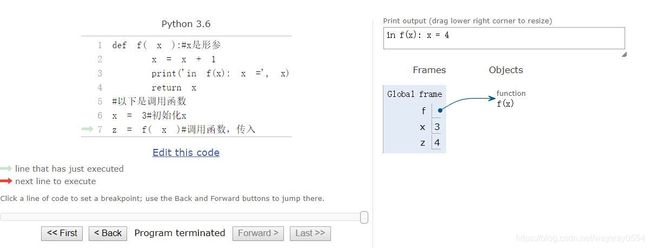
可以看到函数内是一个作用域,外面是访问不到的(一般情况)。当进入一个函数时,一个新的作用域就被创建了。函数内的x和外面的x不是一个x,x是不可变量,这和之后的list等数据类型不一样,之后再说。
- 函数里可以访问外面的变量
- 函数里不可以修改外部定义的变量
以下是是几个例子,如果有不清楚,可以进入 www.pythontutor.com(我推荐的代码可视化网站)中尝试运行。
第一个例子,在外边定义了一个x,但是在f内又定义了一个x,这两个x不是一个x,函数内部使用的x是函数内部定义的。
def f(y):
x = 1
x += 1
print(x)
x = 5
f(x)
print(x)
第二个例子,在g中使用的x是外部定义的x
def g(y):
print(x)
print(x + 1)
x = 5
g(x)
print(x)
第三个例子,会报错,不能在内部修改外部的值,UnboundLocalError: local variable 'x' referenced before assignment
def h(y):
x += 1
x = 5
h(x)
print(x)
3. 参考
参考了Mit 6.0001的课件