数据结构与算法（七）动态规划（dp算法）实战

今天轮到dp算法实战了。首先要自我实现0-1背包问题，然后是LeetCode #132。

0-1背包问题

关于背包问题，其实可以分为两种类型：0-1背包问题 和 部分背包问题。

1. 先通过一个例子来说明一下二者的区别吧！

有一个窃贼在偷窃一家商店时发现有n件物品，第i件物品价值为vi元，重量为wi，假设vi和wi都为整数。他希望带走的东西越值钱越好，但他的背包中之多只能装下W磅的东西，W为一整数。他应该带走哪几样东西？

• 0-1背包问题：每件物品或被带走，或被留下，（需要做出0-1选择）。小偷不能只带走某个物品的一部分或带走两次以上同一个物品。
• 部分背包问题：小偷可以只带走某个物品的一部分，不必做出0-1选择。

更通俗点理解，0-1背包问题的一件物品可以想象成是一个金锭；而部分背包问题中的一件物品可以想象成是金粉。

2. 这两个问题的解决策略也是不同的。

关于0-1背包问题，采用的是动态规划的解决方法；而部分背包问题采用的是贪心法。

• 0-1背包问题：

在选择是否要把一个物品加到背包中，必须把该物品加进去的子问题的解与不取该物品的子问题的解进行比较。这种方式形成的问题导致了许多重叠子问题，满足动态规划的特征。

• 部分背包问题：

总是选择每一磅价值 (Vi / Wi) 最大的物品添加进背包中。那么其解决过程是：对每磅价值进行排序，依次从大到小选择添加进背包中。

拓展阅读：动态规划 之 0-1背包问题（虽然是用C++实现的，推荐看一下伪代码和优化后的伪代码）

拓展阅读2：贪心算法之背包问题 （今天我们不研究部分背包问题，有时间看一下）

我们在第五节已经看过0-1背包问题的图解，不了解的可以直接看这里----->动态规划 - 图解

那么填入的原则为：

table[i][j]= max(table[i-1][j],当前商品的价值+剩余空间价值(table[i-1][j-当前商品重量])）

注：如果处于特殊位置，如table[0][0]单元格，没有table[i-1][j]那么就是0

使用第五节例子中的变量：

#使用第五节的变量
import numpy as np
# 定义重量
weight = {}
weight["water"] = 3
weight["book"] = 1
weight["food"] = 2
weight["jacket"] = 2
weight["camera"] = 1
# 定义价值
worth = {}
worth["water"] = 10
worth["book"] = 3
worth["food"] = 9
worth["jacket"] = 5
worth["camera"] = 6

# 存放行标对应的物品名:
table_name = {}
table_name[0] = "water"
table_name[1] = "book"
table_name[2] = "food"
table_name[3] = "jacket"
table_name[4] = "camera"

pack = 6

# 创建矩阵,用来保存价值表
table = np.zeros((len(weight), pack))

# 创建矩阵，用来保存每个单元格中的价值是如何得到的（物品名）
table_class = np.zeros((len(weight), pack), dtype=np.dtype((np.str_, 500)))

for i in range(len(weight)):
    for j in range(pack):
        real = j + 1
        this_weight = weight[table_name[i]]
        this_worth = worth[table_name[i]]
        before_worth = table[i - 1, j]
        q = table[i - 1, j - this_weight]
        if i == 0:
            if this_weight <= real:
                table[i, j] = this_worth
                table_class[i,j] = table_name[i]
        else:
            if real == this_weight:
                q = 0
            if real < this_weight:
                q = -this_worth
            table[i, j] = max(before_worth, this_worth + q)

            if table[i, j] == before_worth:
            	table_class[i,j] = table_class[i-1,j]
            elif q == 0:
            	table_class[i,j] = table_name[i]
            else:
            	table_class[i,j] = table_name[i] + "," + table_class[i - 1, j - this_weight]

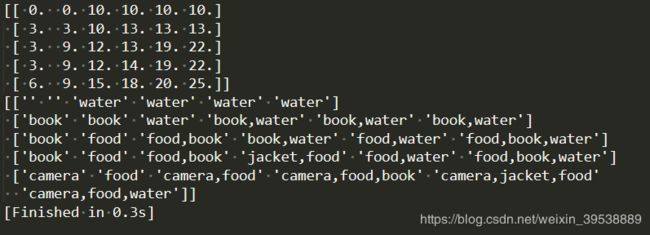
print(table)
print(table_class)

还是需要多练，“明白意思”和“自己能写”真是两回事儿

废了九牛二虎之力才出结果

LeetCode实战

132. Palindrome Partitioning II

https://leetcode.com/problems/palindrome-partitioning-ii/

将给定的字符串，以最小的cut数，切割成回文，即从左往右读和从右往左读内容一致

拓展阅读1：维基百科 - 回文

拓展阅读2：维基百科 - 回文数

因为明天有考试，今天要复习一些内容，所以先粘贴一个Discuss的结果，明天考试回来再细细琢磨

class Solution(object):
    def minCut(self, s):
        
        ## at cut[i] indicates the number of minimum cuts of s[i:j)
        cut = [-1] + [x for x in range(len(s))]
        
        dp = [[False] * (len(s)+1) for _ in range(len(s)+1)]
        
        
        for length in range(len(s)):
            for start in range(len(s) - length):
                end = start + length
                if length == 0: dp[start][end] = True
                elif length == 1: dp[start][end] = s[start] == s[end]
                else: dp[start][end] = dp[start+1][end-1] and s[start] == s[end]
        
        for i in range(len(s)+1):
            for j in range(i):
                if dp[j][i-1]: 
                    cut[i] = min(cut[i],cut[j]+1)
        return cut[-1]

写在最后

一周编程训练营到这里就要接近尾声了，首先想感谢Datawhale平台，以这种近乎不要钱的方式，为我们提供学习计划和老师，真的是非常感谢。祝愿Datawhale平台越办越好！

其次想感谢群里付出的各位助教，每天不求回报激励着我们前行，非常感谢！

拿了几次全场最佳，感谢我的奖惩助教-孙超，谢谢你对我的认可！

肯定不能忘了感谢04号 - 枣子姐姐，感谢你每天对我的点评！祝愿你顺利毕业，找到自己心仪的工作。还有，公众号要坚持下去哦！

2019年，以训练营充实的学习生活开了一个好头，希望自己后面继续坚持下去。

七天的时间过的真的很快，对于算法的学习也仅仅是一个开始，后期打算把《图解算法》这本书完整的看一遍，然后多做实战题来提高自己的编程水平。

经过这七天的学习，看了太多的博客，感觉每天写博客的水平都在提高，希望接下来可以多多记录下自己的学习轨迹，把自己学到的感悟到的分享给大家。

下次见